11.6: Delocalized Electrons: Bonding in the Benzene Molecule

Learning Objectives

• To be able to explain how mixing atomic orbitals make molecule orbitals with delocalized bonding

The advantage of MO theory becomes more apparent when we think about \(\pi\) bonds, especially in those situations where two or more \(\pi\) bonds are able to interact with one another. Let’s first consider the \(\pi\) bond in ethene from an MO theory standpoint (in this example we will be disregarding the various sigma bonds, and thinking only about the \(\pi\) bond). According to MO theory, the two atomic 2p_z orbitals combine to form two \(\pi\) molecular orbitals, one a low-energy π bonding orbital and one a high-energy π-star (π*) antibonding molecular orbital. These are sometimes denoted in molecular diagrams with the Greek letter psi (Ψ) instead of π (Figure \(\PageIndex{1}\)).

Figure \(\PageIndex{1}\): Mixing of adjacent p atomic orbitals results in the bonding (\(\pi\)) and anti-bonding (\(\pi^*\)) molecular orbitals.

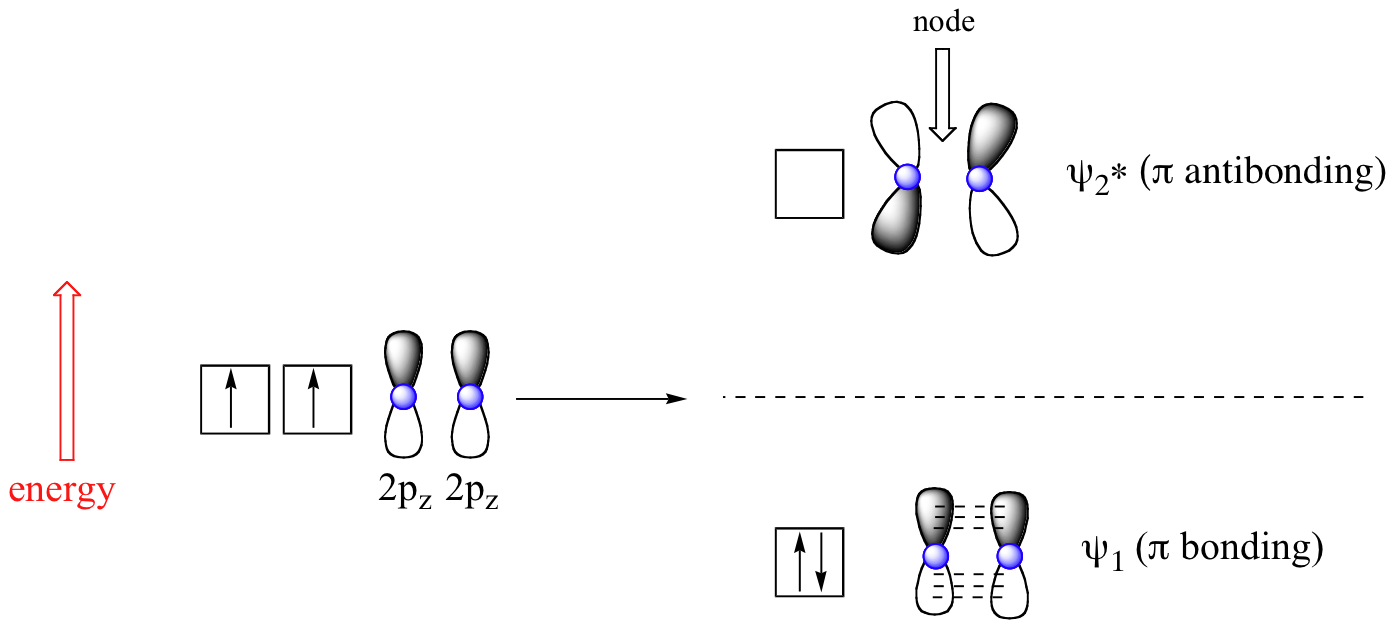
In the bonding Ψ₁ orbital, the two shaded lobes of the 2p_z orbitals interact constructively with each other, as do the two unshaded lobes (remember, the shading choice represents mathematical (+) and (-) signs for the wavefunction). Therefore, there is increased electron density between the nuclei in the molecular orbital – this is why it is a bonding orbital. In the higher-energy antibonding Ψ₂* orbital, the shaded lobe of one 2p_z orbital interacts destructively with the unshaded lobe of the second 2p_z orbital, leading to a node between the two nuclei and overall repulsion.

By the aufbau principle, the two electrons from the two atomic orbitals will be paired in the lower-energy Ψ₁ orbital when the molecule is in the ground state (Figure \(\PageIndex{1}\)).

Now, consider the 1,3-butadiene molecule. From valence orbital theory we might expect that the C₂-C₃ bond in this molecule, because it is a \(\sigma\) bond that would rotate freely.

Figure \(\PageIndex{2}\): The "single bond" in the 1,3-butadiene molecule is expected to rotate just like all sigma bonds.

However, it is experimentally found that there are significant barriers to rotation about this bond (as well as about the C₁-C₂ and C₃-C₄ double bonds), and that the entire molecule is planar. It is also observed that the C₂-C₃ bond, while longer than the C₁-C₂ and C₃-C₄ double bonds, is significantly shorter than a typical carbon-carbon single bond.

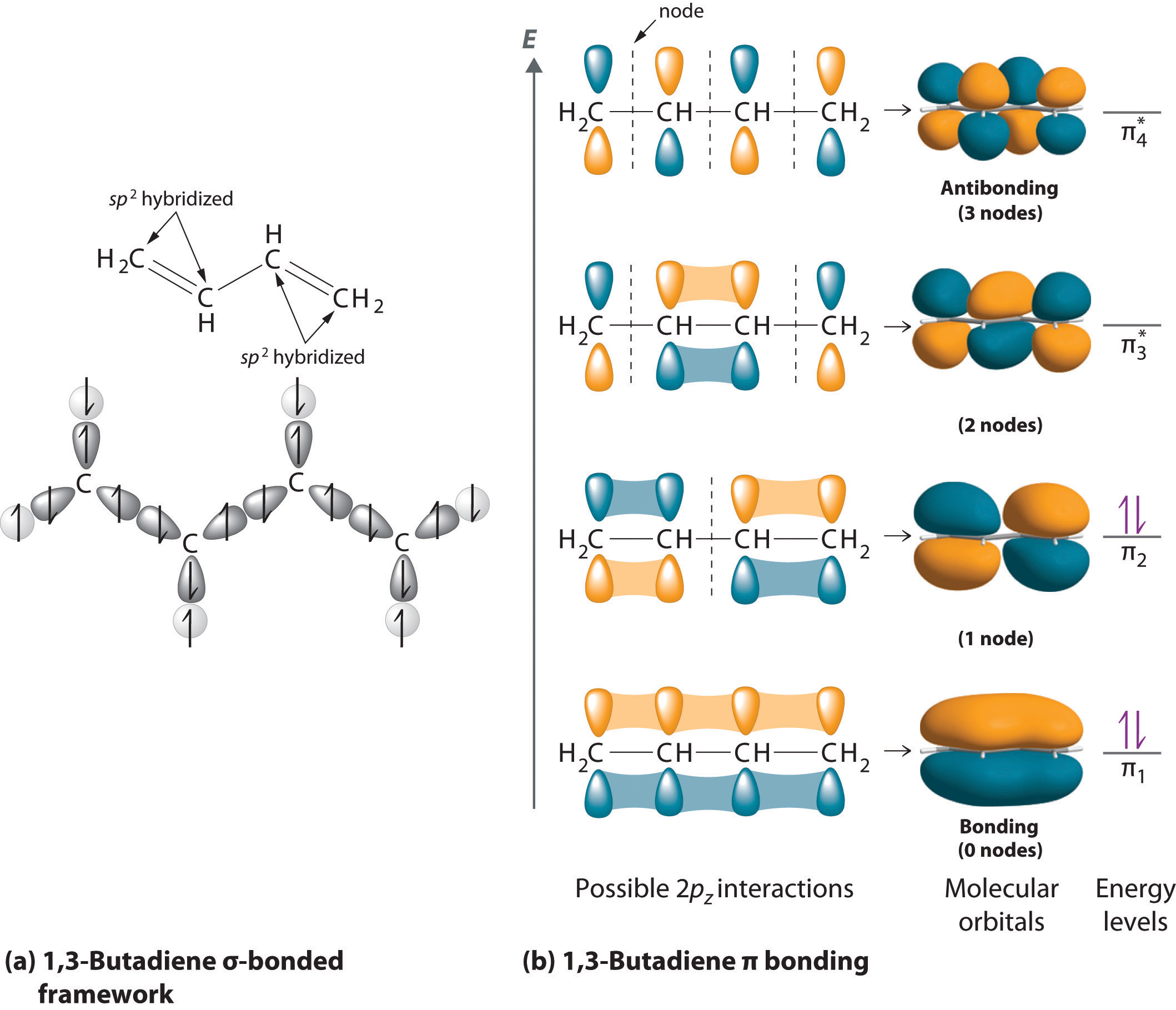
Molecular orbital theory accounts for these observations with the concept of delocalized π bonds. In this picture, the four 2p_z orbitals are all parallel to each other (and perpendicular to the plane of the \(\sigma\) bonds), and thus there is \(\pi\)-overlap not just between C₁ and C₂ and C₃ and C₄, but between C₂ and C₃ as well. The four atomic (2p_z) orbitals have combined to form four \(\pi\) molecular orbitals.

Figure \(\PageIndex{3}\): Molecular orbitals expected for mixing of the perpendicular p atomic orbitals of the 1,3-butadiene molecule.

The lowest energy molecular orbital, Ψ₁, has zero nodes, and is a bonding MO. Slightly higher in energy, but still lower than the isolated p orbitals, is the Ψ₂ orbital. This orbital has one node between C₂ and C₃, but is still a bonding orbital due to the two constructive interactions between C₁-C₂ and C₃-C₄. The two higher-energy MO’s are denoted Ψ₃* and Ψ₄*, and are antibonding. Notice that Ψ₃* has two nodes and one constructive interaction, while Ψ₄* has three nodes and zero constructive interactions. The energy of both of these antibonding molecular orbitals is higher than that of the 2p_z atomic orbitals of which they are composed.

By the aufbau principle, the four electrons from the isolated 2p_z atomic orbitals are placed in the bonding Ψ₁and Ψ₂ MO’s. Because Ψ₁includes constructive interaction between C₂ and C₃, there is a degree, in the 1,3-butadiene molecule, of π-bonding interaction between these two carbons, which accounts for the shorter length and the barrier to rotation. The simple Lewis structure picture of 1,3-butadiene shows the two π bonds as being isolated from one another, with each pair of π electrons ‘stuck’ in its own π bond. However, molecular orbital theory predicts (accurately) that the four π electrons are to some extent delocalized, or ‘spread out’, over the whole π system.

Figure \(\PageIndex{3}\): The atomic orbitals that combine to generate the lowest energy molecular orbital in the 1,3-butadiene molecule.

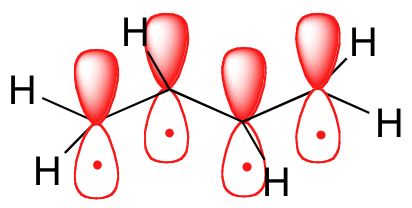
1,3-butadiene is the simplest example of a system of ‘conjugated’ π bonds. To be considered conjugated, two or more π bonds must be separated by only one single bond – in other words, there cannot be an intervening sp³-hybridized carbon, because this would break up the overlapping system of parallel 2p_z orbitals.

Benzene

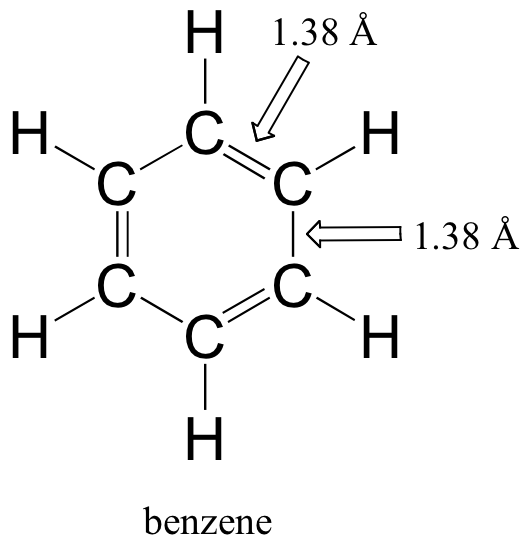
Molecular orbital theory is especially helpful in explaining the unique properties of a class of compounds called aromatics. Benzene, a common organic solvent, is the simplest example of an aromatic compound. Although benzene is most often drawn with three double bonds and three single bonds (Figure \(\PageIndex{4}\)), it is known that all of the carbon-carbon bonds in benzene are exactly the same length - 1.38 Å. This is shorter than a typical carbon-carbon single bond (about 1.54 Å), and slightly longer than a typical carbon-carbon double bond (about 1.34 Å).

Figure \(\PageIndex{4}\): (left( Simplified and incorrect three-doube bond/three single bond picture of bonding benzene. (right) The (2p_z\) atomic orbitals of the carbons overlap strongly above and below the ring.

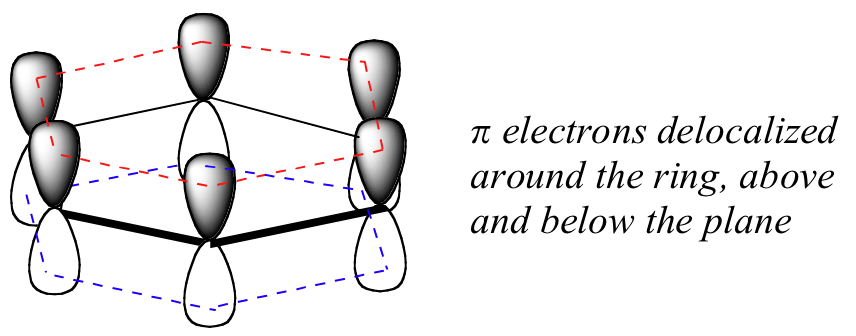
Benzene is also a cyclic molecule in which all of the ring atoms are sp²-hybridized that allows the π electrons to be delocalized in molecular orbitals that extend all the way around the ring, above and below the plane of the ring. For this to happen, of course, the ring must be planar – otherwise the 2p_z orbitals could not overlap properly. Benzene was experimentally confirmed to be flat molecule by Dame Kathleen Londsale with X-ray crystallography.

As shown in Figure \(\PageIndex{5}\), the cyclic array of six \2P_z\)-orbitals (one on each carbon) overlap to generate six molecular orbitals, three bonding and three antibonding. The plus and minus signs shown in the diagram do not represent electrostatic charge, but refer to phase signs in the equations that describe these orbitals (in the diagram the phases are also color coded). When the phases correspond, the orbitals overlap to generate a common region of like phase, with those orbitals having the greatest overlap (e.g. π₁) being lowest in energy. The remaining carbon valence electrons then occupy these molecular orbitals in pairs, resulting in a fully occupied (6 electrons) set of bonding molecular orbitals.

Figure \(\PageIndex{5}\): The Molecular Orbitals of Benzene.

Aromaticity

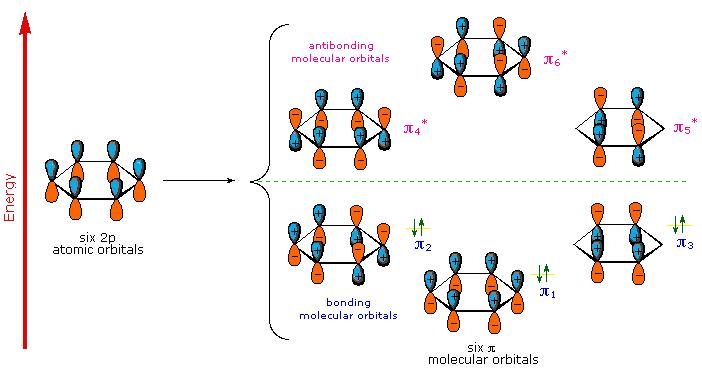
It is this completely filled set of bonding orbitals, or closed shell, that gives the benzene ring its thermodynamic and chemical stability, just as a filled valence shell octet confers stability on the inert gases. This added stability is call aromaticity. and is discuss in more detail in organic chemistry courses.

Molecular Orbitals and Resonance Structures

Resonance structures can be used to describe the bonding in molecules such as ozone (O₃) and the nitrite ion (NO₂⁻). We showed that ozone can be represented by either of these Lewis electron structures:

Although the VSEPR model correctly predicts that both species are bent, it gives no information about their bond orders.

Experimental evidence indicates that ozone has a bond angle of 117.5°. Because this angle is close to 120°, it is likely that the central oxygen atom in ozone is trigonal planar and sp² hybridized. If we assume that the terminal oxygen atoms are also sp² hybridized, then we obtain the \(\sigma\)-bonded framework shown in Figure \(\PageIndex{6}\). Two of the three sp² lobes on the central O are used to form O–O sigma bonds, and the third has a lone pair of electrons. Each terminal oxygen atom has two lone pairs of electrons that are also in sp² lobes. In addition, each oxygen atom has one unhybridized 2p orbital perpendicular to the molecular plane. The \(\sigma\) bonds and lone pairs account for a total of 14 electrons (five lone pairs and two \(\sigma\) bonds, each containing 2 electrons). Each oxygen atom in ozone has 6 valence electrons, so O₃ has a total of 18 valence electrons. Subtracting 14 electrons from the total gives us 4 electrons that must occupy the three unhybridized 2p orbitals.

Figure \(\PageIndex{6}\): Bonding in Ozone. (a) In the formation of the \(\sigma\)-bonded framework, three sets of oxygen sp² hybrid orbitals overlap to give two O–O \(\sigma\) bonds and five lone pairs, two on each terminal O and one on the central O. The \(\sigma\) bonds and lone pairs account for 14 of the 18 valence electrons of O₃. (b) One unhybridized 2p_z orbital remains on each oxygen atom that is available for \(\pi\) bonding. The unhybridized 2p_z orbital on each terminal O atom has a single electron, whereas the unhybridized 2p_z orbital on the central O atom has 2 electrons.

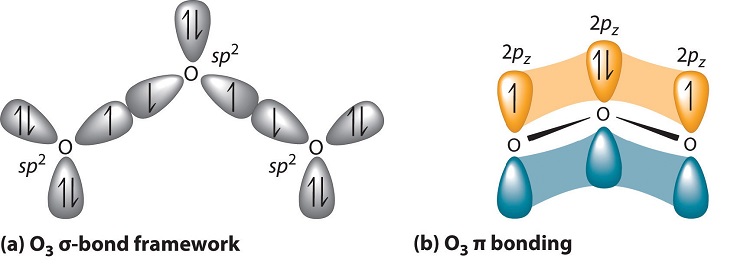
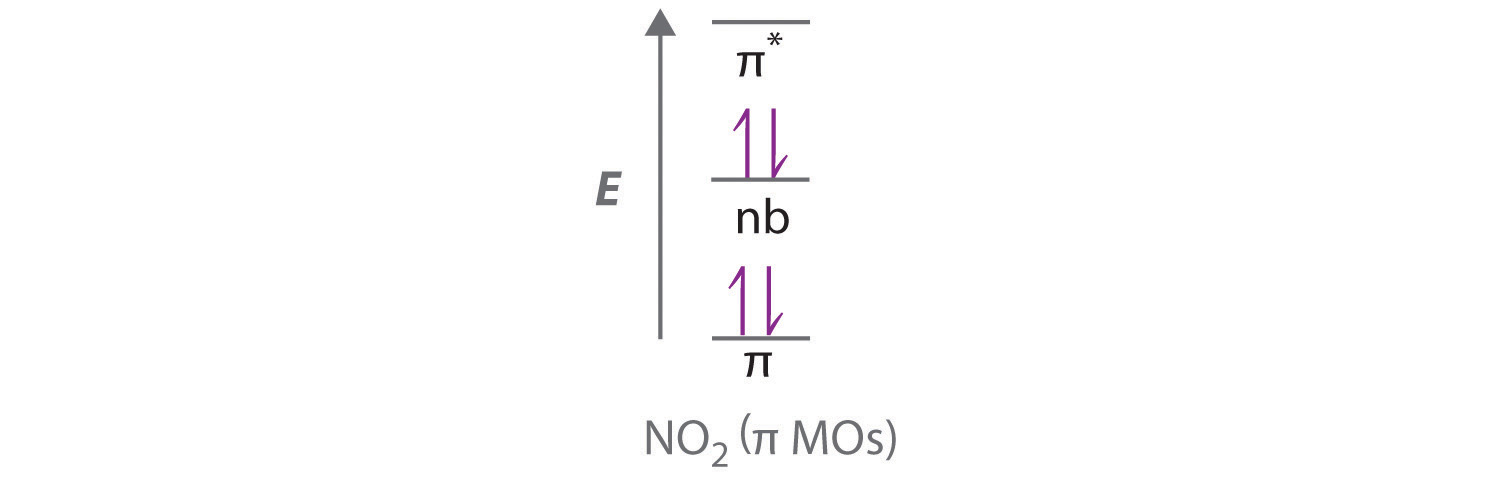
With a molecular orbital approach to describe the \(\pi\) bonding, three 2p atomic orbitals give us three molecular orbitals, as shown in Figure \(\PageIndex{7}\). One of the molecular orbitals is a \(\pi\) bonding molecular orbital, which is shown as a banana-shaped region of electron density above and below the molecular plane. This region has no nodes perpendicular to the O₃ plane. The molecular orbital with the highest energy has two nodes that bisect the O–O \(\sigma\) bonds; it is a \(\pi\)* antibonding orbital. The third molecular orbital contains a single node that is perpendicular to the O₃ plane and passes through the central O atom; it is a nonbonding molecular orbital. Because electrons in nonbonding orbitals are neither bonding nor antibonding, they are ignored in calculating bond orders.

Figure \(\PageIndex{7}\): \(\pi\) Bonding in Ozone. The three unhybridized 2pz atomic orbitals interact with one another to form three molecular orbitals: one \(\pi\) bonding orbital at lower energy, one \(\pi\)* antibonding orbital at higher energy, and a nonbonding orbital in between. Placing four electrons in this diagram fills the bonding and nonbonding orbitals. With one filled \(\pi\) bonding orbital holding three atoms together, the net \(\pi\) bond order is \(½\) per O–O bond. The combined \(\sigma/\pi\) bond order is thus \(1 \;½\)) for each O–O bond.

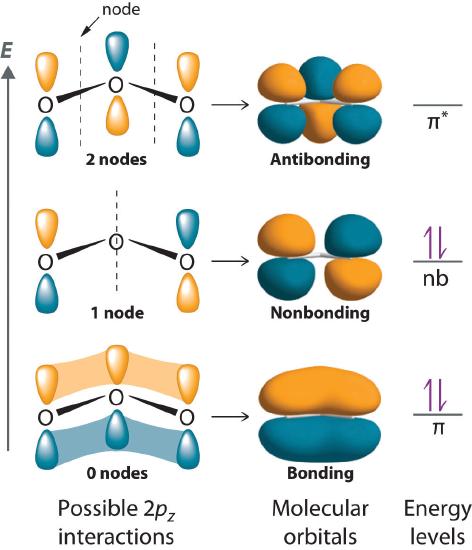
We can now place the remaining four electrons in the three energy levels shown in Figure \(\PageIndex{7}\), thereby filling the \(\pi\) bonding and the nonbonding levels. The result is a single \(\pi\) bond holding three oxygen atoms together, or \(½ \pi\) bond per O–O. We therefore predict the overall O–O bond order to be \(½ \pi\) bond plus 1 \(\sigma\) bond), just as predicted using resonance structures. The molecular orbital approach, however, shows that the \(\pi\) nonbonding orbital is localized on the terminal O atoms, which suggests that they are more electron rich than the central O atom. The reactivity of ozone is consistent with the predicted charge localization.

Resonance structures are a crude way of describing molecular orbitals that extend over more than two atoms.

Example \(\PageIndex{1}\)

Describe the bonding in the nitrite ion in terms of a combination of hybrid atomic orbitals and molecular orbitals. Lewis dot structures and the VSEPR model predict that the NO₂⁻ ion is bent.

Given: chemical species and molecular geometry

Asked for: bonding description using hybrid atomic orbitals and molecular orbitals

Strategy:

1. Calculate the number of valence electrons in NO₂⁻. From the structure, predict the type of atomic orbital hybridization in the ion.
2. Predict the number and type of molecular orbitals that form during bonding. Use valence electrons to fill these orbitals and then calculate the number of electrons that remain.
3. If there are unhybridized orbitals, place the remaining electrons in these orbitals in order of increasing energy. Calculate the bond order and describe the bonding.

Solution:

A The lone pair of electrons on nitrogen and a bent structure suggest that the bonding in NO₂⁻ is similar to the bonding in ozone. This conclusion is supported by the fact that nitrite also contains 18 valence electrons (5 from N and 6 from each O, plus 1 for the −1 charge). The bent structure implies that the nitrogen is sp² hybridized.

B If we assume that the oxygen atoms are sp² hybridized as well, then we can use two sp² hybrid orbitals on each oxygen and one sp² hybrid orbital on nitrogen to accommodate the five lone pairs of electrons. Two sp² hybrid orbitals on nitrogen form \(\sigma\) bonds with the remaining sp² hybrid orbital on each oxygen. The \(\sigma\) bonds and lone pairs account for 14 electrons. We are left with three unhybridized 2p orbitals, one on each atom, perpendicular to the plane of the molecule, and 4 electrons. Just as with ozone, these three 2p orbitals interact to form bonding, nonbonding, and antibonding \(\pi\) molecular orbitals. The bonding molecular orbital is spread over the nitrogen and both oxygen atoms.

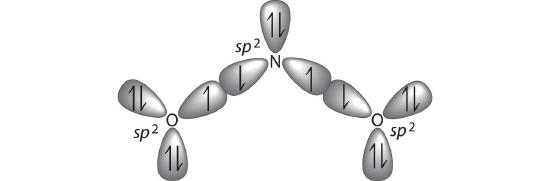
C Placing 4 electrons in the energy-level diagram fills both the bonding and nonbonding molecular orbitals and gives a \(\pi\) bond order of 1/2 per N–O bond. The overall N–O bond order is \(1\;\frac{1}{2}\), consistent with a resonance structure.

Exercise \(\PageIndex{1}\)

Describe the bonding in the formate ion (HCO₂⁻), in terms of a combination of hybrid atomic orbitals and molecular orbitals.

Answer

Like nitrite, formate is a planar polyatomic ion with 18 valence electrons. The \(\sigma\) bonding framework can be described in terms of sp² hybridized carbon and oxygen, which account for 14 electrons. The three unhybridized 2p orbitals (on C and both O atoms) form three \(\pi\) molecular orbitals, and the remaining 4 electrons occupy both the bonding and nonbonding \(\pi\) molecular orbitals. The overall C–O bond order is therefore \(frac{3}{2}\)

The Chemistry of Vision

Hydrocarbons in which two or more carbon–carbon double bonds are directly linked by carbon–carbon single bonds are generally more stable than expected because of resonance. Because the double bonds are close enough to interact electronically with one another, the \(\pi\) electrons are shared over all the carbon atoms, as illustrated for 1,3-butadiene in Figure \(\PageIndex{8}\). As the number of interacting atomic orbitals increases, the number of molecular orbitals increases, the energy spacing between molecular orbitals decreases, and the systems become more stable (Figure \(\PageIndex{9}\)). Thus as a chain of alternating double and single bonds becomes longer, the energy required to excite an electron from the highest-energy occupied (bonding) orbital to the lowest-energy unoccupied (antibonding) orbital decreases. If the chain is long enough, the amount of energy required to excite an electron corresponds to the energy of visible light. For example, vitamin A is yellow because its chain of five alternating double bonds is able to absorb violet light. Many of the colors we associate with dyes result from this same phenomenon; most dyes are organic compounds with alternating double bonds.

Figure \(\PageIndex{8}\): \(\pi\) Bonding in 1,3-Butadiene. (a) If each carbon atom is assumed to be sp² hybridized, we can construct a \(\sigma\)-bonded framework that accounts for the C–H and C–C single bonds, leaving four singly occupied 2p_z orbitals, one on each carbon atom. (b) As in ozone, these orbitals can interact, in this case to form four molecular orbitals. The molecular orbital at lowest energy is a bonding orbital with 0 nodes, the one at highest energy is antibonding with 3 nodes, and the two in the middle have 1 node and 2 nodes and are somewhere between bonding or antibonding and nonbonding, respectively. The energy of the molecular orbital increases with the number of nodes. With four electrons, only the two bonding orbitals are filled, consistent with the presence of two \(\pi\) bonds.

As the number of atomic orbitals increases, the difference in energy between the resulting molecular orbital energy levels decreases, which allows light of lower energy to be absorbed. As a result, organic compounds with long chains of carbon atoms and alternating single and double bonds tend to become more deeply colored as the number of double bonds increases.

Figure \(\PageIndex{9}\) Molecular Orbital Energy-Level Diagrams for a Chain of n Like Orbitals That Interact (n ≤ 5).

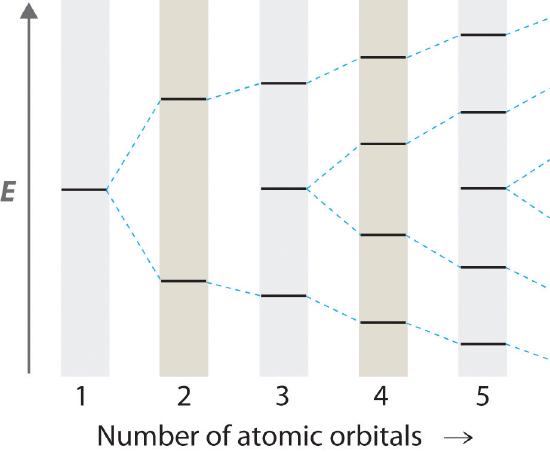
As the number of interacting atomic orbitals increases, the energy separation between the resulting molecular orbitals steadily decreases.

A derivative of vitamin A called retinal is used by the human eye to detect light and has a structure with alternating C=C double bonds. When visible light strikes retinal, the energy separation between the molecular orbitals is sufficiently close that the energy absorbed corresponds to the energy required to change one double bond in the molecule from cis, where like groups are on the same side of the double bond, to trans, where they are on opposite sides, initiating a process that causes a signal to be sent to the brain. If this mechanism is defective, we lose our vision in dim light. Once again, a molecular orbital approach to bonding explains a process that cannot be explained using any of the other approaches we have described.

Delocalization

Delocalization is central feature of molecular orbital theory where rather than the lone pair of electrons contained in localize bonds (as in the valence bond theory), electrons can exist in molecular orbitals that are spread over the entire molecule.

Summary

The \(\pi\) bonding between three or four atoms requires combining three or four unhybridized np orbitals on adjacent atoms to generate \(\pi\) bonding, antibonding, and nonbonding molecular orbitals extending over all of the atoms. Filling the resulting energy-level diagram with the appropriate number of electrons explains the bonding in molecules or ions that previously required the use of resonance structures in the Lewis electron-pair approach.

Contributors and Attributions

• Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)