15.2: The Equilibrium Constant
- Page ID
- 25168
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To know the relationship between the equilibrium constant and the rate constants for the forward and reverse reactions.
- To write an equilibrium constant expression for any reaction.
Because an equilibrium state is achieved when the forward reaction rate equals the reverse reaction rate, under a given set of conditions there must be a relationship between the composition of the system at equilibrium and the kinetics of a reaction (represented by rate constants). We can show this relationship using the decomposition reaction of \(\ce{N_2O_4}\) to \(\ce{NO2}\). Both the forward and reverse reactions for this system consist of a single elementary reaction, so the reaction rates are as follows:
\[\text{forward rate} = k_f[\ce{N2O4}] \nonumber \]
and
\[\text{reverse rate} = k_r[\ce{NO2}]^2\nonumber \]
At equilibrium, the forward rate equals the reverse rate (definition of equilibrium):
\[ k_f[\ce{N2O4}] = k_r[\ce{NO2}]^2 \label{Eq3} \]
so
\[\dfrac{k_f}{k_r}=\dfrac{[\ce{NO2}]^2}{[\ce{N2O4}]} \label{Eq4} \]
The ratio of the rate constants gives us a new constant, the equilibrium constant (\(K\)), which is defined as follows:
\[K=\dfrac{k_f}{k_r} \label{Eq5} \]
Hence there is a fundamental relationship between chemical kinetics and chemical equilibrium: under a given set of conditions, the composition of the equilibrium mixture is determined by the magnitudes of the rate constants for the forward and the reverse reactions.
The equilibrium constant is equal to the rate constant for the forward reaction divided by the rate constant for the reverse reaction.
A Video for Determining the Equilibrium Expression: Determining the Equilibrium Expression(opens in new window) [youtu.be]
Table \(\PageIndex{1}\) lists the initial and equilibrium concentrations from five different experiments using the reaction system described by Equation \(\ref{Eq3}\). At equilibrium the magnitude of the quantity \([\ce{NO2}]^2/[\ce{N2O4}]\) is essentially the same for all five experiments. In fact, no matter what the initial concentrations of \(\ce{NO2}\) and \(\ce{N2O4}\) are, at equilibrium the quantity \([\ce{NO2}]^2/[\ce{N2O4}]\) will always be \(6.53 \pm 0.03 \times 10^{-3}\) at 25°C, which corresponds to the ratio of the rate constants for the forward and reverse reactions. That is, at a given temperature, the equilibrium constant for a reaction always has the same value, even though the specific concentrations of the reactants and products vary depending on their initial concentrations.
| Initial Concentrations | Concentrations at Equilibrium | ||||
|---|---|---|---|---|---|
| Experiment | [\(\ce{N2O4}\)] (M) | [\(\ce{NO2}\)] (M) | [\(\ce{N2O4}\)] (M) | [\(\ce{NO2}\)] (M) | \(K = [\ce{NO2}]^2/[\ce{N2O4}]\) |
| 1 | 0.0500 | 0.0000 | 0.0417 | 0.0165 | \(6.54 \times 10^{-3}\) |
| 2 | 0.0000 | 0.1000 | 0.0417 | 0.0165 | \(6.54 \times 10^{-3}\) |
| 3 | 0.0750 | 0.0000 | 0.0647 | 0.0206 | \(6.56 \times 10^{-3}\) |
| 4 | 0.0000 | 0.0750 | 0.0304 | 0.0141 | \(6.54 \times 10^{-3}\) |
| 5 | 0.0250 | 0.0750 | 0.0532 | 0.0186 | \(6.50 \times 10^{-3}\) |
Developing an Equilibrium Constant Expression
In 1864, the Norwegian chemists Cato Guldberg (1836–1902) and Peter Waage (1833–1900) carefully measured the compositions of many reaction systems at equilibrium. They discovered that for any reversible reaction of the general form
\[aA+bB \rightleftharpoons cC+dD \label{Eq6} \]
where A and B are reactants, C and D are products, and a, b, c, and d are the stoichiometric coefficients in the balanced chemical equation for the reaction, the ratio of the product of the equilibrium concentrations of the products (raised to their coefficients in the balanced chemical equation) to the product of the equilibrium concentrations of the reactants (raised to their coefficients in the balanced chemical equation) is always a constant under a given set of conditions. This relationship is known as the law of mass action (or law of chemical equilibrium) and can be stated as follows:
\[K=\dfrac{[C]^c[D]^d}{[A]^a[B]^b} \label{Eq7} \]
where \(K\) is the equilibrium constant for the reaction. Equation \(\ref{Eq6}\) is called the equilibrium equation, and the right side of Equation \(\ref{Eq7}\) is called the equilibrium constant expression. The relationship shown in Equation \(\ref{Eq7}\) is true for any pair of opposing reactions regardless of the mechanism of the reaction or the number of steps in the mechanism.
The equilibrium constant can vary over a wide range of values. The values of \(K\) shown in Table \(\PageIndex{2}\), for example, vary by 60 orders of magnitude. Because products are in the numerator of the equilibrium constant expression and reactants are in the denominator, values of K greater than \(10^3\) indicate a strong tendency for reactants to form products. In this case, chemists say that equilibrium lies to the right as written, favoring the formation of products. An example is the reaction between \(H_2\) and \(Cl_2\) to produce \(HCl\), which has an equilibrium constant of \(1.6 \times 10^{33}\) at 300 K. Because \(H_2\) is a good reductant and \(Cl_2\) is a good oxidant, the reaction proceeds essentially to completion. In contrast, values of \(K\) less than \(10^{-3}\) indicate that the ratio of products to reactants at equilibrium is very small. That is, reactants do not tend to form products readily, and the equilibrium lies to the left as written, favoring the formation of reactants.
| Reaction | Temperature (K) | Equilibrium Constant (K) |
|---|---|---|
| *Equilibrium constants vary with temperature. The K values shown are for systems at the indicated temperatures. | ||
| \(S_{(s)}+O_{2(g)} \rightleftharpoons SO_{2(g)}\) | 300 | \(4.4 \times 10^{53}\) |
| \(2H_{2(g)}+O_{2(g)} \rightleftharpoons 2H2O_{(g)}\) | 500 | \(2.4 \times 10^{47}\) |
| \(H_{2(g)}+Cl_{2(g)} \rightleftharpoons 2HCl_{(g)}\) | 300 | \(1.6 \times 10^{33}\) |
| \(H_{2(g)}+Br_{2(g)} \rightleftharpoons 2HBr_{(g)}\) | 300 | \(4.1 \times 10^{18}\) |
| \(2NO_{(g)}+O_{2(g)} \rightleftharpoons 2NO_{2(g)}\) | 300 | \(4.2 \times 10^{13}\) |
| \(3H_{2(g)}+N_{2(g)} \rightleftharpoons 2NH_{3(g)}\) | 300 | \(2.7 \times 10^{8}\) |
| \(H_{2(g)}+D_{2(g)} \rightleftharpoons 2HD_{(g)}\) | 100 | \(1.92\) |
| \(H_{2(g)}+I_{2(g)} \rightleftharpoons 2HI_{(g)}\) | 300 | \(2.9 \times 10^{-1}\) |
| \(I_{2(g)} \rightleftharpoons 2I_{(g)}\) | 800 | \(4.6 \times 10^{-7}\) |
| \(Br_{2(g)} \rightleftharpoons 2Br_{(g)}\) | 1000 | \(4.0 \times 10^{-7}\) |
| \(Cl_{2(g)} \rightleftharpoons 2Cl_{(g)}\) | 1000 | \(1.8 \times 10^{-9}\) |
| \(F_{2(g)} \rightleftharpoons 2F_{(g)}\) | 500 | \(7.4 \times 10^{-13}\) |
You will also notice in Table \(\PageIndex{2}\) that equilibrium constants have no units, even though Equation \(\ref{Eq7}\) suggests that the units of concentration might not always cancel because the exponents may vary. In fact, equilibrium constants are calculated using “effective concentrations,” or activities, of reactants and products, which are the ratios of the measured concentrations to a standard state of 1 M. As shown in Equation \(\ref{Eq8}\), the units of concentration cancel, which makes \(K\) unitless as well:
\[ \dfrac{[A]_{measured}}{[A]_{standard\; state}}=\dfrac{\cancel{M}}{\cancel{M}} = \dfrac{\cancel{\frac{mol}{L}}}{\cancel{\frac{mol}{L}}} \label{Eq8} \]
Because equilibrium constants are calculated using “effective concentrations” relative to a standard state of 1 M, values of K are unitless.
Many reactions have equilibrium constants between 1000 and 0.001 (\(10^3 \ge K \ge 10^{-3}\)), neither very large nor very small. At equilibrium, these systems tend to contain significant amounts of both products and reactants, indicating that there is not a strong tendency to form either products from reactants or reactants from products. An example of this type of system is the reaction of gaseous hydrogen and deuterium, a component of high-stability fiber-optic light sources used in ocean studies, to form \(\ce{HD}\):
\[\ce{H2(g) + D2(g) <=> 2HD(g)} \nonumber \]
The equilibrium constant expression for this reaction is
\[K= \dfrac{[HD]^2}{[H_2][D_2]} \nonumber \]
with \(K\) varying between 1.9 and 4 over a wide temperature range (100–1000 K). Thus an equilibrium mixture of \(H_2\), \(D_2\), and \(HD\) contains significant concentrations of both product and reactants.
Figure \(\PageIndex{3}\) summarizes the relationship between the magnitude of K and the relative concentrations of reactants and products at equilibrium for a general reaction, written as reactants \(\rightleftharpoons\) products. Because there is a direct relationship between the kinetics of a reaction and the equilibrium concentrations of products and reactants (Equations \(\ref{Eq8}\) and \(\ref{Eq7}\)), when \(k_f \gg k_r\), \(K\) is a large number, and the concentration of products at equilibrium predominate. This corresponds to an essentially irreversible reaction. Conversely, when \(k_f \ll k_r\), \(K\) is a very small number, and the reaction produces almost no products as written. Systems for which \(k_f ≈ k_r\) have significant concentrations of both reactants and products at equilibrium.
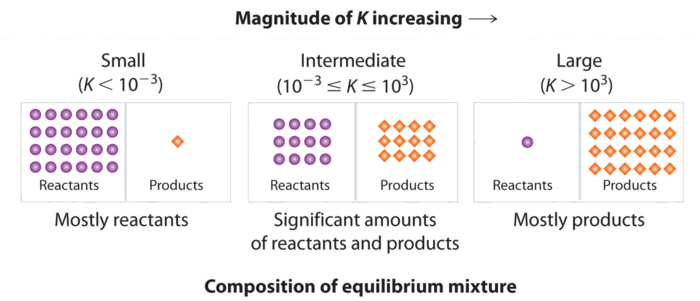
A large value of the equilibrium constant \(K\) means that products predominate at equilibrium; a small value means that reactants predominate at equilibrium.
Write the equilibrium constant expression for each reaction.
- \(\ce{N2(g) + 3H2(g) <=> 2NH3(g)}\)
- \(\ce{CO(g) + 1/2 O2(g) <=> CO2(g)}\)
- \(\ce{2CO2(g) <=> 2CO(g) + O2(g)}\)
Given: balanced chemical equations
Asked for: equilibrium constant expressions
Strategy:
Refer to Equation \(\ref{Eq7}\). Place the arithmetic product of the concentrations of the products (raised to their stoichiometric coefficients) in the numerator and the product of the concentrations of the reactants (raised to their stoichiometric coefficients) in the denominator.
Solution:
The only product is ammonia, which has a coefficient of 2. For the reactants, \(\ce{N2}\) has a coefficient of 1 and \(\ce{H2}\) has a coefficient of 3. The equilibrium constant expression is as follows:
\[\dfrac{[\ce{NH3}]^2}{[\ce{N2}][\ce{H2}]^3} \nonumber \]
The only product is carbon dioxide, which has a coefficient of 1. The reactants are \(\ce{CO}\), with a coefficient of 1, and \(\ce{O2}\), with a coefficient of \(\frac{1}{2}\). Thus the equilibrium constant expression is as follows:
\[\dfrac{[\ce{CO2}]}{[\ce{CO}][\ce{O2}]^{1/2}} \nonumber \]
This reaction is the reverse of the reaction in part b, with all coefficients multiplied by 2 to remove the fractional coefficient for \(\ce{O2}\). The equilibrium constant expression is therefore the inverse of the expression in part b, with all exponents multiplied by 2
\[\dfrac{[\ce{CO}]^2[\ce{O2}]}{[\ce{CO2}]^2} \nonumber \]
Write the equilibrium constant expression for each reaction.
- \(\ce{N2O(g) <=> N2(g) + 1/2O2(g)}\)
- \(\ce{2C8H18(g) + 25O2(g) <=> 16CO2(g) + 18H2O(g)}\)
- \(\ce{H2(g) + I2(g) <=> 2HI(g)}\)
- Answer a
-
\(K=\dfrac{[N_2][O_2]^{1/2}}{[N_2O]}\)
- Answer b
-
\(K=\dfrac{[CO_2]^{16}[H_2O]^{18}}{[C_8H_{18}]^2[O_2]^{25}}\)
- Answer c
-
\(K=\dfrac{[HI]^2}{[H_2][I_2]}\)
Predict which systems at equilibrium will (a) contain essentially only products, (b) contain essentially only reactants, and (c) contain appreciable amounts of both products and reactants.
- \(H_{2(g)}+I_{2(g)} \rightleftharpoons 2HI_{(g)}\;\;\; K_{(700K)}=54\)
- \(2CO_{2(g)} \rightleftharpoons 2CO_{(g)}+O_{2(g)}\;\;\; K_{(1200K)}=3.1 \times 10^{-18}\)
- \(PCl_{5(g)} \rightleftharpoons PCl_{3(g)}+Cl_{2(g)}\;\;\; K_{(613K)}=97\)
- \(2O_{3(g)} \rightleftharpoons 3O_{2(g)} \;\;\; K_{(298 K)}=5.9 \times 10^{55}\)
Given: systems and values of \(K\)
Asked for: composition of systems at equilibrium
Strategy:
Use the value of the equilibrium constant to determine whether the equilibrium mixture will contain essentially only products, essentially only reactants, or significant amounts of both.
Solution:
- Only system 4 has \(K \gg 10^3\), so at equilibrium it will consist of essentially only products.
- System 2 has \(K \ll 10^{-3}\), so the reactants have little tendency to form products under the conditions specified; thus, at equilibrium the system will contain essentially only reactants.
- Both systems 1 and 3 have equilibrium constants in the range \(10^3 \ge K \ge 10^{-3}\), indicating that the equilibrium mixtures will contain appreciable amounts of both products and reactants.
Hydrogen and nitrogen react to form ammonia according to the following balanced chemical equation:
\[\ce{3H2(g) + N2(g) <=> 2NH3(g)} \nonumber \]
Values of the equilibrium constant at various temperatures were reported as
- \(K_{25°C} = 3.3 \times 10^8\),
- \(K_{177°C} = 2.6 \times 10^3\), and
- \(K_{327°C} = 4.1\).
- At which temperature would you expect to find the highest proportion of \(H_2\) and \(N_2\) in the equilibrium mixture?
- Assuming that the reaction rates are fast enough so that equilibrium is reached quickly, at what temperature would you design a commercial reactor to operate to maximize the yield of ammonia?
- Answer a
-
327°C, where \(K\) is smallest
- Answer b
-
25°C
Video which Discusses What Does K Tell us About a Reaction?: What Does K Tell us About a Reaction?(opens in new window) [youtu.be]
Variations in the Form of the Equilibrium Constant Expression
Because equilibrium can be approached from either direction in a chemical reaction, the equilibrium constant expression and thus the magnitude of the equilibrium constant depend on the form in which the chemical reaction is written. For example, if we write the reaction described in Equation \(\ref{Eq6}\) in reverse, we obtain the following:
\[cC+dD \rightleftharpoons aA+bB \label{Eq10} \]
The corresponding equilibrium constant \(K′\) is as follows:
\[K'=\dfrac{[A]^a[B]^b}{[C]^c[D]^d} \label{Eq11} \]
This expression is the inverse of the expression for the original equilibrium constant, so \(K′ = 1/K\). That is, when we write a reaction in the reverse direction, the equilibrium constant expression is inverted. For instance, the equilibrium constant for the reaction \(\ce{N2O4 <=> 2NO2}\) is as follows:
\[K=\dfrac{[\ce{NO2}]^2}{[\ce{N2O4}]} \label{Eq12} \]
but for the opposite reaction, \(2 NO_2 \rightleftharpoons N_2O_4\), the equilibrium constant K′ is given by the inverse expression:
\[K'=\dfrac{[\ce{N2O4}]}{[\ce{NO2}]^2} \label{Eq13} \]
Consider another example, the formation of water:
\[\ce{2H2(g) + O2(g) <=> 2H2O(g)}. \nonumber \]
Because \(\ce{H2}\) is a good reductant and \(\ce{O2}\) is a good oxidant, this reaction has a very large equilibrium constant (\(K = 2.4 \times 10^{47}\) at 500 K). Consequently, the equilibrium constant for the reverse reaction, the decomposition of water to form \(\ce{O2}\) and \(\ce{H2}\), is very small: \(K′ = 1/K = 1/(2.4 \times 10^{47}) = 4.2 \times 10^{-48}\). As suggested by the very small equilibrium constant, and fortunately for life as we know it, a substantial amount of energy is indeed needed to dissociate water into \(\ce{H2}\) and \(\ce{O2}\).
The equilibrium constant for a reaction written in reverse is the inverse of the equilibrium constant for the reaction as written originally.
Writing an equation in different but chemically equivalent forms also causes both the equilibrium constant expression and the magnitude of the equilibrium constant to be different. For example, we could write the equation for the reaction
\[\ce{2NO2 <=> N2O4} \nonumber \]
as
\[\ce{NO2 <=> 1/2 N2O4} \nonumber \]
with the equilibrium constant K″ is as follows:
\[ K′′=\dfrac{[\ce{N2O4}]^{1/2}}{[\ce{NO2}]} \label{Eq14} \]
The values for K′ (Equation \(\ref{Eq13}\)) and K″ are related as follows:
\[ K′′=(K')^{1/2}=\sqrt{K'} \label{Eq15} \]
In general, if all the coefficients in a balanced chemical equation were subsequently multiplied by \(n\), then the new equilibrium constant is the original equilibrium constant raised to the \(n^{th}\) power.
A Video Discussing Relationships Involving Equilibrium Constants: Relationships Involving Equilibrium Constants(opens in new window) [youtu.be] (opens in new window)
At 745 K, K is 0.118 for the following reaction:
\[\ce{N2(g) + 3H2(g) <=> 2NH3(g)} \nonumber \]
What is the equilibrium constant for each related reaction at 745 K?
- \(\ce{2NH3(g) <=> N2(g) + 3H2(g)}\)
- \(\ce{1/2 N2(g) + 3/2 H2(g) <=> NH3(g)}\)
Given: balanced equilibrium equation, \(K\) at a given temperature, and equations of related reactions
Asked for: values of \(K\) for related reactions
Strategy:
Write the equilibrium constant expression for the given reaction and for each related reaction. From these expressions, calculate \(K\) for each reaction.
Solution:
The equilibrium constant expression for the given reaction of \(N_{2(g)}\) with \(H_{2(g)}\) to produce \(NH_{3(g)}\) at 745 K is as follows:
\[K=\dfrac{[NH_3]^2}{[N_2][H_2]^3}=0.118 \nonumber \]
This reaction is the reverse of the one given, so its equilibrium constant expression is as follows:
\[K'=\dfrac{1}{K}=\dfrac{[N_2][H_2]^3}{[NH_3]^2}=\dfrac{1}{0.118}=8.47 \nonumber \]
In this reaction, the stoichiometric coefficients of the given reaction are divided by 2, so the equilibrium constant is calculated as follows:
\[K′′=\dfrac{[NH_3]}{[N_2]^{1/2}[H_2]^{3/2}}=K^{1/2}=\sqrt{K}=\sqrt{0.118} = 0.344 \nonumber \]
At 527°C, the equilibrium constant for the reaction
\[\ce{2SO2(g) + O2(g) <=> 2SO3(g)} \nonumber \]
is \(7.9 \times 10^4\). Calculate the equilibrium constant for the following reaction at the same temperature:
\[\ce{SO3(g) <=> SO2(g) + 1/2 O2(g)} \nonumber \]
- Answer
-
\(3.6 \times 10^{-3}\)
Equilibrium Constant Expressions for Systems that Contain Gases
For reactions that involve species in solution, the concentrations used in equilibrium calculations are usually expressed in moles/liter. For gases, however, the concentrations are usually expressed in terms of partial pressures rather than molarity, where the standard state is 1 atm of pressure. The symbol \(K_p\) is used to denote equilibrium constants calculated from partial pressures. For the general reaction \(aA+bB \rightleftharpoons cC+dD\), in which all the components are gases, the equilibrium constant expression can be written as the ratio of the partial pressures of the products and reactants (each raised to its coefficient in the chemical equation):
\[K_p=\dfrac{(P_C)^c(P_D)^d}{(P_A)^a(P_B)^b} \label{Eq16} \]
Thus \(K_p\) for the decomposition of \(N_2O_4\) (Equation 15.1) is as follows:
\[K_p=\dfrac{(P_{NO_2})^2}{P_{N_2O_4}} \label{Eq17} \]
Like \(K\), \(K_p\) is a unitless quantity because the quantity that is actually used to calculate it is an “effective pressure,” the ratio of the measured pressure to a standard state of 1 bar (approximately 1 atm), which produces a unitless quantity. The “effective pressure” is called the fugacity, just as activity is the effective concentration.
Because partial pressures are usually expressed in atmospheres or mmHg, the molar concentration of a gas and its partial pressure do not have the same numerical value. Consequently, the numerical values of \(K\) and \(K_p\) are usually different. They are, however, related by the ideal gas constant (\(R\)) and the absolute temperature (\(T\)):
\[\color{red} K_p = K(RT)^{Δn} \label{Eq18} \]
where \(K\) is the equilibrium constant expressed in units of concentration and \(Δn\) is the difference between the numbers of moles of gaseous products and gaseous reactants (\(n_p − n_r\)). The temperature is expressed as the absolute temperature in Kelvin. According to Equation \(\ref{Eq18}\), \(K_p = K\) only if the moles of gaseous products and gaseous reactants are the same (i.e., \(Δn = 0\)). For the decomposition of \(N_2O_4\), there are 2 mol of gaseous product and 1 mol of gaseous reactant, so \(Δn = 1\). Thus, for this reaction,
\[K_p = K(RT)^1 = KRT \nonumber \]
The equilibrium constant for the reaction of nitrogen and hydrogen to give ammonia is 0.118 at 745 K. The balanced equilibrium equation is as follows:
\[\ce{N2(g) + 3H2(g) <=> 2NH3(g)} \nonumber \]
What is \(K_p\) for this reaction at the same temperature?
Given: equilibrium equation, equilibrium constant, and temperature
Asked for: \(K_p\)
Strategy:
Use the coefficients in the balanced chemical equation to calculate \(Δn\). Then use Equation \(\ref{Eq18}\) to calculate \(K\) from \(K_p\).
Solution:
This reaction has 2 mol of gaseous product and 4 mol of gaseous reactants, so \(\Delta{n} = (2 − 4) = −2\). We know \(K\), and \(T = 745\; K\). Thus, from Equation \(\ref{Eq15}\), we have the following:
\[ \begin{align*} K_p &=K(RT)^{-2} \\[4pt] &=\dfrac{K}{(RT)^2} \\[4pt] &=\dfrac{0.118}{\{ [0.08206(L \cdot atm)/(mol \cdot K)][745\; K]\}^2} \\[4pt] &=3.16 \times 10^{-5} \end{align*} \nonumber \]
Because \(K_p\) is a unitless quantity, the answer is \( K_p = 3.16 \times 10^{-5}\).
Calculate \(K_p\) for the reaction
\[\ce{2SO2(g) + O2(g) \rightleftharpoons 2SO3(g)} \nonumber \]
at 527°C, if \(K = 7.9 \times 10^4\) at this temperature.
- Answer
-
\(K_p = 1.2 \times 10^3\)
Video Discussing Converting Kc to Kp: Converting Kc to Kp(opens in new window) [youtu.be]
Equilibrium Constant Expressions for the Sums of Reactions
Chemists frequently need to know the equilibrium constant for a reaction that has not been previously studied. In such cases, the desired reaction can often be written as the sum of other reactions for which the equilibrium constants are known. The equilibrium constant for the unknown reaction can then be calculated from the tabulated values for the other reactions.
To illustrate this procedure, let’s consider the reaction of \(\ce{N2}\) with \(\ce{O2}\) to give \(\ce{NO2}\). This reaction is an important source of the \(\ce{NO2}\) that gives urban smog its typical brown color. The reaction normally occurs in two distinct steps. In the first reaction (step 1), \(\ce{N2}\) reacts with \(\ce{O2}\) at the high temperatures inside an internal combustion engine to give \(\ce{NO}\). The released \(\ce{NO}\) then reacts with additional \(\ce{O2}\) to give \(\ce{NO2}\) (step 2). The equilibrium constant for each reaction at 100°C is also given.
\(\ce{N2(g) + O2(g) <=> 2NO(g)}\;\; K_1=2.0 \times 10^{-25} \label{step 1}\)
\(\ce{2NO(g) + O2(g) <=> 2NO2(g)}\;\;\;K_2=6.4 \times 10^9 \label{step 2}\)
Summing reactions (step 1) and (step 2) gives the overall reaction of \(N_2\) with \(O_2\):
\(\ce{N2(g) + 2O2(g) <=> 2NO2(g)} \;\;\;K_3=? \label{overall reaction 3}\)
The equilibrium constant expressions for the reactions are as follows:
\[K_1=\dfrac{[NO]^2}{[N_2][O_2]}\;\;\; K_2=\dfrac{[NO_2]^2}{[NO]^2[O_2]}\;\;\; K_3=\dfrac{[NO_2]^2}{[N_2][O_2]^2} \nonumber \]
What is the relationship between \(K_1\), \(K_2\), and \(K_3\), all at 100°C? The expression for \(K_1\) has \([NO]^2\) in the numerator, the expression for \(K_2\) has \([NO]^2\) in the denominator, and \([NO]^2\) does not appear in the expression for \(K_3\). Multiplying \(K_1\) by \(K_2\) and canceling the \([NO]^2\) terms,
\[ K_1K_2=\dfrac{\cancel{[NO]^2}}{[N_2][O_2]} \times \dfrac{[NO_2]^2}{\cancel{[NO]^2}[O_2]}=\dfrac{[NO_2]^2}{[N_2][O_2]^2}=K_3 \nonumber \]
Thus the product of the equilibrium constant expressions for \(K_1\) and \(K_2\) is the same as the equilibrium constant expression for \(K_3\):
\[K_3 = K_1K_2 = (2.0 \times 10^{-25})(6.4 \times 10^9) = 1.3 \times 10^{-15} \nonumber \]
The equilibrium constant for a reaction that is the sum of two or more reactions is equal to the product of the equilibrium constants for the individual reactions. In contrast, recall that according to Hess’s Law, \(ΔH\) for the sum of two or more reactions is the sum of the ΔH values for the individual reactions.
To determine \(K\) for a reaction that is the sum of two or more reactions, add the reactions but multiply the equilibrium constants.
The following reactions occur at 1200°C:
- \(CO_{(g)}+3H_{2(g)} \rightleftharpoons CH_{4(g)}+H_2O_{(g)} \;\;\;K_1=9.17 \times 10^{-2}\)
- \(CH_{4(g)}+2H_2S_{(g)} \rightleftharpoons CS_{2(g)}+4H_{2(g})\;\;\; K_2=3.3 \times 10^4\)
Calculate the equilibrium constant for the following reaction at the same temperature.
- \(CO_{(g)}+2H_2S_{(g)} \rightleftharpoons CS_{2(g)}+H_2O_{(g)}+H_{2(g)}\;\;\; K_3=?\)
Given: two balanced equilibrium equations, values of \(K\), and an equilibrium equation for the overall reaction
Asked for: equilibrium constant for the overall reaction
Strategy:
Arrange the equations so that their sum produces the overall equation. If an equation had to be reversed, invert the value of \(K\) for that equation. Calculate \(K\) for the overall equation by multiplying the equilibrium constants for the individual equations.
Solution:
The key to solving this problem is to recognize that reaction 3 is the sum of reactions 1 and 2:
\[CO_{(g)}+ \cancel{3H_{2(g)}} \rightleftharpoons \cancel{CH_{4(g)}} + H_2O_{(g)} \nonumber \]
\[\cancel{CH_{4(g)}} +2H_2S_{(g)} \rightleftharpoons CS_{2(g)} + \cancel{3H_{2(g)}} + H_{2(g)} \nonumber \]
\[ CO_{(g)} + 3H_{2(g)} \rightleftharpoons CS_{2(g)}+H_2O_{(g)}+H_{2(g)} \nonumber \]
The values for \(K_1\) and \(K_2\) are given, so it is straightforward to calculate \(K_3\):
\[K_3 = K_1K_2 = (9.17 \times 10^{-2})(3.3 \times 10^4) = 3.03 \times 10^3 \nonumber \]
In the first of two steps in the industrial synthesis of sulfuric acid, elemental sulfur reacts with oxygen to produce sulfur dioxide. In the second step, sulfur dioxide reacts with additional oxygen to form sulfur trioxide. The reaction for each step is shown, as is the value of the corresponding equilibrium constant at 25°C. Calculate the equilibrium constant for the overall reaction at this same temperature.
- \(\frac{1}{8}S_{8(s)}+O_{2(g)} \rightleftharpoons SO_{2(g)}\;\;\; K_1=4.4 \times 10^{53}\)
- \(SO_{2(g)}+\frac{1}{2}O_{2(g)} \rightleftharpoons SO_{3(g)}\;\;\; K_2=2.6 \times 10^{12}\)
- \(\frac{1}{8}S_{8(s)}+\frac{3}{2}O_{2(g)} \rightleftharpoons SO_{3(g)}\;\;\; K_3=?\)
- Answer
-
\(K_3 = 1.1 \times 10^{66}\)
Summary
The ratio of the rate constants for the forward and reverse reactions at equilibrium is the equilibrium constant (\(K\)), a unitless quantity. The composition of the equilibrium mixture is therefore determined by the magnitudes of the forward and reverse rate constants at equilibrium. Under a given set of conditions, a reaction will always have the same \(K\). For a system at equilibrium, the law of mass action relates \(K\) to the ratio of the equilibrium concentrations of the products to the concentrations of the reactants raised to their respective powers to match the coefficients in the equilibrium equation. The ratio is called the equilibrium constant expression. When a reaction is written in the reverse direction, \(K\) and the equilibrium constant expression are inverted. For gases, the equilibrium constant expression can be written as the ratio of the partial pressures of the products to the partial pressures of the reactants, each raised to a power matching its coefficient in the chemical equation. An equilibrium constant calculated from partial pressures (\(K_p\)) is related to \(K\) by the ideal gas constant (\(R\)), the temperature (\(T\)), and the change in the number of moles of gas during the reaction. An equilibrium system that contains products and reactants in a single phase is a homogeneous equilibrium; a system whose reactants, products, or both are in more than one phase is a heterogeneous equilibrium. When a reaction can be expressed as the sum of two or more reactions, its equilibrium constant is equal to the product of the equilibrium constants for the individual reactions.
- The law of mass action describes a system at equilibrium in terms of the concentrations of the products and the reactants.
- For a system involving one or more gases, either the molar concentrations of the gases or their partial pressures can be used.
- Definition of equilibrium constant in terms of forward and reverse rate constants: \[K=\dfrac{k_f}{k_r} \nonumber \]
- Equilibrium constant expression (law of mass action): \[K=\dfrac{[C]^c[D]^d}{[A]^a[B]^b} \nonumber \]
- Equilibrium constant expression for reactions involving gases using partial pressures: \[K_p=\dfrac{(P_C)^c(P_D)^d}{(P_A)^a(P_B)^b} \nonumber \]
- Relationship between \(K_p\) and \(K\): \[K_p = K(RT)^{Δn} \nonumber \]

