13.2: Electronegativity
- Page ID
- 15099
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Electronegativity is a measure of the tendency of an atom to attract a bonding pair of electrons. The Pauling scale is the most commonly used. Fluorine (the most electronegative element) is assigned a value of 4.0, and values range down to cesium and francium which are the least electronegative at 0.7.
What if two atoms of equal electronegativity bond together?
Consider a bond between two atoms, A and B. If the atoms are equally electronegative, both have the same tendency to attract the bonding pair of electrons, and so it will be found on average half way between the two atoms:
To get a bond like this, A and B would usually have to be the same atom. You will find this sort of bond in, for example, H2 or Cl2 molecules. Note: It's important to realize that this is an average picture. The electrons are actually in a molecular orbital, and are moving around all the time within that orbital. This sort of bond could be thought of as being a "pure" covalent bond - where the electrons are shared evenly between the two atoms.
What if B is slightly more electronegative than A?
B will attract the electron pair rather more than A does.
That means that the B end of the bond has more than its fair share of electron density and so becomes slightly negative. At the same time, the A end (rather short of electrons) becomes slightly positive. In the diagram, "\(\delta\)" (read as "delta") means "slightly" - so \(\delta+\) means "slightly positive".
A polar bond is a covalent bond in which there is a separation of charge between one end and the other - in other words in which one end is slightly positive and the other slightly negative. Examples include most covalent bonds. The hydrogen-chlorine bond in HCl or the hydrogen-oxygen bonds in water are typical.
If B is a lot more electronegative than A, then the electron pair is dragged right over to B's end of the bond. To all intents and purposes, A has lost control of its electron, and B has complete control over both electrons. Ions have been formed. The bond is then an ionic bond rather than a covalent bond.
A "spectrum" of bonds
The implication of all this is that there is no clear-cut division between covalent and ionic bonds. In a pure covalent bond, the electrons are held on average exactly half way between the atoms. In a polar bond, the electrons have been dragged slightly towards one end. How far does this dragging have to go before the bond counts as ionic? There is no real answer to that. Sodium chloride is typically considered an ionic solid, but even here the sodium has not completely lost control of its electron. Because of the properties of sodium chloride, however, we tend to count it as if it were purely ionic. Lithium iodide, on the other hand, would be described as being "ionic with some covalent character". In this case, the pair of electrons has not moved entirely over to the iodine end of the bond. Lithium iodide, for example, dissolves in organic solvents like ethanol - not something which ionic substances normally do.
- No electronegativity difference between two atoms leads to a pure non-polar covalent bond.
- A small electronegativity difference leads to a polar covalent bond.
- A large electronegativity difference leads to an ionic bond.
In a simple diatomic molecule like HCl, if the bond is polar, then the whole molecule is polar. What about more complicated molecules?
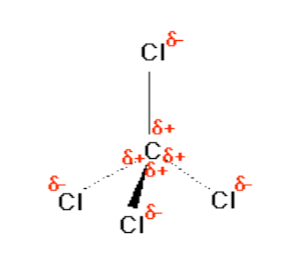

Consider CCl4, (left panel in figure above), which as a molecule is not polar - in the sense that it doesn't have an end (or a side) which is slightly negative and one which is slightly positive. The whole of the outside of the molecule is somewhat negative, but there is no overall separation of charge from top to bottom, or from left to right.
In contrast, CHCl3 is a polar molecule (right panel in figure above). The hydrogen at the top of the molecule is less electronegative than carbon and so is slightly positive. This means that the molecule now has a slightly positive "top" and a slightly negative "bottom", and so is overall a polar molecule.
A polar molecule will need to be "lop-sided" in some way.
Patterns of electronegativity in the Periodic Table
The distance of the electrons from the nucleus remains relatively constant in a periodic table row, but not in a periodic table column. The force between two charges is given by Coulomb’s law.
\[ F=k\dfrac{Q_1Q_2}{r^2} \]
In this expression, Q represents a charge, k represents a constant and r is the distance between the charges. When r = 2, then r2= 4. When r = 3, then r2 = 9. When r = 4, then r2 = 16. It is readily seen from these numbers that, as the distance between the charges increases, the force decreases very rapidly. This is called a quadratic change.
The result of this change is that electronegativity increases from bottom to top in a column in the periodic table even though there are more protons in the elements at the bottom of the column. Elements at the top of a column have greater electronegativities than elements at the bottom of a given column.
The overall trend for electronegativity in the periodic table is diagonal from the lower left corner to the upper right corner. Since the electronegativity of some of the important elements cannot be determined by these trends (they lie in the wrong diagonal), we have to memorize the following order of electronegativity for some of these common elements.
F > O > Cl > N > Br > I > S > C > H > metals
The most electronegative element is fluorine. If you remember that fact, everything becomes easy, because electronegativity must always increase towards fluorine in the Periodic Table.
This simplification ignores the noble gases. Historically this is because they were believed not to form bonds - and if they do not form bonds, they cannot have an electronegativity value. Even now that we know that some of them do form bonds, data sources still do not quote electronegativity values for them.
Trends in electronegativity across a period
The positively charged protons in the nucleus attract the negatively charged electrons. As the number of protons in the nucleus increases, the electronegativity or attraction will increase. Therefore electronegativity increases from left to right in a row in the periodic table. This effect only holds true for a row in the periodic table because the attraction between charges falls off rapidly with distance. The chart shows electronegativities from sodium to chlorine (ignoring argon since it does not does not form bonds).
Trends in electronegativity down a group
As you go down a group, electronegativity decreases. (If it increases up to fluorine, it must decrease as you go down.) The chart shows the patterns of electronegativity in Groups 1 and 7.
Explaining the patterns in electronegativity
The attraction that a bonding pair of electrons feels for a particular nucleus depends on:
- the number of protons in the nucleus;
- the distance from the nucleus;
- the amount of screening by inner electrons.
Why does electronegativity increase across a period?
Consider sodium at the beginning of period 3 and chlorine at the end (ignoring the noble gas, argon). Think of sodium chloride as if it were covalently bonded.
Both sodium and chlorine have their bonding electrons in the 3-level. The electron pair is screened from both nuclei by the 1s, 2s and 2p electrons, but the chlorine nucleus has 6 more protons in it. It is no wonder the electron pair gets dragged so far towards the chlorine that ions are formed. Electronegativity increases across a period because the number of charges on the nucleus increases. That attracts the bonding pair of electrons more strongly.
Why does electronegativity fall as you go down a group?
As you go down a group, electronegativity decreases because the bonding pair of electrons is increasingly distant from the attraction of the nucleus. Consider the hydrogen fluoride and hydrogen chloride molecules:
The bonding pair is shielded from the fluorine's nucleus only by the 1s2 electrons. In the chlorine case it is shielded by all the 1s22s22p6 electrons. In each case there is a net pull from the center of the fluorine or chlorine of +7. But fluorine has the bonding pair in the 2-level rather than the 3-level as it is in chlorine. If it is closer to the nucleus, the attraction is greater.
Diagonal relationships in the Periodic Table
At the beginning of periods 2 and 3 of the Periodic Table, there are several cases where an element at the top of one group has some similarities with an element in the next group. Three examples are shown in the diagram below. Notice that the similarities occur in elements which are diagonal to each other - not side-by-side.
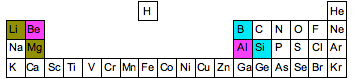
For example, boron is a non-metal with some properties rather like silicon. Unlike the rest of Group 2, beryllium has some properties resembling aluminum. And lithium has some properties which differ from the other elements in Group 1, and in some ways resembles magnesium. There is said to be a diagonal relationship between these elements. There are several reasons for this, but each depends on the way atomic properties like electronegativity vary around the Periodic Table. So we will have a quick look at this with regard to electronegativity - which is probably the simplest to explain.
Explaining the diagonal relationship with regard to electronegativity
Electronegativity increases across the Periodic Table. So, for example, the electronegativities of beryllium and boron are:
| Be | 1.5 |
| B | 2.0 |
Electronegativity falls as you go down the Periodic Table. So, for example, the electronegativities of boron and aluminum are:
| B | 2.0 |
| Al | 1.5 |
So, comparing Be and Al, you find the values are (by chance) exactly the same. The increase from Group 2 to Group 3 is offset by the fall as you go down Group 3 from boron to aluminum. Something similar happens from lithium (1.0) to magnesium (1.2), and from boron (2.0) to silicon (1.8). In these cases, the electronegativities are not exactly the same, but are very close.
Similar electronegativities between the members of these diagonal pairs means that they are likely to form similar types of bonds, and that will affect their chemistry. You may well come across examples of this later on in your course.

