12.E: Solids (Exercises)
- Page ID
- 6411
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)These are homework exercises to accompany the Textmap created for "Chemistry: Principles, Patterns, and Applications" by Bruce A. Averill and Patricia Eldredge. Complementary General Chemistry question banks can be found for other Textmaps and can be accessed here. In addition to these publicly available questions, access to private problems bank for use in exams and homework is available to faculty only on an individual basis; please contact Delmar Larsen for an account with access permission.
Application Problems
Problems marked with a ♦ involve multiple concepts.
1. ♦ Cadmium selenide (CdSe) is a semiconductor used in photoconductors and photoelectric cells that conduct electricity when illuminated. In a related process, a CdSe crystal can absorb enough energy to excite electrons from the valence band to the conduction band, and the excited electrons can return to the valence band by emitting light. The relative intensity and peak wavelength of the emitted light in one experiment are shown in the following table:
| Relative Intensity (%) | Wavelength (nm) | Temperature (°C) |
|---|---|---|
| 100 | 720 | 23 |
| 50 | 725 | 45 |
| 10 | 730 | 75 |
a. Explain why the emitted light shifts to longer wavelength at higher temperatures. (Hint: consider the expansion of the crystal and the resulting changes in orbital interactions when heated.)
b. Why does the relative intensity of the emitted light decrease as the temperature increases?
2. A large fraction of electrical energy is currently lost as heat during transmission due to the electrical resistance of transmission wires. How could superconducting technology improve the transmission of electrical power? What are some potential drawbacks of this technology?
3. Light-emitting diodes (LEDs) are semiconductor-based devices that are used in consumer electronics products ranging from digital clocks to fiber-optic telephone transmission lines. The color of the emitted light is determined in part by the band gap of the semiconductor. Electrons can be promoted to the conduction band and return to the valence band by emitting light or by increasing the magnitude of atomic vibrations in the crystal, which increases its temperature. If you wanted to increase the efficiency of an LED display, and thereby the intensity of the emitted light, would you increase or decrease the operating temperature of the LED? Explain your answer.
4. ♦ Strips of pure Au and Al are often used in close proximity to each other on circuit boards. As the boards become warm during use, however, the metals can diffuse, forming a purple alloy known as “the purple plague” between the strips. Because the alloy is electrically conductive, the board short-circuits. A structural analysis of the purple alloy showed that its structure contained a face-centered cubic (fcc) lattice of atoms of one element, with atoms of the other element occupying tetrahedral holes. What type of alloy is this? Which element is most likely to form the fcc lattice? Which element is most likely to occupy the tetrahedral holes? Explain your answers. What is the empirical formula of the “purple plague”?
5. ♦ Glasses are mixtures of oxides, the main component of which is silica (SiO2). Silica is called the glass former, while additives are referred to as glass modifiers. The crystalline lattice of the glass former breaks down during heating, producing the random atomic arrangements typical of a liquid. Adding a modifier and cooling the melt rapidly produces a glass. How does the three-dimensional structure of the glass differ from that of the crystalline glass former? Would you expect the melting point of a glass to be higher or lower than that of pure SiO2? Lead glass, a particular favorite of the Romans, was formed by adding lead oxide as the modifier. Would you expect lead glass to be more or less dense than soda-lime glass formed by adding sodium and potassium salts as modifiers?
6. Many glasses eventually crystallize, rendering them brittle and opaque. Modifying agents such as TiO2 are frequently added to molten glass to reduce their tendency to crystallize. Why does the addition of small amounts of TiO2 stabilize the amorphous structure of glass?
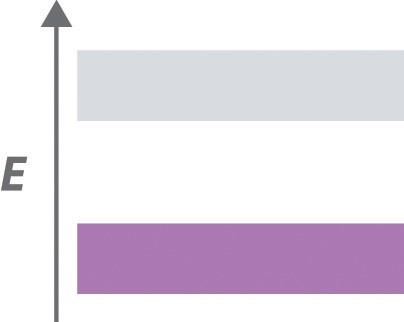
7. ♦ The carbon–carbon bond distances in polyacetylene (–CH=CH–)n alternate between short and long, resulting in the following band structure:
a. Is polyacetylene a metal, a semiconductor, or an insulator?
b. Based on its band structure, how would treating polyacetylene with a potent oxidant affect its electrical conductivity? What would be the effect of treating polyacetylene with small amounts of a powerful reductant? Explain your answers.
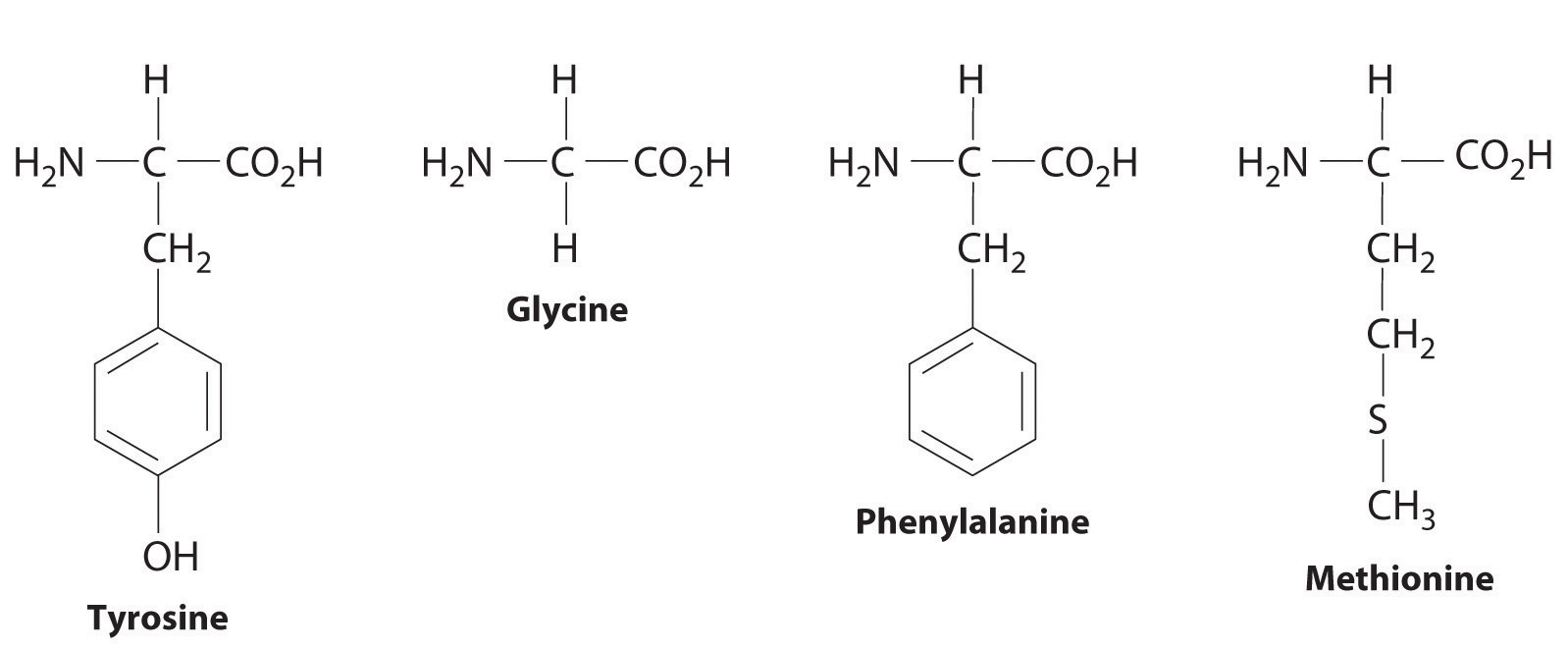
8. Enkephalins are pentapeptides, short biopolymers that are synthesized by humans to control pain. Enkephalins bind to certain receptors in brain cells, which are also known to bind morphine and heroin. One enkephalin has the structure tyrosine–glycine–glycine–phenylalanine–methionine. Draw its structure.
9. A polymerization reaction is used to synthesize Saran, a flexible material used in packaging film and seat covers. The monomeric unit for Saran is 1,1-dichloroethylene (CH2=CCl2), also known as vinylidene chloride. Draw a reasonable structure for the polymer. Why do pieces of Saran “cling” to one another when they are brought in contact?
10. Polymers are often amorphous solids. Like other materials, polymers can also undergo phase changes. For example, many polymers are flexible above a certain temperature, called the glass-transition temperature (Tg). Below the glass transition temperature, the polymer becomes hard and brittle. Biomedical devices that replace or augment parts of the human body often contain a wide variety of materials whose properties must be carefully controlled.
- Polydimethylsiloxane has a Tg of −123°C, whereas poly(methylmethacrylate) has a Tg of 105°C. Which of these polymers is likely to be used in dentures, and which is likely to be used for soft-tissue replacement?
- If you were designing biomedical devices, which class of biomaterials (alloys, ceramics, or polymers) would you consider for finger joint replacements, eyeball replacements, windpipe replacements, shoulder joint replacements, and bridging bone fractures? Explain your answers.
Contributors and Attributions
- Anonymous