9: Chemical Bonding and Molecular Energy Levels
- Page ID
- 85059
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Foundation
Our basis for understanding chemical bonding and the structures of molecules is the electron orbital description of the structure and valence of atoms, as provided by quantum mechanics. We assume an understanding of the periodicity of the elements based on the nuclear structure of the atom and our deductions concerning valence based on electron orbitals.
Goals
Our model of valence describes a chemical bond as resulting from the sharing of a pair of electrons in the valence shell of the bonded atoms. This sharing allows each atom to complete an octet of electrons in its valence shell, at least in the sense that we count the shared electrons as belonging to both atoms. However, it is not clear that this electron counting picture has any basis in physical reality. What is meant, more precisely, by the sharing of the electron pair in a bond, and why does this result in the bonding of two atoms together? Indeed, what does it mean to say that two atoms are bound together? Furthermore, what is the significance of sharing a pair of electrons? Why aren't chemical bonds formed by sharing one or three electrons, for example?
We seek to understand how the details of chemical bonding are related to the properties of the molecules formed, particularly in terms of the strengths of the bonds formed.
Observation 1: Bonding with a Single Electron
We began our analysis of the energies and motions of the electrons in atoms by observing the properties of the simplest atom, hydrogen, with a single electron. Similarly, to understand the energies and motions of electrons which lead to chemical bonding, we begin our observations with the simplest particle with a chemical bond, which is the \(\ce{H_2^+}\) molecular ion. Each hydrogen nucleus has a charge of +1. An \(\ce{H_2^+}\) molecular ion therefore has a single electron. It seems inconsistent with our notions of valence that a single electron, rather than an electron pair, can generate a chemical bond. However, these concepts have been based on observations on molecules, not molecular ions like \(\ce{H_2^+}\). And it is indeed found that \(\ce{H_2^+}\) is a stable bound molecular ion.
What forces and motions hold the two hydrogen nuclei close together in the \(\ce{H_2^+}\) ion? It is worth keeping in mind that the two nuclei must repel one another, since they are both positively charged. In the absence of the electron, the two nuclei would accelerate away from one another, rather than remaining in close proximity. What is the role of the electron? Clearly, the electron is attracted to both nuclei at the same time, and, in turn, each nucleus is attracted to the electron. The effect of this is illustrated in Figure 9.1. In Figure 9.1a, the electron is "outside" of the two nuclei. In this position, the electron is primarily attracted to the nucleus on the left, to which it is closer. More importantly, the nucleus on the right feels a greater repulsion from the other nucleus than attraction to the electron, which is farther away. As a result, the nucleus on the right experiences a strong force driving it away from the hydrogen atom on the left. This arrangement does not generate chemical bonding, therefore. By contrast, in Figure 9.1b, the electron is between the two nuclei. In this position, the electron is roughly equally attracted to the two nuclei, and very importantly, each nucleus feels an attractive force to the electron which is greater than the repulsive force generated by the other nucleus. Focusing on the electron's energy, the proximity of the two nuclei provides it a doubly attractive environment with a very low potential energy. If we tried to pull one of the nuclei away, this would raise the potential energy of the electron, since it would lose attraction to that nucleus. Hence, to pull one nucleus away requires us to add energy to the molecular ion. This is what is meant by a chemical bond: the energy of the electrons is lower when the atoms are in close proximity than when the atoms are far apart. This "holds" the nuclei close together, since we must do work (add energy) to take the nuclei apart.
a.
b. 
Figure 9.1: Electrostatic interactions in \(\ce{H_2^+}\). (a) When the electron is outside of the region between the two nuclei, the repulsion of the nuclei exceeds the attraction of the electron to the nuclei, and no bonding force is expected. (b) When the electron is in the region between the two nuclei, the attraction of the electron to the two nuclei exceeds the repulsion of the nuclei, lowering the total energy of the molecule and producing bonding.
Note that the chemical bond in Figure 9.1b results from the electron's position between the nuclei. On first thought, this appears to answer our question of what we mean by "sharing an electron pair" to form a chemical bond. An electrons positioned between two nuclei is "shared" to the extent that its potential energy is lowered due to attraction to both nuclei simultaneously.
On second thought, though, this description must be inaccurate. We have learned in our study of energy levels in atoms that an electron must obey the uncertainty principle and that, as a consequence, the electron does not have a definite position, between the nuclei or otherwise. We can only hope to specify a probability for observing an electron in a particular location. This probability is, from quantum mechanics, provided by the wave function. What does this probability distribution look like for the \(\ce{H_2^+}\) molecular ion?
To answer this question, we begin by experimenting with a distribution that we know: the \(1s\) electron orbital in a hydrogen atom. This we recall has the symmetry of a sphere, with equal probability in all directions away from the nucleus. To create an \(\ce{H_2^+}\) molecular ion from a hydrogen atom, we must add a bare second hydrogen nucleus (an \(\ce{H^+}\) ion). Imagine bringing this nucleus closer to the hydrogen atom from a very great distance (see Figure 9.2a). As the \(\ce{H^+}\) ion approaches the neutral atom, both the hydrogen atom's nucleus and electron respond to the electric potential generated by the positive charge. The electron is attracted and the hydrogen atom nucleus is repelled. As a result, the distribution of probability for the electron about the nucleus must become distorted, so that the electron has a greater probability of being near the \(\ce{H^+}\) ion and the nucleus has a greater probability of being farther from the ion. This distortion, illustrated in Figure 9.2b, is called "polarization": the hydrogen atom has become like a "dipole", with greater negative charge to one side and greater positive charge to the other.
a.
b.
c.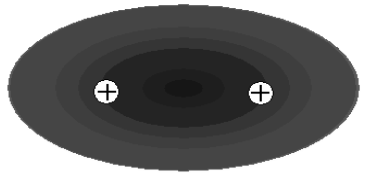
Figure 9.2: Polarization and bonding in \(\ce{H_2^+}\). (a) When the nuclei are separated to a great distance, the electron probability is described by a hydrogenic \(1s\) orbital, which is spherical. (b) As the bare nucleus approaches the hydrogen atom, the electron probability becomes "polarized" in the direction of the positive charge. (c) When the nuclei are close enough together, the electron probability is distributed equally over both nuclei, resulting in a "molecular orbital".
This polarization must increase as the \(\ce{H^+}\) ion approaches the hydrogen atom until, eventually, the electron orbital must be sufficiently distorted that there is equal probability for observing the electron in proximity to either hydrogen nucleus (see Figure 9.2c). The electron probability distribution in Figure 9.2c now describes the motion of the electron, not in a hydrogen atom, but in an \(\ce{H_2^+}\) molecular ion. As such, we refer to this distribution as a "molecular orbital".
We note that the molecular orbital in Figure 9.2c is more delocalized than the atomic orbital in Figure 9.2a, and this is also important in producing the chemical bond. We recall from the discussion of atomic energy levels that the energy of an electron in an orbital is determined, in part, by the compactness of the orbital. The more the orbital confines the motion of the electron, the higher is the kinetic energy of the electron, an effect we referred to as the "confinement energy". Applying this concept to the orbitals in Figure 9.2, we can conclude that the confinement energy is lowered when the electron is delocalized over two nuclei in a molecular orbital. This effect contributes significantly to the lowering of the energy of an electron resulting from sharing by two nuclei.
Recall that the electron orbitals in the hydrogen atom are described by a set of quantum numbers. One of these quantum numbers is related to the symmetry or shape of the atomic orbital and is generally depicted by a letter. Recall that an \(s\) orbital is spheric in shape, and a \(p\) orbital has two lobes aligned along one axis. Similarly, the molecular orbitals for the \(\ce{H_2^+}\) molecular ion are described by a set of numbers which give the symmetry (or shape) of the orbital. For our purposes, we need only one of these descriptors, based on the symmetry of the orbital along the bond: if the molecular orbital has the symmetry of a cylinder, we refer to it as a "\(\sigma\) orbital". The orbital in Figure 9.2c satisfies this condition.
We conclude that chemical bonding results from an electron in a molecular orbital which has substantial probability for the electron to be between two nuclei. However, this example illustrates chemical bonding with a single electron. Our rules of valence indicate that bonding typically occurs with a pair of electrons, rather than a single electron. Furthermore, this model of bonding does not tell us how to handle molecules with many electrons (say, \(\ce{F_2}\)) where most of the electrons do not participate in the bonding at all.
Observation 2: Bonding and Non-Bonding in Diatomic Molecules
We now consider molecules with more than one electron. These are illustrated most easily by diatomic molecules (molecules with only two atoms) formed by like atoms, beginning with the hydrogen molecule, \(\ce{H_2}\). The most direct experimental observation of a chemical bond is the amount of energy required to break it. This is called the bond energy, or somewhat less precisely, the bond strength. Experimentally, it is observed that the bond energy of the hydrogen molecule \(\ce{H_2}\) is \(458 \: \text{kJ/mol}\). By contrast, the bond energy of the \(\ce{H_2^+}\) molecular ion is \(269 \: \text{kJ/mol}\). Therefore, the bond in \(\ce{H_2}\) is stronger than the bond in \(\ce{H_2^+}\). Thus, the pair of shared electrons in \(\ce{H_2}\) generates a stronger attractive force than does the single electron in \(\ce{H_2^+}\).
Before deducing an explanation of this in terms of electron orbitals, we first recall the valence shell electron pair description of the bonding in \(\ce{H_2}\). Each hydrogen atom has a single electron. By sharing these two electrons, each hydrogen atom can fill its valence shell, attaining the electron configuration of helium.
How does this translate into the electron orbital picture of electron sharing that we have just described for the \(\ce{H_2^+}\) molecular ion? There are two ways to deduce the answer to this question, and, since they are both useful, we will work through them both. The first way is to imagine that we form an \(\ce{H_2}\) molecule by starting with an \(\ce{H_2^+}\) molecular ion and adding an electron to it. As a simple approximation, we might imagine that the first electron's probability distribution (its orbital) is not affected by the addition of the second electron. The second electron must have a probability distribution describing its location in the molecule as well. We recall that, in atoms, it is possible to put two electrons into a single electron orbital, provided that the two electrons have opposite values of the spin quantum number, \(m_s\). Therefore, we expect this to be true for molecules as well, and we place the added second electron in \(\ce{H_2}\) into the same \(\sigma\) orbital as the first. This results in two electrons in the region between the two nuclei, thus adding to the force of attraction of the two nuclei into the bond. This explains our observation that the bond energy of \(\ce{H_2}\) is almost (although not quite) twice the bond energy of \(\ce{H_2^+}\).
The second way to understand the electron orbital picture of \(\ce{H_2}\) is to imagine that we form the molecule by starting with two separated hydrogen atoms. Each of these atoms has a single electron in a \(1s\) orbital. As the two atoms approach one another, each electron orbital is polarized in the direction of the other atom. Once the atoms are close enough together, these two orbitals become superimposed. Now we must recall that these orbitals describe the wave-like motion of the electron, so that, when these two wave functions overlap, they must interfere, either constructively or destructively. In Figure 9.3, we see the consequences of constructive and destructive interference. We can deduce that, in \(\ce{H_2}\) the electron orbitals from the atoms must constructively interfere, because that would increase the electron probability in the region between the nuclei, resulting in bonding as before. Therefore, the \(\sigma\) molecular orbital describing the two electrons in \(\ce{H_2}\) can be understood as resulting from the constructive overlap of two atomic \(1s\) electron orbitals.
We now add to our observations of diatomic molecules by noting that, of the diatomic molecules formed from like atoms of the first ten elements, \(\ce{H_2}\), \(\ce{Li_2}\), \(\ce{B_2}\), \(\ce{C_2}\), \(\ce{N_2}\), \(\ce{O_2}\), and \(\ce{F_2}\) are stable molecules with chemical bonds, whereas \(\ce{He_2}\), \(\ce{Be_2}\), and \(\ce{Ne_2}\) are not bound. In examining the electron configurations of the atoms of these elements, we discover a correspondence with which diatomic molecules are bound and which ones are not. \(\ce{H}\), \(\ce{Li}\), \(\ce{B}\), \(\ce{N}\), and \(\ce{F}\) all have odd numbers of electrons, so that at least one electron in each atom is unpaired. By contrast, \(\ce{He}\), \(\ce{Be}\), and \(\ce{Ne}\) all have even numbers of electrons, none of which are unpaired. The other atoms, \(\ce{C}\) and \(\ce{O}\), both have an even number of electrons. However, as deduced in our understanding of the electron configurations in atoms, electrons will, when possible, distribute themselves into different orbitals of the same energy so as to reduce the effect of their mutual repulsion. Thus, in \(\ce{C}\) and \(\ce{O}\), there are three \(2p\) orbitals into which 2 and 4 electrons are placed, respectively. Therefore, in both atoms, there are two unpaired electrons. We conclude that bonds will form between atoms if and only if there are unpaired electrons in these atoms.
In \(\ce{H_2}\), the unpaired electrons from the separated atoms become paired in a molecular orbital formed from the overlap of the \(1s\) atomic electron orbitals. In the case of a hydrogen atom, then, there are of course no paired electrons in the atom to worry about. In all other atoms, there certainly are paired electrons, regardless of whether there are or are not unpaired electrons. For example, in a lithium atom, there are two paired electrons in a \(1s\) orbital and an unpaired electron in the \(2s\) orbital. To form \(\ce{Li_2}\), the unpaired electron from each atom can be placed into a molecular orbital formed from the overlap of the \(2s\) atomic electron orbitals. However, what becomes of the two electrons paired in the \(1s\) orbital in a \(\ce{Li}\) atom during the bonding of \(\ce{Li_2}\)?
To answer this question, we examine \(\ce{He_2}\), in which each atom begins with only the two \(1s\) electrons. As we bring the two \(\ce{He}\) atoms together from a large distance, these \(1s\) orbitals should become polarized, as in the hydrogen atom. When the polarized \(1s\) orbitals overlap, constructive interference will again result in a \(\sigma\) molecular orbital, just as in \(\ce{H_2}\). Yet, we observe that \(\ce{He_2}\) is not a stable bound molecule. The problem which prevents bonding for \(\ce{He_2}\) arises from the Pauli Exclusion Principle: only two of the four electrons in \(\ce{He_2}\) can be placed into this \(\sigma\) bonding molecular orbital. The other two must go into a different orbital with a different probability distribution. To deduce the form of this new orbital, we recall that the bonding orbital discussed so far arises from the constructive interference of the atomic orbitals, as shown in Figure 9.3. We could, instead, have assumed destructive interference of these orbitals. Destructive interference of two waves eliminates amplitude in the region of overlap of the waves, also shown in Figure 9.3. In the case of the atomic orbitals, this means that the molecular orbital formed from destructive interference decreases the probability for the electron to be in between the nuclei. Therefore, it increases probability for the electron to be outside the nuclei, as in Figure 9.1a. As discussed there, this arrangement for the electron does not result in bonding; instead, the nuclei repel each other and the atoms are forced apart. This orbital is thus called an anti-bonding orbital. This orbital also has the symmetry of a cylinder along the bond axis, so it is also a \(\sigma\) orbital; to indicate that it is an anti-bonding orbital, we designate it with an asterisk, \(\sigma^*\).
a.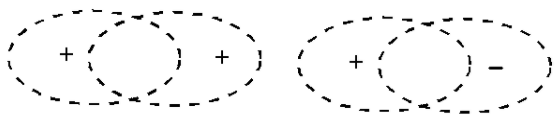
b.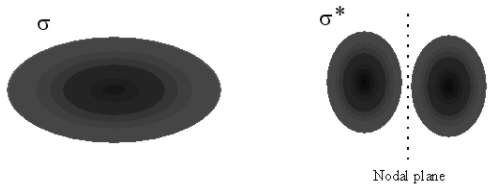
Figure 9.3: Formation of bonding and anti-bonding orbitals. (a) When two \(s\) orbitals overlap, they can interfere constructively (same sings) or destructively (different signs). (b) Constructive interference produces a bonding \(\sigma\) molecular orbital; destructive interference produces an antibonding \(\sigma^*\) molecular orbital, with a nodal plane between the nuclei.
In \(\ce{He_2}\), both the bonding and the anti-bonding orbitals must be used in order to accommodate four electrons. The two electrons in the bonding orbital lower the energy of the molecule, but the two electrons in the anti-bonding orbital raise it. Since two \(\ce{He}\) atoms will not bind together, then the net effect must be that the anti-bonding orbital more than offsets the bonding orbital.
We have now deduced an explanation for why the paired electrons in an atom do not contribute to bonding. Both bonding and anti-bonding orbitals are always formed when two atomic orbitals overlap. When the electrons are already paired in the atomic orbitals, then there are too many electrons for the bonding molecular orbital. The extra electrons must go into the anti-bonding orbital, which raises the energy of the molecule, preventing the bond from forming.
Returning to the \(\ce{Li_2}\) example discussed above, we can develop a simple picture of the bonding. The two \(1s\) electrons from each atom do not participate in the bonding, since the anti-bonding more than offsets the bonding. Thus, the paired "core" electrons remain in their atomic orbitals, unshared, and we can ignore them in describing the bond. The bond is formed due to overlap of the \(2s\) orbitals and sharing of these electrons only. This is also consistent with our earlier view that the core electrons are closer to the nucleus, and thus unlikely to be shared by two atoms.
The model we have constructed seems to describe fairly well the bonding in the bound diatomic molecules listed above. For example, in a fluorine atom, the only unpaired electron is in a \(2p\) orbital. Recall that a \(2p\) orbital has two lobes, directed along one axis. If these lobes are assumed to lie along the axis between the two nuclei in \(\ce{F_2}\), then we can overlap them to form a bonding orbital. Placing the two unpaired electrons into this orbital then results in a single shared pair of electrons and a stable molecular bond.
Observation 3: Ionization Energies of Diatomic Molecules
The energies of electrons in molecular orbitals can be observed directly by measuring the ionization energy. This is the energy required to remove an electron, in this case, from a molecule:
\[\ce{H_2} \left( g \right) \rightarrow \ce{H_2^+} \left( g \right) + \ce{e^-} \left( g \right)\]
The measured ionization energy of \(\ce{H_2}\) is \(1488 \: \text{kJ/mol}\). This number is primarily important in comparison to the ionization energy of a hydrogen atom, which is \(1312 \: \text{kJ/mol}\). Therefore, it requires more energy to remove an electron from the hydrogen molecule than from the hydrogen atom, so we can conclude that the electron has a lower energy in the molecule. If we attempt to pull the atoms apart, we must raise the energy of the electron. Hence, energy is required to break the bond, so the molecule is bound.
We conclude that a bond is formed when the energy of the electrons in the molecule is lower than the energy of the electrons in the separated atoms. This conclusion seems consistent with our previous view of shared electrons in bonding molecular orbitals.
As a second example, we consider the nitrogen molecule, \(\ce{N_2}\). We find that the ionization energy of molecular nitrogen is \(1503 \: \text{kJ/mol}\), and that of atomic nitrogen is \(1402 \: \text{kJ/mol}\). Once again, we conclude that the energy of the electrons in molecular nitrogen is lower than that of electrons in the separated atoms, so the molecule is bound.
As a third example, we consider fluorine, \(\ce{F_2}\). In this case, we find that the ionization energy of molecular fluorine is \(1515 \: \text{kJ/mol}\), which is smaller than the ionization energy of a fluorine atom, \(1681 \: \text{kJ/mol}\). This seems inconsistent with the bonding orbital concept we have developed above, which states that the electrons in the bond have a lower energy than in the separated atoms. If the electron being ionized has a higher energy in \(\ce{F_2}\) than in \(\ce{F}\), why is \(\ce{F_2}\) a stable molecule? Apparently, we need a more complete description of the molecular orbital concept of chemical bonding.
To proceed further, we compare bond energies in several molecules. Recall that the bond energy (or bond strength) is the energy required to separate the bonded atoms. We observe that the bond energy of \(\ce{N_2}\) is \(956 \: \text{kJ/mol}\). This is very much larger than the bond energy of \(\ce{H_2}\), \(458 \: \text{kJ/mol}\), and of \(\ce{F_2}\), which is \(160 \: \text{kJ/mol}\). We can account for the unusually strong bond in nitrogen using both our valence shell electron pair sharing model and our electron orbital descriptions. A nitrogen atom has three unpaired electrons in its valence shell, because the three \(2p\) electrons distribute themselves over the three \(2p\) orbitals, each oriented along a different axis. Each of these unpaired electrons is available for sharing with a second nitrogen atom. The result, from valence shell electron pair sharing concepts, is that three pairs of electrons are shared between two nitrogen atoms, and we called the bond in \(\ce{N_2}\) a "triple bond". It is somewhat intuitive that the triple bond in \(\ce{N_2}\) should be much stronger than the single bond in \(\ce{H_2}\) or in \(\ce{F_2}\).
Now consider the molecular orbital description of bonding in \(\ce{N_2}\). Each of the three \(2p\) atomic orbitals in each nitrogen atom must overlap to form a bonding molecular orbital, if we are to accommodate three electron pairs. Each \(2p\) orbital is oriented along a single axis. One \(2p\) orbital from each atom is oriented in the direction of the other atom, that is, along the bond axis. When these two atomic orbitals overlap, they form a molecular orbital which has the symmetry of a cylinder and which is therefore a \(\sigma\) orbital. Of course, they also form a \(\sigma^*\) orbital. The two electrons are then paired in the bonding orbital.
The other two \(2p\) orbitals on each nitrogen atom are perpendicular to the bond axis. The constructive overlap between these orbitals from different atoms must therefore result in a molecular orbital somewhat different than what we have discussed before. As shown in Figure 9.4, the molecular orbital which results now does not have the symmetry of a cylinder, and in fact, looks something more like a cylinder cut into two pieces. This we call a \(\pi\) orbital. There are two such \(\pi\) orbitals since there are two sets of \(p\) orbitals perpendicular to the bond axis. Figure 9.4 also shows that an anti-bonding orbital is formed from the destructive overlap of \(2p\) orbitals, and this is called a \(\pi^*\) orbital. There are also two \(\pi^*\) orbitals formed from destructive overlap of \(2p\) orbitals. In \(\ce{N_2}\), the three shared electron pairs are thus in a single \(\sigma\) orbital and in two \(\pi\) orbitals. Each of these orbitals is a bonding orbital, therefore all six electrons have their energy lowered in comparison to the separated atoms.
a.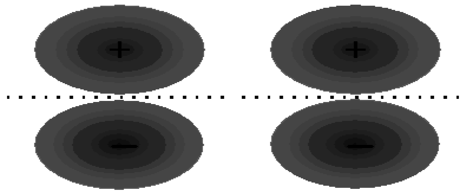
b.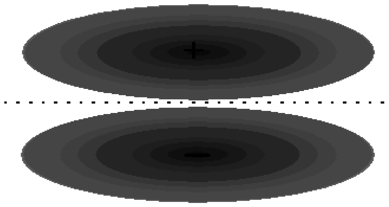
c.
Figure 9.4: \(\pi\) and \(\pi^*\) orbitals. (a) Two \(p\) orbitals perpendicular to the bond axis will overlap and interfere to produce \(\pi\) and \(\pi^*\) molecular orbitals. (b) Constructive interference results in formation of a bonding \(\pi\) molecular orbital. (c) Destructive interference results in formation of an anti-bonding \(\pi^*\) molecular orbital.
This is depicted in Figure 9.5 in what is called a "molecular orbital energy diagram". Each pair of atomic orbitals, one from each atom, is overlapped to form a bonding and an anti-bonding orbital. The three \(2p\) orbitals from each atom form one \(\sigma\) and \(\sigma^*\) pair and two \(\pi\) and \(\pi^*\) pairs. The lowering of the energies of the electrons in the \(\sigma\) and \(\pi\) orbitals is apparent. The ten \(n = 2\) electrons from the nitrogen atoms are then placed pairwise, in order of increasing energy, into these molecular orbitals. Note that, in agreement with the Pauli Exclusion Principle, each pair in a single orbital consists of one spin up and one spin down electron.
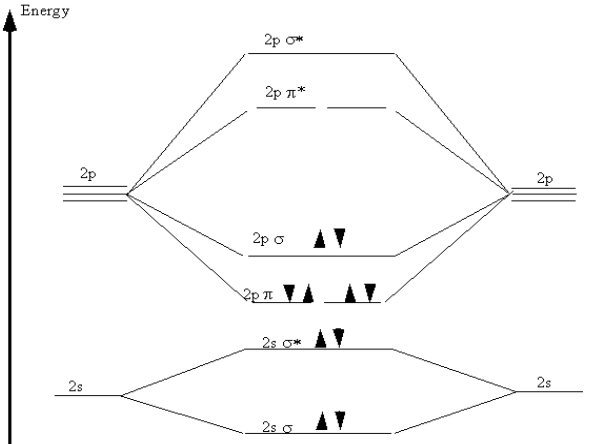
Figure 9.5: Molecular orbital energy diagram for nitrogen.
Recall now that we began the discussion of bonding in \(\ce{N_2}\) because of the curious result that the ionization energy of an electron in \(\ce{F_2}\) is less than that of an electron in an \(\ce{F}\) atom. By comparing the molecular orbital diagrams for \(\ce{N_2}\) and \(\ce{F_2}\) we are now prepared to answer this puzzle. There are five \(p\) electrons in each fluorine atom. These ten electrons must be distributed over the molecular orbitals whose energies are shown in Figure 9.6. (Note that the ordering of the bonding \(2p\) orbitals differ between \(\ce{N_2}\) and \(\ce{F_2}\).) We place two electrons in the \(\sigma\) orbitals, four more in the two \(\pi\) orbitals, and four more in the two \(\pi^*\) orbitals. Overall, there are six electrons in bonding orbitals and four in anti-bonding orbitals. Since \(\ce{F_2}\) is a stable molecule, we must conclude that the lowering of energy for the electrons in the bonding orbitals is greater than the raising of energy for the electrons in the antibonding orbitals. Overall, this distribution of electrons is, net, equivalent to having two electrons paired in a single bonding orbital.
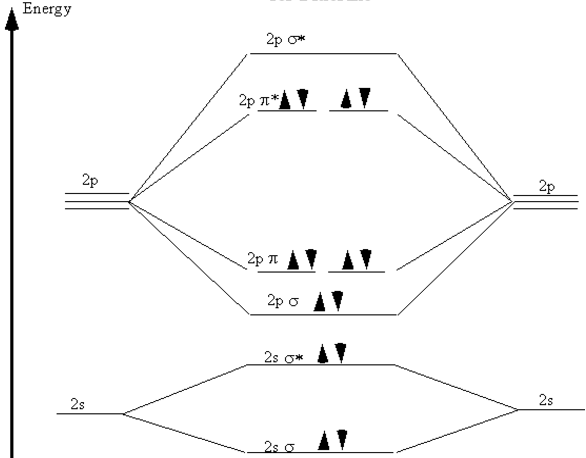
Figure 9.6: Molecular orbital energy diagram for fluorine.
This also explains why the ionization energy of \(\ce{F_2}\) is less than that of an \(\ce{F}\) atom. The electron with the highest energy requires the least energy to remove from the molecule or atom. The molecular orbital energy diagram in Figure 9.6 clearly shows that the highest energy electrons in \(\ce{F_2}\) are in anti-bonding orbitals. Therefore, one of these electrons is easier to remove than an electron in an atomic \(2p\) orbital, because the energy of an anti-bonding orbital is higher than that of the atomic orbitals. (Recall that this is why an anti-bonding orbital is, indeed, anti-bonding.) Therefore, the ionization energy of molecular fluorine is less than that of atomic fluorine. This clearly demonstrates the physical reality and importance of the anti-bonding orbitals.
A particularly interesting case is the oxygen molecule, \(\ce{O_2}\). In completing the molecular orbital energy level diagram for oxygen, we discover that we must decide whether to pair the last two electrons in the same \(2p\) \(\pi^*\) orbital, or whether they should be separated into two different \(2p\) \(\pi^*\) orbitals. To determine which, we note that oxygen molecules are paramagnetic, meaning that they are strongly attracted to a magnetic field. To account for this paramagnetism, we recall that electron spin is a magnetic property. In most molecules, all electrons are paired, so for each "spin up" electron there is a "spin down" electron and their magnetic fields cancel out. When all electrons are paired, the molecule is diamagnetic, meaning that it responds only weakly to a magnetic field.
If the electrons are not paired, they can adopt the same spin in the presence of a magnetic field. This accounts for the attraction of the paramagnetic molecule to the magnetic field. Therefore, for a molecule to be paramagnetic, it must have unpaired electrons. The correct molecular orbital energy diagram for an \(\ce{O_2}\) molecule is shown in Figure 9.7.
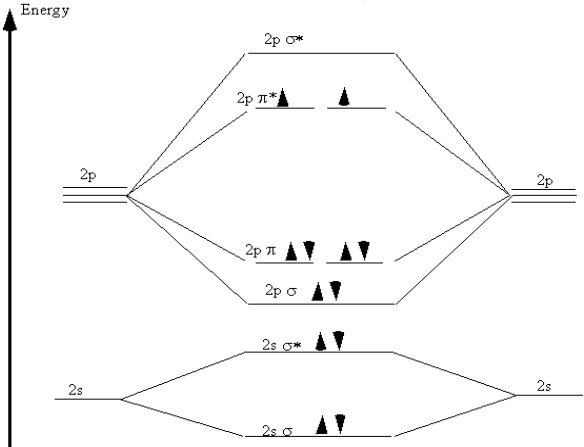
Figure 9.7: Molecular orbital energy diagram for oxygen.
In comparing these three diatomic molecules, we recall that \(\ce{N_2}\) has the strongest bond, followed by \(\ce{O_2}\) and \(\ce{F_2}\). We have previously accounted for this comparison with Lewis structures, showing that \(\ce{N_2}\) is a triple bond, \(\ce{O_2}\) is a double bond, and \(\ce{F_2}\) is a single bond. The molecular orbital energy level diagrams in Figures 9.5 to 9.7 cast a new light on this analysis. Note that, in each case, the number of bonding electrons in these molecules is eight. The difference in bonding is entirely due to the number of antibonding electrons: 2 for \(\ce{N_2}\), 4 for \(\ce{O_2}\), and 6 for \(\ce{F_2}\). Thus, the strength of a bond must be related to the relative numbers of bonding and antibonding electrons in the molecule. Therefore, we now define the bond order as
\[\text{Bond order} = \frac{1}{2} \left( \text{# bonding electrons} - \text{# antibonding electrons} \right)\]
Note that, defined this way, the bond order for \(\ce{N_2}\) is 3, for \(\ce{O_2}\) is 2, and for \(\ce{F_2}\) is 1, which agrees with our conclusions from Lewis structures. We conclude that we can predict the relative strengths of bonds by comparing bond orders.
Review and Discussion Questions
Why does an electron shared by two nuclei have a lower potential energy than an electron on a single atom? Why does an electron shared by two nuclei have a lower kinetic energy than an electron on a single atom? How does this sharing result in a stable molecule? How can this affect be measured experimentally?
Explain why the bond in an \(\ce{H_2}\) molecule is almost twice as strong as the bond in the \(\ce{H_2^+}\) ion. Explain why the \(\ce{H_2}\) bond is less than twice as strong as the \(\ce{H_2^+}\) bond.
\(\ce{Be_2}\) is not a stable molecule. What information can we determine from this observation about the energies of molecular orbitals?
Less energy is required to remove an electron from an \(\ce{F_2}\) molecule than to remove an electron from an \(\ce{F}\) atom. Therefore, the energy of that electron is higher in the molecule than in the atom. Explain why, nevertheless, \(\ce{F_2}\) is a stable molecule, i.e., the energy of an \(\ce{F_2}\) molecule is less than the energy of two \(\ce{F}\) atoms.
Why do the orbitals of an atom "hybridize" when forming a bond?
Calculate the bond orders of the following molecules and predict which molecule in each pair has the stronger bond:
1. \(\ce{C_2}\) or \(\ce{C_2^+}\)
2. \(\ce{B_2}\) or \(\ce{B_2^+}\)
3. \(\ce{F_2}\) or \(\ce{F_2^-}\)
4. \(\ce{O_2}\) or \(\ce{O_2^+}\)
Which of the following diatomic molecules are paramagnetic: \(\ce{CO}\), \(\ce{Cl_2}\), \(\ce{NO}\), \(\ce{N_2}\)?
\(\ce{B_2}\) is observed to be paramagnetic. Using this information, draw an appropriate molecular orbital energy level diagram for \(\ce{B_2}\).
Contributors and Attributions
John S. Hutchinson (Rice University; Chemistry)

