5: Quantum Energy Levels in Atoms
- Page ID
- 84788
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Foundation
The atomic molecular theory provides us a particulate understanding of matter. Each element is characterized as consisting of identical, indestructible atoms with atomic weights which have been determined. Compounds consists of identical molecules, each made up from a specific number of atoms of each of the component elements. We also know that atoms have a nuclear structure, meaning that all of the positive charge and virtually all of the mass of the atom are concentrated in a nucleus which is a very small fraction of the volume of the atom. Finally, we know that the electrons in the atom are arranged in "shells" about the nucleus, with each shell farther from the nucleus than the previous. The electrons in outer shells are more weakly attached to the atom than the electrons in the inner shells, and only a limited number of electrons can fit in each shell.
Goals
The shell model of the atom is a good start in understanding the differences in the chemical properties of the atoms of different elements. For example, we can understand the periodicity of chemical and physical properties from our model, since elements in the same group have the same number of electrons in the valence shell.
However, there are many details missing from our description. Other than a very crude calculation of "distance" of the shells from the nucleus, we have no description of what the differences are between the electrons in different shells. What precisely is a "shell"?
Most importantly, the arrangement of elements into groups and the periodicity of chemical properties both depend on the concept that a shell is "filled" by a certain number of electrons. Looking at the number of elements in each period, the number of electrons which fills a shell depends on which shell is being filled. In some cases, a shell is filled by eight electrons, in others, it appears to be 18 electrons. What determines how many electrons can "fit" in a shell? Why is there a limit at all?
Finally, a closer look at the ionization energies in Figure 4.3 reveals that our shell model must be incomplete. Our model implies that the elements of the second period from Lithium to Neon have their valence electrons in the second shell. With increasing nuclear charge, the ionization energy of these atoms should increase from Lithium to Neon. As a general trend, this is true, but there are variations. Note that the ionization energy of Oxygen atoms is less than that of Nitrogen atoms. We need to pursue addition detail in our model of the structure of the atom.
Observation 1: The Spectrum of Hydrogen
To begin, we need to know a little about light. All forms of electromagnetic radiation travel as an oscillating wave, with an electric field component perpendicular to a magnetic field component. As a wave, the radiation can be characterized by its "wavelength", symbolized as \(\lambda\), which is the distance between adjacent peaks in the wave. Different wavelengths correspond to different forms of electromagnetic radiation. For example, microwave radiation has wavelength in the range of \(10^{-2}\) to \(10^{-3}\) meters, whereas x-ray radiation has wavelength in the range \(10^{-9}\) to \(10^{-10}\) meters. Radiation which is visible to the human eye has wavelength in the very narrow range from \(3.8 \times 10^{7}\) to \(7.8 \times 10^{-7}\) meters.
Radiation can also be characterized by the frequency of the electromagnetic wave, which is the number of peaks in the wave which pass a point in space per second. Frequency is symbolized by \(\nu\). The speed which light travels in a vacuum is the same for all forms of electromagnetic radiation, \(c = 2.997 \times 10^8 \: \frac{\text{m}}{\text{s}}\). As such, we can relate the frequency of light to the wavelength of light by the equation
\[\lambda \left( \text{m} \right) \times \nu \left( \text{s}^{-1} \right) = c \left( \frac{\text{m}}{\text{s}} \right)\]
The longer the wavelength \(\lambda\), the lower the frequency \(\nu\). This makes sense when we remember that light travels at a fixed speed. When the wavelength is longer, fewer peaks will pass a point in space in a second. From this equation, there is a specific relationship between frequency and wavelength, and either or both can be used to characterize the properties of radiation.
With this background in hand, we can use our understanding of light to pursue more data about the energies of electrons in atoms. Ionization energies tell us how much energy is required to remove an electron from an atom, but do not tell us what happens if an electron changes its energy in an atom. To analyze this, we need a means to measure the energies gained or lost by an atom. One way to do so is to analyze the "spectrum" of an atom, which is the set of frequencies of light emitted by the atom. Since hydrogen is the simplest atom, we analyze the hydrogen spectrum first. We find that, if we pass a current of electricity through a sample of hydrogen gas, light is emitted. Careful analysis shows that, although some of this light is emitted by \(\ce{H_2}\) molecules, some of the light is also emitted by \(\ce{H}\) atoms. Since the light is a form of energy, then these \(\ce{H}\) atoms must release energy supplied to them by the electrons in the current.
Most importantly, if we pass the light emitted by the hydrogen gas sample through a prism, we can separate the colors as in a rainbow, each with a characteristic frequency. The resultant image of separated colors is called the spectrum of hydrogen. We find in this experiment that there are only four frequencies (four colors) of light in the emission that are visible. The most intense of the lines in the spectrum is bright red, but there are blue and violet lines. It turns out that there are also many other frequencies of light emitted which are invisible to the human eye.
Careful observation and analysis reveals that every frequency in the hydrogen atom spectrum can be predicted by a very simple formula, called the Rydberg equation:
\[\nu = R \times \left( \frac{1}{n^2} - \frac{1}{m^2} \right)\]
where \(R\) is the Rydberg constant \(\left( 3.29 \times 10^{15} \: \text{s}^{-1} \right)\). \(n\) and \(m\) are integers (1,2,3,...). Each choice of \(n\) and \(m\) predicts a single observed frequency in the hydrogen atom spectrum.
The atoms of all elements emit radiation when energized in an electric current, and as do all molecules of all compounds. However, we find that the specific frequencies of light emitted are characteristic of each atom or molecule. In other words, the spectrum of each element is unique to each element or compound. As a result, the spectrum of each substance can be used to identify that substance. (Note that the Rydberg equation tells us only the spectrum of hydrogen.)
Our interest is in the fact that the radiation emitted by an atom tells us about the amounts of energy which can be released by an atom. For a hydrogen atom, for example, these changes in energy must correspond to the amounts of energy which the electrons inside the atom can gain or lose.
At this point, we need to relate the frequency of radiation emitted by an atom to the amount of energy lost by the electron in the atom. We thus examine some observations about the energy of radiation.
Observation 2: The Photoelectric Effect
When a light source is directed at a metal surface, it is found under many circumstances that electrons are ejected from the surface. This phenomenon is called the "photoelectric effect". These electrons can be collected to produce a usable electric current. (This effect has a variety of common practical applications, for example, in "electric eye" devices.) It is reasonable to expect that a certain amount of energy is required to liberate an electron from a metal surface, since the electron is attracted to the positively charged nuclei in the metal. Thus, in order for the electron to escape, the light must supply sufficient energy to the electron to overcome this attraction.
The following experimental observations are found when studying the photoelectric effect. First, in order for the effect to be observed, the light must be of at least a minimum frequency which we call the threshold frequency, \(\nu_0\). This frequency is characteristic for a given metal. That is, it is the same value for each sample of that metal, but it varies from one metal to the next. For low frequency light, photoelectrons are not observed in any number, no matter how intense the light source is. For light with frequency above \(\nu_0\), the number of photoelectrons emitted by the metal (measured by the photoelectric current, \(\Phi\)) increases directly with the intensity of the light. These results are shown in Figure 5.1.
The Photoelectric Effect
a.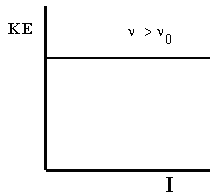 b.
b.
Figure 5.1: \(\Phi\) is the photoelectric current, \(\nu\) is the frequency of incident light, and \(I\) is the intensity of incident light. (a) For photoelectrons to be emitted, the light frequency must be greater than a threshold value. (b) If the frequency is high enough, the number of photoelectrons increases directly with the light intensity.
Second, we can measure the energies of the electrons emitted by the metal. For a given metal, all photoelectrons have the same kinetic energy for a fixed frequency of light above \(\nu_0\). This fixed kinetic energy is independent of the intensity of the light source. As the frequency of the light is increased, the kinetic energy of the emitted electrons increases proportionally. These results are shown in Figure 5.2.
More Photoelectric Effect
a.  b.
b. 
Figure 5.2: \(KE\) is the photoelectron kinetic energy, \(\nu\) is the frequency of incident light, and \(I\) is the intensity of incident light. (a) If the frequency is high enough, the energy of the electrons increases directly with the frequency. (b) However, the energy of the photoelectrons does not depend on the light intensity.
Are these results surprising? To the physicists at the end of the nineteenth century, the answer was yes, very surprising indeed. They expected that the energy of the light source should be determined by its intensity. Hence, the energy required to eject a photoelectron should be supplied by light of high intensity, no matter how low the frequency of the radiation. Thus, there should be no threshold frequency, below which no electrons are emitted. Moreover, the kinetic energy of the electrons should increase with intensity, not with light frequency. These predictions are not observed, so the results are counter to physical intuition.
We can account for these results in a straightforward but perhaps non-obvious manner. (Einstein provided the explanation in 1905.) Since the kinetic energy of the emitted photoelectrons increases proportionally with increases in the frequency of the light above the threshold frequency, we can conclude from conservation of total energy that the energy supplied by the light to the ejected electron must be proportional to its frequency: \(E \propto \nu\). This does not immediately account for the existence of the threshold frequency, though, since it would still seem to be the case that even low frequency light would possess high energy if the intensity were sufficient. By this reasoning, high intensity, low frequency light should therefore produce as many photoelectrons as are produced by low intensity, high frequency light. But this is not observed.
This is a very challenging puzzle, and an analogy helps to reveal the subtle answer. Imagine trying to knock pieces out of a wall by throwing objects at it. We discover that, no matter how many ping pong balls we throw, we cannot knock out a piece of the wall. On the other hand, only a single bowling ball is required to accomplish the task. The results of this "experiment" are similar to the observations of the photoelectric effect: very little high frequency light can accomplish what an enormous amount of low frequency light cannot. The key to understanding our imaginary experiment is knowing that, although there are many more ping pong balls than bowling balls, it is only the impact of each individual particle with the wall which determines what happens.
Reasoning from this analogy, we must conclude that the energy of the light is supplied in "bundles" or "packets" of constant energy, which we will call photons. We have already concluded that the light supplies energy to the electron which is proportional to the light frequency. Now we can say that the energy of each photon is proportional to the frequency of the light. The intensity of the light is proportional to the number of these packets. This now accounts for the threshold frequency in a straightforward way. For a photon to dislodge a photoelectron, it must have sufficient energy, by itself, to supply to the electron to overcome its attraction to the metal. Although increasing the intensity of the light does increase the total energy of the light, it does not increase the energy of an individual photon. Therefore, if the frequency of the light is too low, the photon energy is too low to eject an electron. Referring back to the analogy, we can say that a single bowling ball can accomplish what many ping pong balls cannot, and a single high frequency photon can accomplish what many low frequency photons cannot.
The important conclusion for our purposes is that light energy is quantized into packets of energy. The amount of energy in each photon is given by Einstein's equation,
\[E = h \nu\]
where \(h\) is a constant called Planck's constant.
Quantized Energy Levels in Hydrogen Atoms
We can combine the observation of the hydrogen atom spectrum with our deduction that light energy is quantized into packets to reach an important conclusion. Each frequency of light in the spectrum corresponds to a particular energy of light and, therefore, to a particular energy loss by a hydrogen atom, since this light energy is quantized into packets. Furthermore, since only certain frequencies are observed, then only certain energy losses are possible. This is only reasonable if the energy of each hydrogen atom is restricted to certain specific values. If the hydrogen atom could possess any energy, then it could lose any amount of energy and emit a photon of any energy and frequency. But this is not observed. Therefore, the energy of the electron in a hydrogen atom must be restricted to certain energy levels.
The Hydrogen atom spectrum also tells us what these energy levels are. Recall that the frequencies of radiation emitted by Hydrogen atoms are given by the Rydberg equation. Each choice of the positive integers \(n\) and \(m\) predicts a single observed frequency in the hydrogen atom spectrum.
Each emitted frequency must correspond to an energy \(h \nu\) by Einstein's equation. This photon energy must be the difference between two energy levels for a hydrogen electron, since that is the amount of energy released by the electron moving from one level to the other. If the energies of the two levels are \(E_m\) and \(E_n\), then we can write that
\[h \nu = E_m - E_n\]
By comparing this to the Rydberg equation, each energy level must be given by the formula
\[E_n = \left( -h \right) R \frac{1}{n^2}\]
We can draw two conclusions. First, the electron in a hydrogen atom can exist only with certain energies, corresponding to motion in what we now call a state or an orbital. Second, the energy of a state can be characterized by an integer quantum number, \(n = 1, 2, 3, ...\) which determines its energy.
These conclusions are reinforced by similar observations of spectra produced by passing a current through other elements. Only specific frequencies are observed for each atom, although only the hydrogen frequencies obey the Rydberg formula.
We conclude that the energies of electrons in atoms are "quantized", that is, restricted to certain values. We now need to relate this quantization of energy to the existence of shells, as developed in Module 4.
Observation 3: Photoelectron Spectroscopy of Multi-Electron Atoms
The ionization energy of an atom tells us the energy of the electron or electrons which are at highest energy in the atom and are thus easiest to remove from the atom. To further analyze the energies of the electrons more tightly bound to the nucleus, we introduce a new experiment. The photoelectric effect can be applied to ionize atoms in a gas, in a process often called photoionization. We shine light on an atom and measure the minimum frequency of light, corresponding to a minimum energy, which will ionize an electron from an atom. When the frequency of light is too low, the photons in that light do not have enough energy to ionize electrons from an atom. As we increase the frequency of the light, we find a threshold at which electrons begin to ionize. Above this threshold, the energy \(h \nu\) of the light of frequency \(\nu\) is greater than the energy required to ionize the atom, and the excess energy is retained by the ionized electron as kinetic energy.
In photoelectron spectroscopy, we measure the kinetic energy of the electrons which are ionized by light. This provides a means of measuring the ionization energy of the electrons. By conservation of energy, the energy of the light is equal to the ionization energy \(IE\) plus the kinetic energy \(KE\) of the ionized electron:
\[h \nu = IE + KE\]
Thus, if we use a known frequency \(n\) and measure \(KE\), we can determine \(IE\). The more tightly bound an electron is to the atom, the higher the ionization energy and the smaller the kinetic energy of the ionized electron. If an atom has more than one electron and these electrons have different energies, then for a given frequency of light, we can expect electrons to be ejected with different kinetic energies. The higher kinetic energies correspond to the weakly bound outer electrons, and the lower kinetic energies correspond to the tightly bound inner electrons.
The ionization energies for the first twenty elements are given in Table 5.1. We note that there is a single ionization energy for hydrogen and helium. This is consistent with the shell model of these atoms since, in both of these atoms, the electron or electrons are in the innermost shell. The energies of these electrons correspond to the \(n = 1\) energy level of the hydrogen atom. In lithium and beryllium, there are two ionization energies. Again, this is consistent with the shell model, since now there are electrons in both of the first two shells. Note also that the ionization energy of the inner shell electrons increases as we go from hydrogen to lithium to beryllium, because of the increase in nuclear charge. The lower energy electrons correspond to the \(n = 1\) energy level of hydrogen and the higher energy electrons correspond to the \(n = 2\) energy level.
Table 5.1: Ionization energies of the first twenty elements
| Element | Ionization Energy \(\left( \text{MJ/mol} \right)\) | |||||
| \(\ce{H}\) | 1.31 | |||||
| \(\ce{He}\) | 2.37 | |||||
| \(\ce{Li}\) | 6.26 | 0.52 | ||||
| \(\ce{Be}\) | 11.5 | 0.90 | ||||
| \(\ce{B}\) | 19.3 | 1.36 | 0.80 | |||
| \(\ce{C}\) | 28.6 | 1.72 | 1.09 | |||
| \(\ce{N}\) | 39.6 | 2.45 | 1.40 | |||
| \(\ce{O}\) | 52.6 | 3.12 | 1.31 | |||
| \(\ce{F}\) | 67.2 | 3.88 | 1.68 | |||
| \(\ce{Ne}\) | 84.0 | 4.68 | 2.08 | |||
| \(\ce{Na}\) | 104 | 6.84 | 3.67 | 0.50 | ||
| \(\ce{Mg}\) | 126 | 9.07 | 5.31 | 0.74 | ||
| \(\ce{Al}\) | 151 | 12.1 | 7.79 | 1.09 | 0.58 | |
| \(\ce{Si}\) | 178 | 15.1 | 10.3 | 1.46 | 0.79 | |
| \(\ce{P}\) | 208 | 18.7 | 13.5 | 1.95 | 1.01 | |
| \(\ce{S}\) | 239 | 22.7 | 16.5 | 2.05 | 1.00 | |
| \(\ce{Cl}\) | 273 | 26.8 | 20.2 | 2.44 | 1.25 | |
| \(\ce{Ar}\) | 309 | 31.5 | 24.1 | 2.82 | 1.52 | |
| \(\ce{K}\) | 347 | 37.1 | 29.1 | 3.93 | 2.38 | 0.42 |
| \(\ce{Ca}\) | 390 | 42.7 | 34.0 | 4.65 | 2.9 | 0.59 |
Surprisingly, though, boron has three ionization energies, which does not seem consistent with the shell model. From the hydrogen atom energy levels, we would have expected that all \(n = 2\) electrons would have the same energy. We can note that the two smaller ionization energies in boron are comparable in magnitude and smaller by more than a factor of ten than the ionization energy of the electrons in the inner shell. Thus, the electrons in the outer \(n = 2\) shell apparently have comparable energies, but they are not identical. The separation of the second shell into two groups of electrons with two comparable but different energies is apparent for elements boron to neon.
As such, we conclude from the experimental data that the second shell of electrons should be described as two subshells with slightly different energies. For historical reasons, these subshells are referred to as the "\(2s\)" and "\(2p\)" subshells, with \(2s\) electrons slightly lower in energy than \(2p\) electrons. The energies of the \(2s\) and \(2p\) electrons decrease from boron to neon, consistent with the increase in the nuclear charge.
Beginning with sodium, we observe four distinct ionization energies, and beginning with aluminum there are five. Note for these elements that the fourth and fifth ionization energies are again roughly a factor of ten smaller than the second and third ionization energies, which are in turn at least a factor of ten less than the first ionization energy. Thus, it appears that there are three shells of electrons for these atoms, consistent with our previous shell model. As with \(n = 2\), the \(n = 3\) shell is again divided into two subshells, now called the \(3s\) and \(3p\) subshells.
These data also reveal how many electrons can reside in each subshell. In each \(n\) level, there are two elements which have only the ionization energy for the \(s\) subshell. Hence, \(s\) subshells can hold two electrons. By contrast, there are 6 elements which have both the \(s\) and \(p\) subshell ionization energies, so the \(p\) subshell can hold 6 electrons.
The shell and subshell organization of electron energies can also be observed by measuring the "electron affinity" of the atoms. Electron affinity is the energy released when an electron is added to an atom:
\[\ce{A} \left( g \right) + \ce{e^-} \left( g \right) \rightarrow \ce{A^-} \left( g \right)\]
If there is a strong attraction between the atom \(\ce{A}\) and the added electron, then a large amount of energy is released during this reaction, and the electron affinity is a large positive number. (As a note, this convention is the opposite of the one usually applied for energy changes in reactions: exothermic reactions, which give off energy, conventionally have negative energy changes.)
The electron affinities of the halogens are large positive values: the electron affinities of \(\ce{F}\), \(\ce{Cl}\), and \(\ce{Br}\) are \(328.0 \: \text{kJ/mol}\), \(348.8 \: \text{kJ/mol}\), and \(324.6 \: \text{kJ/mol}\). Thus, the attached electrons are strongly attracted to the nucleus in each of these atoms. This is because there is room in the current subshell to add an additional electron, since each atom has 5 \(p\) electrons, and the core charge felt by the electron in that subshell is large.
By contrast, the electron affinities of the inert gases are negative: the addition of an electron to an inert gas atom actually requires the input of energy, in effect, to force the electron into place. This is because the added electron cannot fit in the current subshell and must be added to a new shell, farther from the nucleus. As such, the core charge felt by the added electron is very close to zero.
Similarly, the electron affinities of the elements \(\ce{Be}\), \(\ce{Mg}\), and \(\ce{Ca}\) are all negative. This is again because the \(s\) subshell in these atoms already has two electrons, so the added electron must go into a higher energy subshell with a much smaller core charge.
Electron Waves, the Uncertainty Principle, and Electron Energies
We now have a fairly detailed description of the energies of the electrons in atoms. What we do not have is a model which tells us what factors determine the energy of an electron in a shell or subshell. Nor do we have a model to explain why these energies are similar but different for electrons in different subshells.
A complete answer to these questions requires a development of the quantum theory of electron motion in atoms. Because the postulates of this quantum theory cannot be readily developed from experimental observations, we will concern ourselves with a few important conclusions only.
The first important conclusion is that the motion of an electron in an atom is described by a wave function. Interpretation of the wave motion of electrons is a very complicated proposition, and we will only deal at present with a single important consequence, namely the uncertainty principle. A characteristic of wave motion is that, unlike a particle, the wave does not have a definite position at a single point in space. By contrast, the location of a particle is precise. Therefore, since an electron travels as a wave, we must conclude that we cannot determine the precise location of the electron in an atom. This is, for our purposes, the uncertainty principle of quantum mechanics. We can make measurements of the location of the electron, but we find that each measurement results in a different value. We are then forced to accept that we cannot determine the precise location. We are allowed, however, to determine a probability distribution for where the electron is observed.
This probability distribution is determined by quantum mechanics. The motion of the electron in a hydrogen atom is described by a function, often called the wave function or the electron orbital and typically designated by the symbol \(\Psi\). \(\Psi\) is a function of the position of the electron \(r\), and quantum mechanics tells us that \(\left( \left| \Psi \right| \right)^2\) is the probability of observing the electron at the location \(r\).
Each electron orbital has an associated constant value of the electronic energy, \(\ce{E_n}\), in agreement with our earlier conclusions. In fact, quantum mechanics exactly predicts the energy shells and the hydrogen atom spectrum we observe. The energy of an electron in an orbital is determined primarily by two characteristics of the orbital. The first, rather intuitive, property determines the average potential energy of the electron: an orbital which has substantial probability in regions of low potential energy will have a low total energy. By Coulomb's law, the potential energy arising from nucleus-electron attraction is lower when the electron is nearer the nucleus. In atoms with more than one electron, electron-electron repulsion also contributes to the potential energy, as Coulomb's law predicts an increase in potential energy arising from the repulsion of like charges.
A second orbital characteristic determines the contribution of kinetic energy, via a more subtle effect arising out of quantum mechanics. As a consequence of the uncertainty principle, quantum mechanics predicts that, the more confined an electron is to a smaller region of space, the higher must be its average kinetic energy. Since we cannot measure the position of the electron precisely, we define the uncertainty in the measurement as \(\Delta \left( x \right)\). Quantum mechanics also tells us that we cannot measure the momentum of an electron precisely either, so there is an uncertainty \(\Delta \left( p \right)\) in the momentum. In mathematical detail, the uncertainty principle states that these uncertainties are related by an inequality:
\[\Delta \left( x \right) \Delta \left( p \right) \ge \frac{h}{4 \pi}\]
where \(h\) is Planck's constant, \(6.62 \times 10^{-34} \: \text{J} \cdot \text{s}\) (previously seen in Einstein's equation for the energy of a photon). This inequality reveals that, when an electron moves in a small area with a correspondingly small uncertainty \(\Delta \left( x \right)\), the uncertainty in the momentum \(\Delta \left( p \right)\) must be large. For \(\Delta \left( p \right)\) to be large, the momentum must also be large, and so must be the kinetic energy.
Therefore, the more compact an orbital is, the higher will be the average kinetic energy of an electron in that orbital. This extra kinetic energy, which can be regarded as the confinement energy, is comparable in magnitude to the average potential energy of electron-nuclear attraction. Therefore, in general, an electron orbital provides a compromise, somewhat localizing the electron in regions of low potential energy but somewhat delocalizing it to lower its confinement energy.
Electron Orbitals and Subshell Energies
We need to account for the differences in energies of the electrons in different subshells, since we know that, in a Hydrogen atom, the orbital energy depends only on the \(n\) quantum number. We recall that, in the Hydrogen atom, there is a single electron. The energy of that electron is thus entirely due to its kinetic energy and its attraction to the nucleus. The situation is different in all atoms containing more than one electron, because the energy of the electrons is affected by their mutual repulsion. This repulsion is very difficult to quantify, but our model must take it into account.
A simple way to deal with the effect of electron-electron repulsion is to examine the shell structure of the atom. The two \(n = 1\) electrons in beryllium are in a shell with a comparatively short average distance from the nucleus. Therefore, the two \(n = 2\) electrons are in a shell which is, on average, "outside" of the \(n = 1\) shell. The \(n = 1\) electrons are thus the "core" and the \(n = 2\) electrons are in the valence shell. This structure allows us to see in a simple way the effect of electron-electron repulsion on the energies of the \(n = 2\) electrons. Each \(n = 2\) electron is attracted by the +4 charge on the tiny beryllium nucleus, but is repelled by the two -1 charges from the inner shell formed by the two \(n = 1\) electrons. Net, then, an \(n = 2\) electron effectively "sees" roughly a +2 nuclear charge. We refer to this +2 as the "core charge" since it is the net charge on the core resulting from the balance of attraction to the nucleus and repulsion from the core electrons. The nucleus is partially "shielded" from the valence electrons by the core electrons.
This shielding effect does not seem to account for the difference in ionization energies between the \(2s\) and \(2p\) or for the lower ionization energy of boron compared to beryllium, since, in each atom, the valence electrons are in the \(n = 2\) shell. However, the shielding effect is not perfect. Recall that we only know the probabilities for observing the positions of the electrons. Therefore, we cannot definitely state that the \(n = 2\) electrons are outside of the \(n = 1\) core. In fact, there is some probability that an \(n = 2\) electron might be found inside the \(n = 1\) core, an effect called "core penetration". When an \(n = 2\) electron is very strongly attracted to the nucleus and its energy is thus lowered. What is the extent of this penetration? We must consult quantum theory. The answer is in Figure 5.3, which shows the probability of finding an electron a distance \(r\) away from the nucleus for each of the \(1s\), \(2s\), and \(2p\) orbitals. We can see that there is a greater probability (though small) for the \(2s\) electron to penetrate the core than for the \(2p\) electron to do so.

Figure 5.3: Probability for an electron at a distance \(r|) from a hydrogen nucleus
As a result of the core penetration, an electron in a \(2s\) orbital feels a greater "effective nuclear charge" than just the core charge, which was approximated by assuming perfect shielding. Thus the effective nuclear charge for a \(2s\) electron is greater than the effective nuclear charge for a \(2p\) electron. Therefore, the energy of an electron in the \(2s\) orbital in beryllium is lower than it would be in the \(2p\) orbital.
A detailed analysis from quantum mechanics gives the following ordering of orbitals in order of increasing energy:
\[1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < \ldots\]
This ordering can be rationalized on the basis of effective nuclear charge, shielding, and core penetration.
Review and Discussion Questions
The photoelectric effect demonstrates that radiation energy is quantized into "packets" or photons. Explain how and why this observation is of significance in understanding the structure of atoms.
Explain how we can know that higher frequency light contains higher energy photons.
Electron affinity is the energy released when an electron is attached to an atom. If an atom has a positive electron affinity, the added electron is attracted to the nucleus to form a stable negative ion. Why doesn't a Beryllium atom have a positive electron affinity? Explain how this demonstrates that the energy of a \(2s\) orbital is less than the energy of a \(2p\) orbital.
Why does an inert gas atom have a high ionization energy but a low electron affinity? Why do these properties combine to make the atoms of inert gases unreactive?
Consider electrons from two different subshells in the same atom. In photoelectron spectroscopy, the lower energy electron has a higher ionization energy but is observed to have lower kinetic energy after ionization. Reconcile the lower kinetic energy with the higher ionization energy.
Chlorine atoms have 5 distinct ionization energies. Explain why. Predict the number of ionization energies for Bromine atoms, and explain you answer. (Hint: examine the structure of the periodic table.)
Why does a Bromine atom have a much smaller radius than a Potassium atom, even though a \(\ce{Br}\) atom has 16 more electrons than does a \(\ce{K}\) atom?
Explain why electrons confined to smaller orbitals are expected to have higher kinetic energies.
Define "shielding" in the context of electron-electron repulsion. What is the significance of shielding in determining the energy of an electron? How is this affected by core penetration?
Contributors and Attributions
John S. Hutchinson (Rice University; Chemistry)

