4: The Structure of an Atom
- Page ID
- 84785
Foundation
We begin as a starting point with the atomic molecular theory. We thus assume that most of the common elements have been identified, and that each element is characterized as consisting of identical, indestructible atoms. We also assume that the atomic weights of the elements are all known, and that, as a consequence, it is possible via mass composition measurements to determine the molecular formula for any compound of interest. In addition, we will assume that it has been shown by electrochemical experiments that atoms contain equal numbers of positively and negatively charged particles, called protons and electrons respectively. Finally, we assume an understanding of the Periodic Table. In particular, we assume that the elements can be grouped according to their common chemical and physical properties, and that these chemical and physical properties are periodic functions of the atomic number.
Goals
The atomic molecular theory is extremely useful in explaining what it means to form a compound from its component elements. That is, a compound consists of identical molecules, each comprised of the atoms of the component elements in a simple whole number ratio. However, our knowledge of these atoms is very limited. The only property we know at this point is the relative mass of each atom. Consequently, we cannot answer a wide range of new questions. We need a model which accounts for the periodicity of chemical and physical properties as expressed in the Periodic Table. Why are elements which are very dissimilar in atomic mass nevertheless very similar in properties? Why do these common properties recur periodically?
We would like to understand what determines the number of atoms of each type which combine to form stable compounds. Why are some combinations found and other combinations not observed? Why do some elements with very dissimilar atomic masses (for example, iodine and chlorine) form very similar chemical compounds? Why do other elements with very similar atomic masses (for example, oxygen and nitrogen) form very dissimilar compounds? In general, what forces hold atoms together in forming a molecule?
Answering these questions requires knowledge of the structure of the atom, including how the structures of atoms of different elements are different. Our model should tell us how these structural differences result in the different bonding properties of the different atoms.
Observation 1: Scattering of \(\alpha\) particles by atoms
We have assumed that atoms contain positive and negative charges and the number of these charges is equal in any given atom. However, we do not know what that number is, nor do we know how those charges are arranged inside the atom. To determine the location of the charges in the atom, we perform a "scattering" experiment. The idea is straightforward: since we cannot "see" the atomic structure, then we instead "throw" things at the atom and watch the way in which these objects are deflected by the atom. Working backwards, we can then deduce what the structure of the atom must be.
The atoms we choose to shoot at are gold, in the form of a very thin gold foil of thickness about \(10^{-4} \: \text{cm}\). The objects we "throw" are actually \(\alpha\) particles, which are positively charged and fairly massive, emitted by radioactive polonium nuclei. The \(\alpha\) particles are directed in a very precise narrow line perpendicular to and in the direction of the gold foil. We then look for \(\alpha\) particles at various angles about the gold foil, looking both for particles which have been deflected as they pass through the foil or which have been reflected as they bounce off of the foil. The scattering experiment is illustrated below.
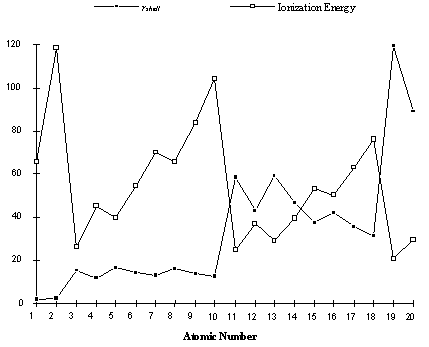
Figure 4.1: \(\alpha\) particle Scattering from Gold Foil
The result of the experiment is initially counter-intuitive. Most of the \(\alpha\) particles pass through the gold foil undeflected, as if there had been nothing in their path! A smaller number of the particles are deflected sharply as they pass through the foil, and a very small fraction of the \(\alpha\) particles are reflected backwards off of the gold foil. How can we simultaneously account for the lack of any deflection for most of the \(\alpha\) particles and for the deflection through large angles of a very small number of particles?
First, since the majority of the positively charged \(\alpha\) particles pass through the gold foil undeflected, we can conclude that most of the volume of each gold atom is empty space, containing nothing which might deflect an \(\alpha\) particle. Second, since a few of the positively charged \(\alpha\) particles are deflected very sharply, then they must encounter a positively charged massive particle inside the atom. We therefore conclude that all of the positive charge and most of the mass of an atom is contained in a nucleus. The nucleus must be very small, very massive, and positively charged if it is to account for the sharp deflections. A detailed calculation based assuming this model reveals that the nucleus must be about 100,000 times smaller than the size of the atom itself. The electrons, already known to be contained in the atom, must be outside of the nucleus, since the nucleus is positively charged. They must move in the remaining space of the much larger volume of the atom. Moreover, in total, the electrons comprise less than \(0.05\%\) of the total mass of an atom.
This model accounts for observation of both undeflected passage of most of the \(\alpha\) particles and sharp deflection of a few. Most \(\alpha\) particles pass through the vast empty space of the atom, which is occupied only by electrons. Even the occasional encounter with one of the electrons has no effect on an \(\alpha\) particle's path, since each \(\alpha\) particle is much more massive than an electron. However, the nucleus is both massive and positively charged, but it is also small. The rare encounter of an \(\alpha\) particle with the nucleus will result in very large deflections; a head-on collision with a gold atom nucleus will send an \(\alpha\) particle directly back to its source.
Observation 2: X-ray emission
Although we can now conclude that an atom has a nuclear structure, with positive charge concentrated in a very small nucleus and a number of electrons moving about the nucleus in a much larger volume, we do not have any information on how many electrons there are in an atom of any given element or whether this number depends on the type of atom. Does a gold atom have the same number of electrons as a silver atom? All we can conclude from the data given is that the number of positive charges in the nucleus must exactly equal the number of electrons moving outside the nucleus, since each atom is neutral. Our next difficulty is that we do not known what these numbers are.
The relevant observation seems unrelated to the previous observations. In this case, we examine the frequency of x-rays emitted by atoms which have been energized in an electrical arc. Each type of atom (each element) emits a few characteristic frequencies of x-rays, which differ from one atom to the next. The lowest x-ray frequency emitted by each element is found to increase with increasing position in the periodic table.
Most amazingly, there is an unexpected relationship between the frequency and the relative mass of each atom. Let's rank order the elements by atomic mass, and assign an integer to each according to its ranking in order by mass. In the Periodic Table, this rank order number also corresponds to the element's position in the Periodic Table. For example, Hydrogen is assigned 1, Helium is assigned 2, etc. If we now plot the lowest frequency versus the position number in the periodic table, we find that the frequency increases directly as a simple function of the ranking number. This is shown in Figure 4.2, where we have plotted the square root of the x-ray frequency as a function of the ranking number. After a single correction, there is a simple straight-line relationship between these numbers. (The single correction is that the rankings of Argon and Potassium must be reversed. These elements have very similar atomic masses. Although Argon atoms are slightly more massive than Potassium atoms, the Periodic Law requires that we place Argon before Potassium, since Argon is a member of the inert gas group and Potassium is a member of the alkali metal group. By switching their order to correspond to the Periodic Table, we can maintain the beautiful relationship shown in Figure 4.2.)

Figure 4.2: X-ray Frequencies Versus Atomic Number
Why is this simple relationship a surprise? The integer ranking of an element by mass would not seem to be a physical property. We simply assigned these numbers in a listing of the elements which we constructed. However, we have discovered that there is a simple quantitative relationship between a real physical quantity (the x-ray frequency) and the ranking number we assigned. Moreover, there are no "breaks" in the straight line shown in Figure 4.2, meaning that all of the elements in our mass list must be accounted for. Both observations reveal that the ranking number of each atom must also be a real physical quantity itself, directly related to a structural property of each atom. We now call the ranking number the atomic number, since it is a number which uniquely characterizes each atom.
Furthermore, we know that each atom must possess an integer number of positive charges. Since the x-ray data demonstrates a physical property, the atomic number, which is also an integer, the simplest conclusion is that the atomic number from the x-ray data is the number of positive charges in the nucleus. Since each atom is neutral, the atomic number must also equal the number of electrons in a neutral atom.
We now know a great deal about the structure of an atom. We know that the atom has a nuclear structure, we know that the positive charges and mass of the atom are concentrated in the nucleus, and we know how many protons and electrons each atom has. However, we do not yet know anything about the positioning and movement of the electrons in the vast space surrounding the nucleus.
Observation 3: Ionization energies of the atoms
Each electron must move about the nucleus in an electrical field generated by the positive charge of the nucleus and the negative charges of the other electrons. Coulomb's law determines the potential energy of attraction of each electron to the nucleus:
\[V \left( r \right) = \frac{\left( \left( Z \right) e \right) \left( -e \right)}{r}\]
where \(\left( Z \right) e\) is the charge on the nucleus with atomic number \(Z\), \(-e\) is the charge on the electron, and \(r\) is the distance from the electron to the nucleus. The potential energy of the electron in an atom in negative. This is because we take the potential energy of the electron when removed to great distance from the atom (very large \(r\)) to be zero, since the electron and the nucleus do not interact at large distance. In order to remove an electron from an atom, we have to raise the potential energy from its negative value to zero. According to Coulomb's law, we expect electrons closer to the nucleus to have a lower potential energy and thus to require more energy to remove from the atom.
We can directly measure how much energy is required to remove an electron from an atom. Without concerning ourselves with how this measurement is made, we simply measure the minimum amount of energy required to carry out the following "ionization reaction":
\[\ce{A} \left( g \right) \rightarrow \ce{A^+} \left( g \right) + \ce{e^-} \left( g \right)\]
Here, \(\ce{A}\) is an atom in the gas phase, and \(\ce{A^+}\) is the same atom with one electron \(\ce{e^-}\) removed and is thus an ion. The minimum energy required to perform the ionization is called the ionization energy. The values of the ionization energy for each atom in Groups I through VIII of the periodic table are shown as a function of the atomic number in Figure 4.3.

Figure 4.3: Ionization Energy Versus Atomic Number
This figure is very reminiscent of the Periodic Law, which states that chemical and physical properties of the elements are periodic functions of the atomic number. Notice that the elements with the largest ionization energies (in other words, the most tightly bound electrons) are the inert gases. By contrast, the alkali metals are the elements with the smallest ionization energies. In a single period of the periodic table, between each alkali metal atom and the next inert gas atom, the ionization energy rises fairly steadily, falling dramatically from the inert gas to the following alkali metal at the start of the next period.
We need a model which accounts for these variations in the ionization energy. A reasonable assumption from Coulomb's law is that these variations are due to variations in the nuclear charge (atomic number) and in the distance of the electrons from the nucleus. To begin, we can make a very crude approximation that the ionization energy is just the negative of this attractive potential energy given by Coulomb's law. This is crude because we have ignored the kinetic energy and because each electron may not have fixed value of \(r\).
Nevertheless, this approximation gives a way to analyze Figure 4.3. For example, from Coulomb's law it seems to make sense that the ionization energy should increase with increasing atomic number. It is easier to remove an electron from Lithium than from Neon because the nuclear charge in Lithium is much smaller than in Neon. But this cannot be the whole picture, because this argument would imply that Sodium atoms should have greater ionization energy than Neon atoms, when in fact Sodium atoms have a very much lower ionization energy. Similarly, although the ionization energy rises as we go from Sodium to Argon, the ionization energy of Argon is still less than that of Neon, even though the nuclear charge in an Argon atom is much greater than the nuclear charge in a Neon atom. What have we omitted from our analysis?
The answer is that we must consider also the distance of the electrons from th e nucleus. Since it requires much less energy to ionize a Sodium atom than to ionize a Neon atom even though Sodium's nuclear charge is greater, it must be that the electron which remove from a Sodium atom is much farther from the nucleus than the electron in the Neon atom. We can make the same comparison of the electrons removed during ionization of Neon and Argon atoms: the Argon electron must be farther from the nucleus than the Neon electron.
On the other hand, since the ionization energy fairly smoothly increases as we move from Lithium to Neon in the second period of elements, this reveals that the electrons are increasingly attracted to the nucleus for greater nuclear charge and suggests that the electrons' distance from the nucleus might not be varying too greatly over the course of a single period of the table.
If we follow this reasoning, we can even estimate how far an electron might typically be from the nucleus by using our crude approximation that the ionization energy is equal to the negative of the Coulomb potential and solving for \(r\) for each atom. This gives an estimate of distance of the electron from the nucleus:
\[r_\text{shell} = -\frac{\left( \left( Z \right) e \right) \left( -e \right)}{\text{ionization energy}}\]
Values of \(r_\text{shell}\) calculated in this way are shown for the first 20 elements in Figure 4.4. Also shown for comparison is the ionization energy for these elements. Notice that the approximate distance of the electrons from the nucleus increases in steps exactly coinciding with the increases and dips in the ionization energy.

Figure 4.4: Ionization energy and \(r_\text{shell}\) versus Atomic Number
Although these distances we have calculated do not have a precise physical meaning, Figure 4.4 suggests a significant conclusion. The electrons in the elements are arranged into "shells" of increasingly greater distance from the nucleus. Hydrogen and Helium, with one and two electrons, have ionization energies consistent with electrons at similar and close distance from the nucleus. Then the second row elements lithium through neon have virtually identical sizes, though larger than that for the first two elements. The third row elements, sodium through argon, have an approximate electron-nuclear distance which fluctuates a bit but is consistently larger than the second row elements.
Because the sizes of the atoms appear to grow in steps which correspond exactly to the periods of the Periodic table, it seems that the electrons in the atoms are grouped into sets which are differing distances away from the nucleus. The first two electrons, as in Helium, are close to the nucleus, whereas additional electrons, as in Lithium to Neon, are farther from the nucleus than the first two. This suggests that, for atoms Lithium to Neon, the first two electrons are in an inner "shell", and the remaining electrons are in an outer "shell".
We can refine this shell model for the electrons in an atom with further analysis of ionization energies. We can remove any number of electrons in sequence, forming ions with greater charge. We have been examining the first ionization energy, \(IE_1\), but each successively removed electron has successively greater ionization energy:
First ionization energy \(IE_1\):
\[\ce{A} \left( g \right) \rightarrow \ce{A+} \left( g \right) + \ce{e^-} \left( g \right)\]
Second ionization energy \(IE_2\):
\[\ce{A^+} \left( g \right) \rightarrow \ce{A^{2+}} \left( g \right) + \ce{e^-} \left( g \right)\]
Third ionization energy \(IE_3\):
\[\ce{A^{2+}} \left( g \right) \rightarrow \ce{A^{3+}} \left( g \right) + \ce{e^-} \left( g \right)\]
The sequential ionization energies for the elements in the second row of the periodic table are shown below.
Table 4.1: Successive Ionization Energies \(\text{kJ/mol}\)
| \(\ce{Na}\) | \(\ce{Mg}\) | \(\ce{Al}\) | \(\ce{Si}\) | \(\ce{P}\) | \(\ce{S}\) | \(\ce{Cl}\) | \(\ce{Ar}\) | |
|---|---|---|---|---|---|---|---|---|
| \(IE_1\) | 496 | 738 | 578 | 787 | 1012 | 1000 | 1251 | 1520 |
| \(IE_2\) | 4562 | 1451 | 1817 | 1577 | 1903 | 2251 | 2297 | 2665 |
| \(IE_3\) | 6912 | 7733 | 2745 | 3231 | 2912 | 3361 | 3822 | 3931 |
| \(IE_4\) | 9543 | 10540 | 11575 | 4356 | 4956 | 4564 | 5158 | 5770 |
| \(IE_5\) | 13353 | 13630 | 14830 | 16091 | 6273 | 7013 | 6542 | 7238 |
| \(IE_6\) | 16610 | 17995 | 18376 | 19784 | 22233 | 8495 | 9458 | 8781 |
| \(IE_7\) | 20114 | 21703 | 23293 | 23783 | 25397 | 27106 | 11020 | 11995 |
Note that the second ionization energy is always greater than the first, and the third is always greater than the second, etc. This makes sense, since an electron should be more strongly attracted to a positively charged atom than to a neutral atom.
However, the data in the table show a surprising feature. In most cases, the ionization energy increases a fairly large amount for successive ionizations. But for each atom, there is one much larger increase in ionization in the sequence. In \(\ce{Na}\) for example, \(IE_2\) is nearly 10 times greater than \(IE_1\). Similarly, \(IE_3\) is five times greater than \(IE_2\) for \(\ce{Mg}\), although \(IE_2\) is less than twice \(IE_1\). The data for \(\ce{Na}\) through \(\ce{S}\) all show a single large step in addition to the smaller increases in ionization energy.
Looking closely and counting electrons, we see that this unusually large increase always occurs for the ionization where we have already removed all of the outer shell electrons and are now removing an electron from the inner shell. This occurs uniformly across the second row elements, indicating that our shell model is in fact a very accurate predictor of the higher ionization energies. We can now tell how many electrons there are in the outer shell of each atom: it is equal to the number of electrons since the last inert gas.
We can conclude that an inner shell is "filled" once we have the number of electrons equal to the number in an inert gas atom. The subsequent electrons are added to a new outer shell. This is commonly referred to as the valence shell of the atom.
However, we do not know why only a limited number of electrons can reside in each shell. There is no obvious reason at this point why all the electrons in an atom do not reside in the shell closest to the nucleus. Similarly, there is no reason given for why the number of electrons in an inert gas atom exactly fills the outer shell, without room for even a single additional electron. These questions must be addressed further.
Review and Discussion Questions
Explain how the scattering of \(\alpha\) particles from gold foil reveals that an atom contains a massive, positively charged nucleus whose size is much smaller than that of the atom.
Explain the significance of the relationship between the frequency of x-ray emission from each atom and the atomic ranking of that atom in the periodic table.
Provide experimental evidence which reveals that the electrons in an atom are grouped into a valence shell and inner shell electrons.
State and explain the evidence which reveals that the outer shell of each inert gas atom is full.
Why does the ionization energy for each successive ionization increase for every atom? Why is the increase from \(IE_4\) to \(IE_5\) in \(\ce{Si}\) much larger than any of the other increases for \(\ce{Si}\)?
Contributors and Attributions
John S. Hutchinson (Rice University; Chemistry)

