5.E: Advanced Theories of Covalent Bonding (Exercises)
- Page ID
- 78578
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)8.1: Valence Bond Theory
Chapter Exercises
- Explain how σ and π bonds are similar and how they are different.
- Draw a curve that describes the energy of a system with H and Cl atoms at varying distances. Then, find the minimum energy of this curve two ways.
- Use the bond energy found in Table 8.2.1 to calculate the energy for one single HCl bond (Hint: How many bonds are in a mole?)
- Use the enthalpy of reaction and the bond energies for \(H_2\) and \(Cl_2\) to solve for the energy of one mole of HCl bonds. \[H_{2(g)}+Cl_{2(g)} \rightleftharpoons 2HCl_{(g)} \;\;\; ΔH^∘_{rxn}=−184.7\; kJ/mol\]
- Explain why bonds occur at specific average bond distances instead of the atoms approaching each other infinitely close.
- Use valence bond theory to explain the bonding in F2, HF, and ClBr. Sketch the overlap of the atomic orbitals involved in the bonds.
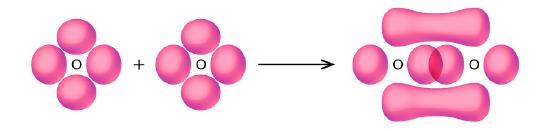
- Use valence bond theory to explain the bonding in O2. Sketch the overlap of the atomic orbitals involved in the bonds in O2.
- How many σ and π bonds are present in the molecule HCN?
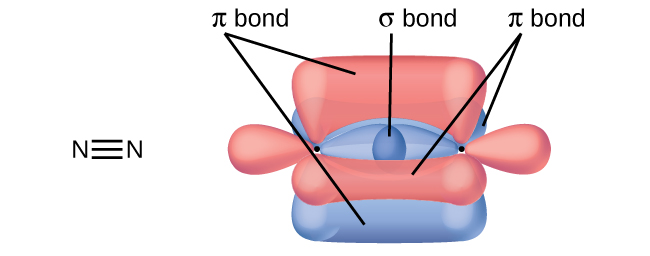
- A friend tells you N2 has three π bonds due to overlap of the three p-orbitals on each N atom. Do you agree?
- Draw the Lewis structures for CO2 and CO, and predict the number of σ and π bonds for each molecule.
- CO2
- CO
Solutions
1. Similarities: Both types of bonds result from overlap of atomic orbitals on adjacent atoms and contain a maximum of two electrons. Differences: σ bonds are stronger and result from end-to-end overlap and all single bonds are σ bonds; π bonds between the same two atoms are weaker because they result from side-by-side overlap, and multiple bonds contain one or more π bonds (in addition to a σ bond).
2
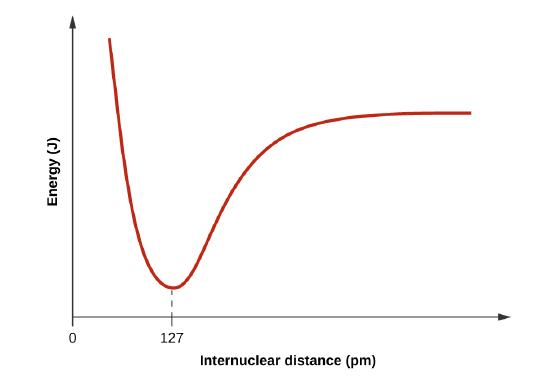
When H and Cl are separate (the x axis) the energy is at a particular value. As they approach, it decreases to a minimum at 127 pm (the bond distance), and then it increases sharply as you get closer.
- (a) H–Cl431 kJ/mol 427kJmol×mol6.022×1023bonds×1000 JkJ=7.09×10−19
- (b) We know Hess’s law related to bond energies: ΔH°=ƩΔH∘BDE(broken)−ƩΔH∘BDE(formed) We are given the enthalpy of reaction
\[−184.7 kJ/mol=(ΔH∘BDE(H–H)+ΔH∘BDE(Cl–Cl))−(2ΔH∘BDE(H–Cl))\]
\[H–H is 436 kJ/mol and Cl–Cl is 243\]
\[–184.7 kJ/mol = (436 + 243) – 2x = 679 – 2x\]
\[2x = 863.7 kJ/mol\]
\[x = 432\; kJ/mol\]
This is very close to the value from part (a).
3. The specific average bond distance is the distance with the lowest energy. At distances less than the bond distance, the positive charges on the two nuclei repel each other, and the overall energy increases.
4. The single bond present in each molecule results from overlap of the relevant orbitals: F 2p orbitals in F2, the H 1s and F 2p orbitals in HF, and the Cl 3p orbital and Br 4p orbital in ClBr.
5. Bonding: One σ bond and one π bond. The s orbitals are filled and do not overlap. The p orbitals overlap along the axis to form a σ bond and side by side to form the π bond.
6. \(\ce{H–C≡N}\) has two σ (H–C and C–N) and two π (making the CN triple bond).

7. No, two of the p orbitals (one on each N) will be oriented end-to-end and will form a σ bond.
8. (a) 2 σ 2 π;
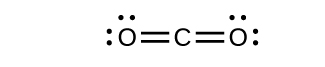
(b) 1 σ 2 π;
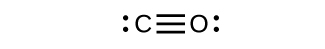
8.2: Hybrid Atomic Orbitals
Chemistry End of Chapter Exercises
Why is the concept of hybridization required in valence bond theory?
Hybridization is introduced to explain the geometry of bonding orbitals in valance bond theory.
Give the shape that describes each hybrid orbital set:
(a) sp2
(b) sp3d
(c) sp
(d) sp3d2
Explain why a carbon atom cannot form five bonds using sp3d hybrid orbitals.
There are no d orbitals in the valence shell of carbon.
What is the hybridization of the central atom in each of the following?
(a) BeH2
(b) SF6
(c) \(\ce{PO4^3-}\)
(d) PCl5
A molecule with the formula AB3 could have one of four different shapes. Give the shape and the hybridization of the central A atom for each.
trigonal planar, sp2; trigonal pyramidal (one lone pair on A) sp3; T-shaped (two lone pairs on A sp3d, or (three lone pairs on A) sp3d2
Methionine, CH3SCH2CH2CH(NH2)CO2H, is an amino acid found in proteins. Draw a Lewis structure of this compound. What is the hybridization type of each carbon, oxygen, the nitrogen, and the sulfur?

Sulfuric acid is manufactured by a series of reactions represented by the following equations:
\(\ce{S8}(s)+\ce{8O2}(g)⟶\ce{8SO2}(g)\)
\(\ce{2SO2}(g)+\ce{O2}(g)⟶\ce{2SO3}(g)\)
\(\ce{SO3}(g)+\ce{H2O}(l)⟶\ce{H2SO4}(l)\)
Draw a Lewis structure, predict the molecular geometry by VSEPR, and determine the hybridization of sulfur for the following:
(a) circular S8 molecule
(b) SO2 molecule
(c) SO3 molecule
(d) H2SO4 molecule (the hydrogen atoms are bonded to oxygen atoms)
(a) Each S has a bent (109°) geometry, sp3

(b) Bent (120°), sp2

(c) Trigonal planar, sp2

(d) Tetrahedral, sp3

Two important industrial chemicals, ethene, C2H4, and propene, C3H6, are produced by the steam (or thermal) cracking process:
\(\ce{2C3H8}(g)⟶\ce{C2H4}(g)+\ce{C3H6}(g)+\ce{CH4}(g)+\ce{H2}(g)\)For each of the four carbon compounds, do the following:
(a) Draw a Lewis structure.
(b) Predict the geometry about the carbon atom.
(c) Determine the hybridization of each type of carbon atom.
For many years after they were discovered, it was believed that the noble gases could not form compounds. Now we know that belief to be incorrect. A mixture of xenon and fluorine gases, confined in a quartz bulb and placed on a windowsill, is found to slowly produce a white solid. Analysis of the compound indicates that it contains 77.55% Xe and 22.45% F by mass.
(a) What is the formula of the compound?
(b) Write a Lewis structure for the compound.
(c) Predict the shape of the molecules of the compound.
(d) What hybridization is consistent with the shape you predicted?
(a) XeF2
(b)

(c) linear (d) sp3d
Consider nitrous acid, HNO2 (HONO).
(a) Write a Lewis structure.
(b) What are the electron pair and molecular geometries of the internal oxygen and nitrogen atoms in the HNO2 molecule?
(c) What is the hybridization on the internal oxygen and nitrogen atoms in HNO2?
Strike-anywhere matches contain a layer of KClO3 and a layer of P4S3. The heat produced by the friction of striking the match causes these two compounds to react vigorously, which sets fire to the wooden stem of the match. KClO3 contains the \(\ce{ClO3-}\) ion. P4S3 is an unusual molecule with the skeletal structure.

(a) Write Lewis structures for P4S3 and the \(\ce{ClO3-}\) ion.
(b) Describe the geometry about the P atoms, the S atom, and the Cl atom in these species.
(c) Assign a hybridization to the P atoms, the S atom, and the Cl atom in these species.
(d) Determine the oxidation states and formal charge of the atoms in P4S3 and the \(\ce{ClO3-}\) ion.
(a)

(b) P atoms, trigonal pyramidal; S atoms, bent, with two lone pairs; Cl atoms, trigonal pyramidal; (c) Hybridization about P, S, and Cl is, in all cases, sp3; (d) Oxidation states P +1, S \(−1\dfrac{1}{3}\), Cl +5, O –2. Formal charges: P 0; S 0; Cl +2: O –1
Identify the hybridization of each carbon atom in the following molecule. (The arrangement of atoms is given; you need to determine how many bonds connect each pair of atoms.)

Write Lewis structures for NF3 and PF5. On the basis of hybrid orbitals, explain the fact that NF3, PF3, and PF5 are stable molecules, but NF5 does not exist.

Phosphorus and nitrogen can form sp3 hybrids to form three bonds and hold one lone pair in PF3 and NF3, respectively. However, nitrogen has no valence d orbitals, so it cannot form a set of sp3d hybrid orbitals to bind five fluorine atoms in NF5. Phosphorus has d orbitals and can bind five fluorine atoms with sp3d hybrid orbitals in PF5.
In addition to NF3, two other fluoro derivatives of nitrogen are known: N2F4 and N2F2. What shapes do you predict for these two molecules? What is the hybridization for the nitrogen in each molecule?
8.3: Multiple Bonds
Chemistry End of Chapter Exercises
The bond energy of a C–C single bond averages 347 kJ mol−1; that of a C≡C triple bond averages 839 kJ mol−1. Explain why the triple bond is not three times as strong as a single bond.
A triple bond consists of one σ bond and two π bonds. A σ bond is stronger than a π bond due to greater overlap.
For the carbonate ion, \(\ce{CO3^2-}\), draw all of the resonance structures. Identify which orbitals overlap to create each bond.
A useful solvent that will dissolve salts as well as organic compounds is the compound acetonitrile, H3CCN. It is present in paint strippers.
(a) Write the Lewis structure for acetonitrile, and indicate the direction of the dipole moment in the molecule.
(b) Identify the hybrid orbitals used by the carbon atoms in the molecule to form σ bonds.
(c) Describe the atomic orbitals that form the π bonds in the molecule. Note that it is not necessary to hybridize the nitrogen atom.
(a)

(b) The terminal carbon atom uses sp3 hybrid orbitals, while the central carbon atom is sp hybridized. (c) Each of the two π bonds is formed by overlap of a 2p orbital on carbon and a nitrogen 2p orbital.
For the molecule allene, \(\mathrm{H_2C=C=CH_2}\), give the hybridization of each carbon atom. Will the hydrogen atoms be in the same plane or perpendicular planes?
Identify the hybridization of the central atom in each of the following molecules and ions that contain multiple bonds:
(a) ClNO (N is the central atom)
(b) CS2
(c) Cl2CO (C is the central atom)
(d) Cl2SO (S is the central atom)
(e) SO2F2 (S is the central atom)
(f) XeO2F2 (Xe is the central atom)
(g) \(\ce{ClOF2+}\) (Cl is the central atom)
(a) sp2; (b) sp; (c) sp2; (d) sp3; (e) sp3; (f) sp3d; (g) sp3
Describe the molecular geometry and hybridization of the N, P, or S atoms in each of the following compounds.
(a) H3PO4, phosphoric acid, used in cola soft drinks
(b) NH4NO3, ammonium nitrate, a fertilizer and explosive
(c) S2Cl2, disulfur dichloride, used in vulcanizing rubber
(d) K4[O3POPO3], potassium pyrophosphate, an ingredient in some toothpastes
For each of the following molecules, indicate the hybridization requested and whether or not the electrons will be delocalized:
(a) ozone (O3) central O hybridization
(b) carbon dioxide (CO2) central C hybridization
(c) nitrogen dioxide (NO2) central N hybridization
(d) phosphate ion (\(\ce{PO4^3-}\)) central P hybridization
(a) sp2, delocalized; (b) sp, localized; (c) sp2, delocalized; (d) sp3, delocalized
For each of the following structures, determine the hybridization requested and whether the electrons will be delocalized:
(a) Hybridization of each carbon

(b) Hybridization of sulfur

(c) All atoms

Draw the orbital diagram for carbon in CO2 showing how many carbon atom electrons are in each orbital.

Each of the four electrons is in a separate orbital and overlaps with an electron on an oxygen atom.
8.4: Molecular Orbital Theory
Chemistry End of Chapter Exercises
Sketch the distribution of electron density in the bonding and antibonding molecular orbitals formed from two s orbitals and from two p orbitals.
How are the following similar, and how do they differ?
(a) σ molecular orbitals and π molecular orbitals
(b) ψ for an atomic orbital and ψ for a molecular orbital
(c) bonding orbitals and antibonding orbitals
(a) Similarities: Both are bonding orbitals that can contain a maximum of two electrons. Differences: σ orbitals are end-to-end combinations of atomic orbitals, whereas π orbitals are formed by side-by-side overlap of orbitals. (b) Similarities: Both are quantum-mechanical constructs that represent the probability of finding the electron about the atom or the molecule. Differences: ψ for an atomic orbital describes the behavior of only one electron at a time based on the atom. For a molecule, ψ represents a mathematical combination of atomic orbitals. (c) Similarities: Both are orbitals that can contain two electrons. Differences: Bonding orbitals result in holding two or more atoms together. Antibonding orbitals have the effect of destabilizing any bonding that has occurred.
If molecular orbitals are created by combining five atomic orbitals from atom A and five atomic orbitals from atom B combine, how many molecular orbitals will result?
Can a molecule with an odd number of electrons ever be diamagnetic? Explain why or why not.
An odd number of electrons can never be paired, regardless of the arrangement of the molecular orbitals. It will always be paramagnetic.
Can a molecule with an even number of electrons ever be paramagnetic? Explain why or why not.
Why are bonding molecular orbitals lower in energy than the parent atomic orbitals?
Bonding orbitals have electron density in close proximity to more than one nucleus. The interaction between the bonding positively charged nuclei and negatively charged electrons stabilizes the system.
Calculate the bond order for an ion with this configuration:
Explain why an electron in the bonding molecular orbital in the H2 molecule has a lower energy than an electron in the 1s atomic orbital of either of the separated hydrogen atoms.
The pairing of the two bonding electrons lowers the energy of the system relative to the energy of the nonbonded electrons.
Predict the valence electron molecular orbital configurations for the following, and state whether they will be stable or unstable ions.
(a) \(\ce{Na2^2+}\)
(b) \(\ce{Mg2^2+}\)
(c) \(\ce{Al2^2+}\)
(d) \(\ce{Si2^2+}\)
(e) \(\ce{P2^2+}\)
(f) \(\ce{S2^2+}\)
(g) \(\ce{F2^2+}\)
(h) \(\ce{Ar2^2+}\)
Determine the bond order of each member of the following groups, and determine which member of each group is predicted by the molecular orbital model to have the strongest bond.
(a) H2, \(\ce{H2+}\), \(\ce{H2-}\)
(b) O2, \(\ce{O2^2+}\), \(\ce{O2^2-}\)
(c) Li2, \(\ce{Be2+}\), Be2
(d) F2, \(\ce{F2+}\), \(\ce{F2-}\)
(e) N2, \(\ce{N2+}\), \(\ce{N2-}\)
(a) H2 bond order = 1, \(\ce{H2+}\) bond order = 0.5, \(\ce{H2-}\) bond order = 0.5, strongest bond is H2; (b) O2 bond order = 2, \(\ce{O2^2+}\) bond order = 3; \(\ce{O2^2-}\) bond order = 1, strongest bond is \(\ce{O2^2+}\); (c) Li2 bond order = 1, \(\ce{Be2+}\) bond order = 0.5, Be2 bond order = 0, strongest bond is \(\ce{Li2}\);(d) F2 bond order = 1, \(\ce{F2+}\) bond order = 1.5, \(\ce{F2-}\) bond order = 0.5, strongest bond is \(\ce{F2+}\); (e) N2 bond order = 3, \(\ce{N2+}\) bond order = 2.5, \(\ce{N2-}\) bond order = 2.5, strongest bond is N2
For the first ionization energy for an N2 molecule, what molecular orbital is the electron removed from?
Compare the atomic and molecular orbital diagrams to identify the member of each of the following pairs that has the highest first ionization energy (the most tightly bound electron) in the gas phase:
(a) H and H2
(b) N and N2
(c) O and O2
(d) C and C2
(e) B and B2
(a) H2; (b) N2; (c) O; (d) C2; (e) B2
Which of the period 2 homonuclear diatomic molecules are predicted to be paramagnetic?
A friend tells you that the 2s orbital for fluorine starts off at a much lower energy than the 2s orbital for lithium, so the resulting σ2s molecular orbital in F2 is more stable than in Li2. Do you agree?
Yes, fluorine is a smaller atom than Li, so atoms in the 2s orbital are closer to the nucleus and more stable.
True or false: Boron contains 2s22p1 valence electrons, so only one p orbital is needed to form molecular orbitals.
What charge would be needed on F2 to generate an ion with a bond order of 2?
2+
Predict whether the MO diagram for S2 would show s-p mixing or not.
Explain why \(\ce{N2^2+}\) is diamagnetic, while \(\ce{O2^4+}\), which has the same number of valence electrons, is paramagnetic.
N2 has s-p mixing, so the π orbitals are the last filled in \(\ce{N2^2+}\). O2 does not have s-p mixing, so the σp orbital fills before the π orbitals.
Using the MO diagrams, predict the bond order for the stronger bond in each pair:
(a) B2 or \(\ce{B2+}\)
(b) F2 or \(\ce{F2+}\)
(c) O2 or \(\ce{O2^2+}\)
(d) \(\ce{C2+}\) or \(\ce{C2-}\)


