4.3: Classifying Chemical Reactions
- Page ID
- 38155
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Define three common types of chemical reactions (precipitation, acid-base, and oxidation-reduction)
- Classify chemical reactions as one of these three types given appropriate descriptions or chemical equations
- Identify common acids and bases
- Predict the solubility of common inorganic compounds by using solubility rules
- Compute the oxidation states for elements in compounds
Humans interact with one another in various and complex ways, and we classify these interactions according to common patterns of behavior. When two humans exchange information, we say they are communicating. When they exchange blows with their fists or feet, we say they are fighting. Faced with a wide range of varied interactions between chemical substances, scientists have likewise found it convenient (or even necessary) to classify chemical interactions by identifying common patterns of reactivity. This module will provide an introduction to three of the most prevalent types of chemical reactions: precipitation, acid-base, and oxidation-reduction.
Precipitation Reactions and Solubility Rules
A precipitation reaction is one in which dissolved substances react to form one (or more) solid products. Many reactions of this type involve the exchange of ions between ionic compounds in aqueous solution and are sometimes referred to as double displacement, double replacement, or metathesis reactions. These reactions are common in nature and are responsible for the formation of coral reefs in ocean waters and kidney stones in animals. They are used widely in industry for production of a number of commodity and specialty chemicals. Precipitation reactions also play a central role in many chemical analysis techniques, including spot tests used to identify metal ions and gravimetric methods for determining the composition of matter (see the last module of this chapter).
The extent to which a substance may be dissolved in water, or any solvent, is quantitatively expressed as its solubility, defined as the maximum concentration of a substance that can be achieved under specified conditions. Substances with relatively large solubilities are said to be soluble. A substance will precipitate when solution conditions are such that its concentration exceeds its solubility. Substances with relatively low solubilities are said to be insoluble, and these are the substances that readily precipitate from solution. More information on these important concepts is provided in the text chapter on solutions. For purposes of predicting the identities of solids formed by precipitation reactions, one may simply refer to patterns of solubility that have been observed for many ionic compounds (Table \(\PageIndex{1}\)).
| Soluble compounds contain | Exceptions to these solubility rules include |
|
|
| Insoluble compounds contain | Exceptions to these insolubility rules include |
|
|
A vivid example of precipitation is observed when solutions of potassium iodide and lead nitrate are mixed, resulting in the formation of solid lead iodide:
\[\ce{2KI}(aq)+\ce{Pb(NO3)2}(aq)\rightarrow \ce{PbI2}(s)+\ce{2KNO3}(aq) \nonumber \]
This observation is consistent with the solubility guidelines: The only insoluble compound among all those involved is lead iodide, one of the exceptions to the general solubility of iodide salts.
The net ionic equation representing this reaction is:
\[\ce{Pb^2+}(aq)+\ce{2I-}(aq)\rightarrow \ce{PbI2}(s) \nonumber \]
Lead iodide is a bright yellow solid that was formerly used as an artist’s pigment known as iodine yellow (Figure \(\PageIndex{1}\)). The properties of pure PbI2 crystals make them useful for fabrication of X-ray and gamma ray detectors.

The solubility guidelines in Table \(\PageIndex{1}\) may be used to predict whether a precipitation reaction will occur when solutions of soluble ionic compounds are mixed together. One merely needs to identify all the ions present in the solution and then consider if possible cation/anion pairing could result in an insoluble compound. For example, mixing solutions of silver nitrate and sodium fluoride will yield a solution containing Ag+, \(\ce{NO3-}\), Na+, and F− ions. Aside from the two ionic compounds originally present in the solutions, AgNO3 and NaF, two additional ionic compounds may be derived from this collection of ions: NaNO3 and AgF. The solubility guidelines indicate all nitrate salts are soluble but that AgF is one of the exceptions to the general solubility of fluoride salts. A precipitation reaction, therefore, is predicted to occur, as described by the following equations:
\[\ce{NaF}(aq)+\ce{AgNO3}(aq)\rightarrow \ce{AgF}(s)+\ce{NaNO3}(aq)\hspace{20px}\ce{(molecular)} \nonumber \]
\[\ce{Ag+}(aq)+\ce{F-}(aq)\rightarrow \ce{AgF}(s)\hspace{20px}\ce{(net\: ionic)} \nonumber \]
Predict the result of mixing reasonably concentrated solutions of the following ionic compounds. If precipitation is expected, write a balanced net ionic equation for the reaction.
- potassium sulfate and barium nitrate
- lithium chloride and silver acetate
- lead nitrate and ammonium carbonate
Solution
(a) The two possible products for this combination are KNO3 and BaSO4. The solubility guidelines indicate BaSO4 is insoluble, and so a precipitation reaction is expected. The net ionic equation for this reaction, derived in the manner detailed in the previous module, is
\[\ce{Ba^2+}(aq)+\ce{SO4^2-}(aq)\rightarrow \ce{BaSO4}(s) \nonumber \]
(b) The two possible products for this combination are LiC2H3O2 and AgCl. The solubility guidelines indicate AgCl is insoluble, and so a precipitation reaction is expected. The net ionic equation for this reaction, derived in the manner detailed in the previous module, is
\[\ce{Ag+}(aq)+\ce{Cl-}(aq)\rightarrow \ce{AgCl}(s) \nonumber \]
(c) The two possible products for this combination are PbCO3 and NH4NO3. The solubility guidelines indicate PbCO3 is insoluble, and so a precipitation reaction is expected. The net ionic equation for this reaction, derived in the manner detailed in the previous module, is
\[\ce{Pb^2+}(aq)+\ce{CO3^2-}(aq)\rightarrow \ce{PbCO3}(s) \nonumber \]
Which solution could be used to precipitate the barium ion, Ba2+, in a water sample: sodium chloride, sodium hydroxide, or sodium sulfate? What is the formula for the expected precipitate?
- Answer
-
sodium sulfate, BaSO4
Acid-Base Reactions
An acid-base reaction is one in which a hydrogen ion, H+, is transferred from one chemical species to another. Such reactions are of central importance to numerous natural and technological processes, ranging from the chemical transformations that take place within cells and the lakes and oceans, to the industrial-scale production of fertilizers, pharmaceuticals, and other substances essential to society. The subject of acid-base chemistry, therefore, is worthy of thorough discussion, and a full chapter is devoted to this topic later in the text.
For purposes of this brief introduction, we will consider only the more common types of acid-base reactions that take place in aqueous solutions. In this context, an acid is a substance that will dissolve in water to yield hydronium ions, H3O+. As an example, consider the equation shown here:
\[\ce{HCl}(aq)+\ce{H2O}(aq)\rightarrow \ce{Cl-}(aq)+\ce{H3O+}(aq) \nonumber \]
The process represented by this equation confirms that hydrogen chloride is an acid. When dissolved in water, H3O+ ions are produced by a chemical reaction in which H+ ions are transferred from HCl molecules to H2O molecules (Figure \(\PageIndex{2}\)).
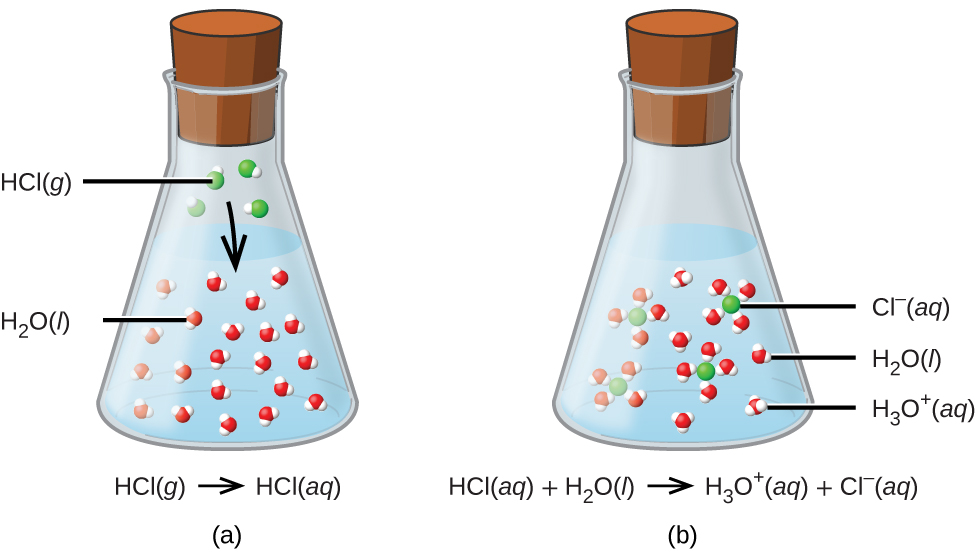
The nature of HCl is such that its reaction with water as just described is essentially 100% efficient: Virtually every HCl molecule that dissolves in water will undergo this reaction. Acids that completely react in this fashion are called strong acids, and HCl is one among just a handful of common acid compounds that are classified as strong (Table \(\PageIndex{1}\)). A far greater number of compounds behave as weak acids and only partially react with water, leaving a large majority of dissolved molecules in their original form and generating a relatively small amount of hydronium ions. Weak acids are commonly encountered in nature, being the substances partly responsible for the tangy taste of citrus fruits, the stinging sensation of insect bites, and the unpleasant smells associated with body odor. A familiar example of a weak acid is acetic acid, the main ingredient in food vinegars:
\[\ce{CH3CO2H}(aq)+\ce{H2O}(l)\rightleftharpoons \ce{CH3CO2-}(aq)+\ce{H3O+}(aq) \nonumber \]
When dissolved in water under typical conditions, only about 1% of acetic acid molecules are present in the ionized form, \(\ce{CH3CO2-}\) (Figure \(\PageIndex{3}\)). (The use of a double-arrow in the equation above denotes the partial reaction aspect of this process, a concept addressed fully in the chapters on chemical equilibrium.)
| Compound Formula | Name in Aqueous Solution |
|---|---|
| HBr | hydrobromic acid |
| HCl | hydrochloric acid |
| HI | hydroiodic acid |
| HNO3 | nitric acid |
| HClO4 | perchloric acid |
| H2SO4 | sulfuric acid |
A base is a substance that will dissolve in water to yield hydroxide ions, OH−. The most common bases are ionic compounds composed of alkali or alkaline earth metal cations (groups 1 and 2) combined with the hydroxide ion—for example, NaOH and Ca(OH)2. When these compounds dissolve in water, hydroxide ions are released directly into the solution. For example, KOH and Ba(OH)2 dissolve in water and dissociate completely to produce cations (K+ and Ba2+, respectively) and hydroxide ions, OH−. These bases, along with other hydroxides that completely dissociate in water, are considered strong bases.
Consider as an example the dissolution of lye (sodium hydroxide) in water:
\[\ce{NaOH}(s)\rightarrow \ce{Na+}(aq)+\ce{OH-}(aq) \nonumber \]
This equation confirms that sodium hydroxide is a base. When dissolved in water, NaOH dissociates to yield Na+ and OH− ions. This is also true for any other ionic compound containing hydroxide ions. Since the dissociation process is essentially complete when ionic compounds dissolve in water under typical conditions, NaOH and other ionic hydroxides are all classified as strong bases.
Unlike ionic hydroxides, some compounds produce hydroxide ions when dissolved by chemically reacting with water molecules. In all cases, these compounds react only partially and so are classified as weak bases. These types of compounds are also abundant in nature and important commodities in various technologies. For example, global production of the weak base ammonia is typically well over 100 metric tons annually, being widely used as an agricultural fertilizer, a raw material for chemical synthesis of other compounds, and an active ingredient in household cleaners (Figure \(\PageIndex{4}\)). When dissolved in water, ammonia reacts partially to yield hydroxide ions, as shown here:
\[\ce{NH3}(aq)+\ce{H2O}(l)\rightleftharpoons \ce{NH4+}(aq)+\ce{OH-}(aq) \nonumber \]
This is, by definition, an acid-base reaction, in this case involving the transfer of H+ ions from water molecules to ammonia molecules. Under typical conditions, only about 1% of the dissolved ammonia is present as \(\ce{NH4+}\) ions.

The chemical reactions described in which acids and bases dissolved in water produce hydronium and hydroxide ions, respectively, are, by definition, acid-base reactions. In these reactions, water serves as both a solvent and a reactant. A neutralization reaction is a specific type of acid-base reaction in which the reactants are an acid and a base, the products are often a salt and water, and neither reactant is the water itself:
\[\mathrm{acid+base\rightarrow salt+water} \nonumber \]
To illustrate a neutralization reaction, consider what happens when a typical antacid such as milk of magnesia (an aqueous suspension of solid Mg(OH)2) is ingested to ease symptoms associated with excess stomach acid (HCl):
\[\ce{Mg(OH)2}(s)+\ce{2HCl}(aq)\rightarrow \ce{MgCl2}(aq)+\ce{2H2O}(l). \nonumber \]
Note that in addition to water, this reaction produces a salt, magnesium chloride.
Write balanced chemical equations for the acid-base reactions described here:
- the weak acid hydrogen hypochlorite reacts with water
- a solution of barium hydroxide is neutralized with a solution of nitric acid
Solution
(a) The two reactants are provided, HOCl and H2O. Since the substance is reported to be an acid, its reaction with water will involve the transfer of H+ from HOCl to H2O to generate hydronium ions, H3O+ and hypochlorite ions, OCl−.
\[\ce{HOCl}(aq)+\ce{H2O}(l)\rightleftharpoons \ce{OCl-}(aq)+\ce{H3O+}(aq) \nonumber \]
A double-arrow is appropriate in this equation because it indicates the HOCl is a weak acid that has not reacted completely.
(b) The two reactants are provided, Ba(OH)2 and HNO3. Since this is a neutralization reaction, the two products will be water and a salt composed of the cation of the ionic hydroxide (Ba2+) and the anion generated when the acid transfers its hydrogen ion \(\ce{(NO3- )}\).
\[\ce{Ba(OH)2}(aq)+\ce{2HNO3}(aq)\rightarrow \ce{Ba(NO3)2}(aq)+\ce{2H2O}(l) \nonumber \]
Write the net ionic equation representing the neutralization of any strong acid with an ionic hydroxide. (Hint: Consider the ions produced when a strong acid is dissolved in water.)
- Answer
-
\[\ce{H3O+}(aq)+\ce{OH-}(aq)\rightarrow \ce{2H2O}(l) \nonumber \]
Explore the microscopic view of strong and weak acids and bases.
Oxidation-Reduction Reactions
Earth’s atmosphere contains about 20% molecular oxygen, O2, a chemically reactive gas that plays an essential role in the metabolism of aerobic organisms and in many environmental processes that shape the world. The term oxidation was originally used to describe chemical reactions involving O2, but its meaning has evolved to refer to a broad and important reaction class known as oxidation-reduction (redox) reactions. A few examples of such reactions will be used to develop a clear picture of this classification.
Some redox reactions involve the transfer of electrons between reactant species to yield ionic products, such as the reaction between sodium and chlorine to yield sodium chloride:
\[\ce{2Na}(s)+\ce{Cl2}(g)\rightarrow \ce{2NaCl}(s) \nonumber \]
It is helpful to view the process with regard to each individual reactant, that is, to represent the fate of each reactant in the form of an equation called a half-reaction:
\[ \begin{align*} \ce{2Na}(s) &\rightarrow \ce{2Na+}(s)+\ce{2e-} \\[4pt] \ce{Cl2}(g)+\ce{2e-} &\rightarrow \ce{2Cl-}(s) \end{align*} \nonumber \]
These equations show that Na atoms lose electrons while Cl atoms (in the Cl2 molecule) gain electrons, the “s” subscripts for the resulting ions signifying they are present in the form of a solid ionic compound. For redox reactions of this sort, the loss and gain of electrons define the complementary processes that occur:
\(\begin{align}
\textbf{oxidation}&=\textrm{loss of electrons}\\
\textbf{reduction}&=\textrm{gain of electrons}
\end{align}\)
In this reaction, then, sodium is oxidized and chlorine undergoes reduction. Viewed from a more active perspective, sodium functions as a reducing agent (reductant), since it provides electrons to (or reduces) chlorine. Likewise, chlorine functions as an oxidizing agent (oxidant), as it effectively removes electrons from (oxidizes) sodium.
\(\begin{align}
\textbf{reducing agent}&=\textrm{species that is oxidized}\\
\textbf{oxidizing agent}&=\textrm{species that is reduced}
\end{align}\)
Some redox processes, however, do not involve the transfer of electrons. Consider, for example, a reaction similar to the one yielding \(\ce{NaCl}\):
\[\ce{H2}(g)+\ce{Cl2}(g)\rightarrow \ce{2HCl}(g) \nonumber \]
The product of this reaction is a covalent compound, so transfer of electrons in the explicit sense is not involved. To clarify the similarity of this reaction to the previous one and permit an unambiguous definition of redox reactions, a property called oxidation number has been defined. The oxidation number (or oxidation state) of an element in a compound is the charge its atoms would possess if the compound was ionic. The following guidelines are used to assign oxidation numbers to each element in a molecule or ion.
- The oxidation number of an atom in an elemental substance is zero.
- The oxidation number of a monatomic ion is equal to the ion’s charge.
- Oxidation numbers for common nonmetals are usually assigned as follows:
- Hydrogen: +1 when combined with nonmetals, −1 when combined with metals
- Oxygen: −2 in most compounds, sometimes −1 (so-called peroxides, \(\ce{O2^2-}\)), very rarely \(-\dfrac{1}{2}\) (so-called superoxides, \(\ce{O2-}\)), positive values when combined with F (values vary)
- Halogens: −1 for F always, −1 for other halogens except when combined with oxygen or other halogens (positive oxidation numbers in these cases, varying values)
- The sum of oxidation numbers for all atoms in a molecule or polyatomic ion equals the charge on the molecule or ion.
Note: The proper convention for reporting charge is to write the number first, followed by the sign (e.g., 2+), while oxidation number is written with the reversed sequence, sign followed by number (e.g., +2). This convention aims to emphasize the distinction between these two related properties.
Follow the guidelines in this section of the text to assign oxidation numbers to all the elements in the following species:
- H2S
- \(\ce{SO3^2-}\)
- Na2SO4
Solution
(a) According to guideline 1, the oxidation number for H is +1.
Using this oxidation number and the compound’s formula, guideline 4 may then be used to calculate the oxidation number for sulfur:
\(\ce{charge\: on\: H2S}=0=(2\times +1)+(1\times x)\)
\(x=0-(2\times +1)=-2\)
(b) Guideline 3 suggests the oxidation number for oxygen is −2.
Using this oxidation number and the ion’s formula, guideline 4 may then be used to calculate the oxidation number for sulfur:
\(\ce{charge\: on\: SO3^2-}=-2=(3\times -2)+(1\times x)\)
\(x=-2-(3\times -2)=+4\)
(c) For ionic compounds, it’s convenient to assign oxidation numbers for the cation and anion separately.
According to guideline 2, the oxidation number for sodium is +1.
Assuming the usual oxidation number for oxygen (−2 per guideline 3), the oxidation number for sulfur is calculated as directed by guideline 4:
\(x=-2-(4\times -2)=+6\)
Assign oxidation states to the elements whose atoms are underlined in each of the following compounds or ions:
- KNO3
- AlH3
- \(\mathrm{\underline{N}H_4^+}\)
- \(\mathrm{\sideset{ }{_{\large{4}}^{-}}{H_2\underline{P}O}}\)
- Answer a
-
N, +5
- Answer b
-
Al, +3
- Answer c
-
N, −3
- Answer d
-
P, +5
Using the oxidation number concept, an all-inclusive definition of redox reaction has been established. Oxidation-reduction (redox) reactions are those in which one or more elements involved undergo a change in oxidation number. While the vast majority of redox reactions involve changes in oxidation number for two or more elements, a few interesting exceptions to this rule do exist as shown below\). Definitions for the complementary processes of this reaction class are correspondingly revised as shown here:
\[\begin{align}
\textbf{oxidation}&=\textrm{increase in oxidation number}\\
\textbf{reduction}&=\textrm{decrease in oxidation number}
\end{align} \nonumber \]
Returning to the reactions used to introduce this topic, they may now both be identified as redox processes. In the reaction between sodium and chlorine to yield sodium chloride, sodium is oxidized (its oxidation number increases from 0 in Na to +1 in NaCl) and chlorine is reduced (its oxidation number decreases from 0 in Cl2 to −1 in NaCl). In the reaction between molecular hydrogen and chlorine, hydrogen is oxidized (its oxidation number increases from 0 in H2 to +1 in HCl) and chlorine is reduced (its oxidation number decreases from 0 in Cl2 to −1 in HCl).
Several subclasses of redox reactions are recognized, including combustion reactions in which the reductant (also called a fuel) and oxidant (often, but not necessarily, molecular oxygen) react vigorously and produce significant amounts of heat, and often light, in the form of a flame. Solid rocket-fuel reactions such as the one depicted below are combustion processes. A typical propellant reaction in which solid aluminum is oxidized by ammonium perchlorate is represented by this equation:
\[\ce{10Al}(s)+\ce{6NH4ClO4}(s)\rightarrow \ce{4Al2O3}(s)+\ce{2AlCl3}(s)+\ce{12H2O}(g)+\ce{3N2}(g) \nonumber \]
Watch a brief video showing the test firing of a small-scale, prototype, hybrid rocket engine planned for use in the new Space Launch System being developed by NASA. The first engines firing at 3 s (green flame) use a liquid fuel/oxidant mixture, and the second, more powerful engines firing at 4 s (yellow flame) use a solid mixture.
Single-displacement (replacement) reactions are redox reactions in which an ion in solution is displaced (or replaced) via the oxidation of a metallic element. One common example of this type of reaction is the acid oxidation of certain metals:
\[\ce{Zn}(s)+\ce{2HCl}(aq)\rightarrow \ce{ZnCl2}(aq)+\ce{H2}(g) \nonumber \]
Metallic elements may also be oxidized by solutions of other metal salts; for example:
\[\ce{Cu}(s)+\ce{2AgNO3}(aq)\rightarrow \ce{Cu(NO3)2}(aq)+\ce{2Ag}(s) \nonumber \]
This reaction may be observed by placing copper wire in a solution containing a dissolved silver salt. Silver ions in solution are reduced to elemental silver at the surface of the copper wire, and the resulting Cu2+ ions dissolve in the solution to yield a characteristic blue color (Figure \(\PageIndex{4}\)).

Identify which equations represent redox reactions, providing a name for the reaction if appropriate. For those reactions identified as redox, name the oxidant and reductant.
- \(\ce{ZnCO3}(s)\rightarrow \ce{ZnO}(s)+\ce{CO2}(g)\)
- \(\ce{2Ga}(l)+\ce{3Br2}(l)\rightarrow \ce{2GaBr3}(s)\)
- \(\ce{2H2O2}(aq)\rightarrow \ce{2H2O}(l)+\ce{O2}(g)\)
- \(\ce{BaCl2}(aq)+\ce{K2SO4}(aq)\rightarrow \ce{BaSO4}(s)+\ce{2KCl}(aq)\)
- \(\ce{C2H4}(g)+\ce{3O2}(g)\rightarrow \ce{2CO2}(g)+\ce{2H2O}(l)\)
Solution
Redox reactions are identified per definition if one or more elements undergo a change in oxidation number.
- This is not a redox reaction, since oxidation numbers remain unchanged for all elements.
- This is a redox reaction. Gallium is oxidized, its oxidation number increasing from 0 in Ga(l) to +3 in GaBr3(s). The reducing agent is Ga(l). Bromine is reduced, its oxidation number decreasing from 0 in Br2(l) to −1 in GaBr3(s). The oxidizing agent is Br2(l).
- This is a redox reaction. It is a particularly interesting process, as it involves the same element, oxygen, undergoing both oxidation and reduction (a so-called disproportionation reaction). Oxygen is oxidized, its oxidation number increasing from −1 in H2O2(aq) to 0 in O2(g). Oxygen is also reduced, its oxidation number decreasing from −1 in H2O2(aq) to −2 in H2O(l). For disproportionation reactions, the same substance functions as an oxidant and a reductant.
- This is not a redox reaction, since oxidation numbers remain unchanged for all elements.
- This is a redox reaction (combustion). Carbon is oxidized, its oxidation number increasing from −2 in C2H4(g) to +4 in CO2(g). The reducing agent (fuel) is C2H4(g). Oxygen is reduced, its oxidation number decreasing from 0 in O2(g) to −2 in H2O(l). The oxidizing agent is O2(g).
This equation describes the production of tin(II) chloride:
\[\ce{Sn}(s)+\ce{2HCl}(g)\rightarrow \ce{SnCl2}(s)+\ce{H2}(g) \nonumber \]
Is this a redox reaction? If so, provide a more specific name for the reaction if appropriate, and identify the oxidant and reductant.
- Answer
-
Yes, a single-replacement reaction. Sn(s) is the reductant, HCl(g) is the oxidant.
Balancing Redox Reactions via the Half-Reaction Method
Redox reactions that take place in aqueous media often involve water, hydronium ions, and hydroxide ions as reactants or products. Although these species are not oxidized or reduced, they do participate in chemical change in other ways (e.g., by providing the elements required to form oxyanions). Equations representing these reactions are sometimes very difficult to balance by inspection, so systematic approaches have been developed to assist in the process. One very useful approach is to use the method of half-reactions, which involves the following steps:
- Write the two half-reactions representing the redox process.
- Balance all elements except oxygen and hydrogen.
- Balance oxygen atoms by adding H2O molecules.
- Balance hydrogen atoms by adding H+ ions.
- Balance charge1 by adding electrons.
- If necessary, multiply each half-reaction’s coefficients by the smallest possible integers to yield equal numbers of electrons in each.
- Add the balanced half-reactions together and simplify by removing species that appear on both sides of the equation.
- For reactions occurring in basic media (excess hydroxide ions), carry out these additional steps:
- Add OH− ions to both sides of the equation in numbers equal to the number of H+ ions.
- On the side of the equation containing both H+ and OH− ions, combine these ions to yield water molecules.
- Simplify the equation by removing any redundant water molecules.
- Finally, check to see that both the number of atoms and the total charges2 are balanced.
Write a balanced equation for the reaction between dichromate ion and iron(II) to yield iron(III) and chromium(III) in acidic solution.
\[\ce{Cr2O7^2- + Fe^2+ \rightarrow Cr^3+ + Fe^3+} \nonumber \]
Solution
Write the two half-reactions.
Each half-reaction will contain one reactant and one product with one element in common.
\(\ce{Cr2O7^2- \rightarrow Cr^3+}\)
Balance all elements except oxygen and hydrogen. The iron half-reaction is already balanced, but the chromium half-reaction shows two Cr atoms on the left and one Cr atom on the right. Changing the coefficient on the right side of the equation to 2 achieves balance with regard to Cr atoms.
\(\ce{Cr2O7^2- \rightarrow 2Cr^3+}\)
Balance oxygen atoms by adding H2O molecules. The iron half-reaction does not contain O atoms. The chromium half-reaction shows seven O atoms on the left and none on the right, so seven water molecules are added to the right side.
\(\ce{Cr2O7^2- \rightarrow 2Cr^3+ + 7H2O}\)
Balance hydrogen atoms by adding H+ions. The iron half-reaction does not contain H atoms. The chromium half-reaction shows 14 H atoms on the right and none on the left, so 14 hydrogen ions are added to the left side.
\(\ce{Cr2O7^2- + 14H+ \rightarrow 2Cr^3+ + 7H2O}\)
Balance charge by adding electrons. The iron half-reaction shows a total charge of 2+ on the left side (1 Fe2+ ion) and 3+ on the right side (1 Fe3+ ion). Adding one electron to the right side bring that side’s total charge to (3+) + (1−) = 2+, and charge balance is achieved.
The chromium half-reaction shows a total charge of (1 × 2−) + (14 × 1+) = 12+ on the left side (\(\ce{1 Cr2O7^2-}\) ion and 14 H+ ions). The total charge on the right side is (2 × 3+) = 6 + (2 Cr3+ ions). Adding six electrons to the left side will bring that side’s total charge to (12+ + 6−) = 6+, and charge balance is achieved.
\(\ce{Fe^2+ \rightarrow Fe^3+ + e-}\)
\(\ce{Cr2O7^2- + 14H+ + 6e- \rightarrow 2Cr^3+ + 7H2O}\)
Multiply the two half-reactions so the number of electrons in one reaction equals the number of electrons in the other reaction. To be consistent with mass conservation, and the idea that redox reactions involve the transfer (not creation or destruction) of electrons, the iron half-reaction’s coefficient must be multiplied by 6.
\(\ce{6Fe^2+ \rightarrow 6Fe^3+ + 6e-}\)
\(\ce{Cr2O7^2- + 6e- + 14H+ \rightarrow 2Cr^3+ + 7H2O}\)
Add the balanced half-reactions and cancel species that appear on both sides of the equation.
\[\ce{6Fe^2+ + Cr2O7^2- + 6e- + 14H+ \rightarrow 6Fe^3+ + 6e- + 2Cr^3+ + 7H2O} \nonumber \]
Only the six electrons are redundant species. Removing them from each side of the equation yields the simplified, balanced equation here:
\[\ce{6Fe^2+ + Cr2O7^2- + 14H+ \rightarrow 6Fe^3+ + 2Cr^3+ + 7H2O} \nonumber \]
A final check of atom and charge balance confirms the equation is balanced.
| Reactants | Products | |
|---|---|---|
| Fe | 6 | 6 |
| Cr | 2 | 2 |
| O | 7 | 7 |
| H | 14 | 14 |
| charge | 24+ | 24+ |
In acidic solution, hydrogen peroxide reacts with Fe2+ to produce Fe3+ and H2O. Write a balanced equation for this reaction.
- Answer
-
\[\ce{H2O2}(aq)+\ce{2H+}(aq)+\ce{2Fe^2+} \rightarrow \ce{2H2O}(l)+\ce{2Fe^3+} \nonumber \]
Summary
Chemical reactions are classified according to similar patterns of behavior. A large number of important reactions are included in three categories: precipitation, acid-base, and oxidation-reduction (redox). Precipitation reactions involve the formation of one or more insoluble products. Acid-base reactions involve the transfer of hydrogen ions between reactants. Redox reactions involve a change in oxidation number for one or more reactant elements. Writing balanced equations for some redox reactions that occur in aqueous solutions is simplified by using a systematic approach called the half-reaction method.
Footnotes
- 1 The requirement of “charge balance” is just a specific type of “mass balance” in which the species in question are electrons. An equation must represent equal numbers of electrons on the reactant and product sides, and so both atoms and charges must be balanced.
- 2 The requirement of “charge balance” is just a specific type of “mass balance” in which the species in question are electrons. An equation must represent equal numbers of electrons on the reactant and product sides, and so both atoms and charges must be balanced.
Glossary
- acid
- substance that produces H3O+ when dissolved in water
- acid-base reaction
- reaction involving the transfer of a hydrogen ion between reactant species
- base
- substance that produces OH− when dissolved in water
- combustion reaction
- vigorous redox reaction producing significant amounts of energy in the form of heat and, sometimes, light
- half-reaction
- an equation that shows whether each reactant loses or gains electrons in a reaction.
- insoluble
- of relatively low solubility; dissolving only to a slight extent
- neutralization reaction
- reaction between an acid and a base to produce salt and water
- oxidation
- process in which an element’s oxidation number is increased by loss of electrons
- oxidation-reduction reaction
- (also, redox reaction) reaction involving a change in oxidation number for one or more reactant elements
- oxidation number
- (also, oxidation state) the charge each atom of an element would have in a compound if the compound were ionic
- oxidizing agent
- (also, oxidant) substance that brings about the oxidation of another substance, and in the process becomes reduced
- precipitate
- insoluble product that forms from reaction of soluble reactants
- precipitation reaction
- reaction that produces one or more insoluble products; when reactants are ionic compounds, sometimes called double-displacement or metathesis
- reduction
- process in which an element’s oxidation number is decreased by gain of electrons
- reducing agent
- (also, reductant) substance that brings about the reduction of another substance, and in the process becomes oxidized
- salt
- ionic compound that can be formed by the reaction of an acid with a base that contains a cation and an anion other than hydroxide or oxide
- single-displacement reaction
- (also, replacement) redox reaction involving the oxidation of an elemental substance by an ionic species
- soluble
- of relatively high solubility; dissolving to a relatively large extent
- solubility
- the extent to which a substance may be dissolved in water, or any solvent
- strong acid
- acid that reacts completely when dissolved in water to yield hydronium ions
- strong base
- base that reacts completely when dissolved in water to yield hydroxide ions
- weak acid
- acid that reacts only to a slight extent when dissolved in water to yield hydronium ions
- weak base
- base that reacts only to a slight extent when dissolved in water to yield hydroxide ions

