1.8: Gaseous Ions
- Page ID
- 46532
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)It was proposed even as far back as the time of Ben Franklin and John Dalton that the forces between particles of matter must be electrical in some way. But because like charges repel one another, it was believed, wrongly, that bonds could not exist between identical atoms, whereas we now know that most common gases occur as diatomic molecules: H2, N2, 02, F2, Cl2, and so on. This one blunder led to nearly a half-century of confusion about molecular structure and atomic weights, during which it was thought that hydrogen gas was H instead of H2 water was HO instead of H2O, and oxygen had an atomic weight of 8 rather than 16. Electron pairs as the "glue" that holds atoms together in covalent bonds were not even proposed systematically until 1913, by G. N. Lewis; they were not explained theoretically for still another 20 years. Faraday's experiments showed that the charges on ions did occur naturally in fundamental pieces or units such that a mole of these charges equaled 1  , and Stoney named this elemental unit the electron. But Stoney's electron was not necessarily a particle that could be isolated and studied.
, and Stoney named this elemental unit the electron. But Stoney's electron was not necessarily a particle that could be isolated and studied.

The people who first showed that electrons were real particles that could be added to or removed from atoms were physicists studying the effects of electricity on gases. They found that if they set up an electrical potential of 10,000 volts between two electrodes in a sealed tube (a Crookes tube) containing gas at low pressure, they observed a glow discharge (Figure 1-11). This discharge is what makes neon signs glow. The electrical potential strips electrons from atoms of the gas, sending the electrons streaming toward the anode and positive ions toward the cathode. These moving electrons (the cathode rays) can be detected by watching the flashes of light on a zinc sulfide screen placed in the tube. If a lightweight pinwheel is set up in the path of the electrons inside the tube, the electrons even make the pinwheel rotate. On their way to the anode, the cathode rays strike other atoms of the gas, causing the emission of light in a glow discharge. The color of the glow discharge will vary, depending on the gas used· inside the tube.
If a metal plate with a slit is placed in front of the cathode, then the electrons in the cathode ray will be confined to a thin beam. This beam is deflected by electric and magnetic fields in a way that indicates that the particles in the beam carry a negative charge. The relative amount of bending of the canal rays (positive ions) and cathode rays (negative electrons) shows that the cathode ray particles are extremely light, whereas the positive ions are roughly as heavy as the original atoms from which they came. The exact nature of the canal rays depends on what gas is used in the tube, but the cathode rays are the same for all gases. J. J. Thomson (1856- 1940) suggested that the particles in the cathode rays might in fact be Stoney's "electrons," and in 1897 he found a way to use the deflection of the beam by electric and magnetic fields to calculate the charge-to-mass ratio (elm) of the particles. He found that
-
 = 1.76 x 108 coulombs g-1
= 1.76 x 108 coulombs g-1

Assume that Thomson's cathode ray particles are in fact the same as Stoney's and Faraday's electrons, and that 1 is a mole of electrons. Calculate the mass of one electron. is a mole of electrons. Calculate the mass of one electron. |
|
Solution The charge on one electron is
|

A modern descendant of the Crookes tube and Thomson's apparatus is the mass spectrometer (Figure 1-12). It is a valuable research tool for measuring the mass per unit charge of any substance that can be given a positive charge. Mass spectrometry offers the most direct measurement of atomic weights of elements, and it is the method by which isotopes can be both identified and separated. By looking at the masses of the fragments into which molecules are broken down during electron bombardment in the spectrometer, organic chemists can obtain useful information about the molecular structure of a substance. (During the development of the atomic bomb in World War II, mass spectrometry was used to separate fissionable 235U from 238U, although the extremely low pressures that mass spectrometry requires were not practical for large-scale production.)
Although the ratio of electron charge to electron mass was measured in 1897 by Thomson, the charge itself was not measured until 1911 , when Robert A. Millikan (1868-1953) obtained the charge by the ingenious experiment illustrated in Figure 1-13. He used x rays to irradiate a spray of tiny oil droplets between two chargeable plates. Electrons from ionization of the air around the drops adhered to the drops, giving them one, two, or more electron charges. Millikan measured first the rate of free fall of the charged drops through air of known viscosity. Then he measured the voltage across the plates that was sufficient to suspend the drops motionless between the plates. He calculated that the charge on anyone drop was always an integral multiple of 1.6022 X 10-19 coulomb, and he concluded correctly that this was the charge on a single electron.
Example 20 actually was presented the wrong way around. We can solve it only because we know the value of Avogadro's number, whereas in fact Millikan's results furnished one way of calculating Avogadro's number.
| Assume that you do not know the value of Avogadro's number, but that you recognize that the faraday is the charge necessary to reduce 1 mole of Na+ ions, with one of Millikan's electrons combining with each ion. Calculate the number of ions in a mole, or Avogadro's number. |
|
Solution The charge on one electron is
|
Contributors and Attributions
R. E. Dickerson, H. B. Gray, and G. P. Haight, Jr. Content was used from "Chemical Principles", an introductory college-level text for General Chemistry with permission of the Caltech library and Harry B. Gray, on behalf of the authors.


 =
= 
 = 0.910 x 10-27 g
= 0.910 x 10-27 g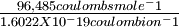 = 6.022 x 1023 ions mole-1
= 6.022 x 1023 ions mole-1