1.7: Ions in Solution
- Page ID
- 46531
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Although salts are hard to melt and even harder to vaporize, many can be dissolved easily in a polar liquid such as water. The reason for this is simple. The water molecules help to dismantle the salt crystal, since the partial positive and negative charges on the polar water molecules (Figure 1-4) provide a substitute for the positive and negative charges that were present in the crystal lattice. Figure 1-7 illustrates what happens when a crystal such as sodium chloride is dissolved in water. Each positively charged Na+ is surrounded by water molecules with their negatively charged oxygens turned toward it, and each negatively charged Cl- ion is surrounded by water molecules with their positively charged hydrogens closest. The ions from the salt crystal are said to be hydrated. If the stability that hydration gives the ions in solution is greater than the stability of the crystal lattice, then the salt will dissolve. Sodium chloride is a familiar example of a soluble salt. In contrast, if the hydration energy is too small, then the crystal will be the more stable form, and it will not dissolve in water. Silver chloride (AgCl) and barium sulfate (BaS04) are examples of insoluble salts. When a salt crystal dissolves, it does not simply come apart into ions; it is taken apart by the molecules of the liquid in which it is dissolved (the solvent). This is why salts will not dissolve in nonpolar liquids such as gasoline (octane, C8H18); there are no charges on the solvent molecules to make up for the loss of charge attractions within the crystalline salt.

Salt solutions conduct electricity, and this property was extremely important early in the development of theories of chemical bonding. Electrical conduction in metals takes place by means of moving electrons; the metal ions remain in place. Crystalline salts do not conduct electricity at all, but if the salt is melted, then positive ions can migrate one way through the liquid and negative ions can move the other way in the presence of an electric field. This mobility of ions is even greater if the salt is dissolved in water and the ions consequently are hydrated.
Some of the first concrete ideas about the nature of chemical bonding came from the electrolysis experiments of the English scientist Michael Faraday (1791-1867). (Electrolysis means "breaking apart with electricity.") If sodium chloride is melted (above 801°C) and if two electrodes (the cathode and the anode) are inserted into the melt as shown in Figure 1-8 and an electric current is passed through the molten salt, then chemical reactions take place at the electrodes: Sodium ions migrate to the cathode, where electrons enter the melt, and are reduced to sodium metal:


\[Na^+ + e^-(from\; cathode) → Na\]
Chloride ions migrate the other way, toward the anode, give up their electrons to the anode, and are oxidized to chlorine gas:
\[Cl^- → \frac{1}{2} Cl_{2} + e^-(to\; anode)\]
The overall reaction is the breakdown of sodium chloride into its elements:
\[Na^+ + CI^- → Na + \frac{1}{2}Cl_2\]
Sodium ions are reduced and chloride ions are oxidized. Electrolysis can also be carried out by passing electric current through solutions of salts (Figure 1-9). If a solution of sodium chloride in water is electrolyzed, chlorine gas is given off at the anode as in the case of molten sodium chloride, but the cathode product is hydrogen gas rather than metallic sodium:
\[Na^+ + Cl^- + H_2O \rightarrow Na + \frac{1}{2} Cl_2 + \frac{1}{2} H_2 + OH^- \label{1-1}\]
This is the same result that would be obtained if liquid sodium chloride was first electrolyzed to give metallic sodium:
\[Na^+ + Cl^- → Na + \frac{1}{2} Cl_2 \label{1-2}\]
and the sodium was then dumped into water:
\[Na + H_2O → Na^+ + \frac{1}{2}H_2 + OH^- \label{1-3}\]
Equation \(\ref{1-1}\) is just the sum of Equations \(\ref{1-2}\) and \(\ref{1-3}\), since the sodium metal that is produced in Equation \(\ref{1-2}\) is used up in Equation \(\ref{1-3}\). There is nothing mysterious about the different cathode products during electrolysis of sodium chloride in a melt or in solution, If water is present, some of the H2O molecules will be dissociated into H+ and OH- ions. Because H+ has a greater affinity for electrons than Na+ does, the H+ ions will take electrons away from metallic sodium, making the anode product H2 rather than Na, and leaving Na+ ions in solution. In contrast, Cu2+ ions have a greater affinity for electrons than H+ ions do, so the anode product of electrolysis of CuCl2 is metallic copper, whether the process is carried out in the melt or in solution (Figure 1-9). Typical products of electrolysis of solutions and melts are given in Table 1-8. Electrochemical reactions and cells are discussed in detail in Chapter 19. At the moment, we are focusing on what electrochemical reactions tell us about chemical bonding.
| Electrolytett | Cathode Producttt | Anode Product |
| Sulfuric acid (H2SO4) in H2Ott | H2tt | O2 |
| Sodium sulfate (Na2SO4) in H2Ott | H2tt | O2 |
| Sodium chloride (NaCl) in H2Ott | H2tt | Cl2 |
| Potassium iodide (Kl) in H20tt | H2tt | I2 |
| Copper sulfate (Cu2SO4) in H20tt | Cutt | O2 |
| Silver nitrate (AgNO3) in H2Ott | Agtt | O2 |
| Mercuric nitrate [Hg(NO3)2] in H20tt | Hgtt | O2 |
| Lead nitrate [Pb(NO3)2] in H20tt | Pbtt | O2 and some PbO2 |
| Molten lye (NaOH); not in H2Ott | Natt | O2 |
- Passing the same quantity of electricity through a cell always leads to the same amount of chemical change for a given reaction. The weight of an element deposited or liberated at an electrode is proportional to the amount of electricity that is passed through.
- It takes 96,485 coulombs of electricity to deposit or liberate 1 mole of a substance that gains or loses one electron during the cell reaction. If n electrons are involved in the reaction, then 96,485n coulombs of electricity are required to liberate a mole of product.
The quantity 96,485 coulombs of electricity has become known as 1 faraday in his honor, and has been given the symbol  . Faraday's laws become self-evident when you realize that 1
. Faraday's laws become self-evident when you realize that 1  is simply the charge on 1 mole of electrons, or 6.022 X 1023 electrons. The scale-up factor of 6.022 X 1023 from molecules to moles is paralleled by the same scale-up factor from 1 electron charge to 1
is simply the charge on 1 mole of electrons, or 6.022 X 1023 electrons. The scale-up factor of 6.022 X 1023 from molecules to moles is paralleled by the same scale-up factor from 1 electron charge to 1  of charge. At the time, of course, Faraday knew neither the value of Avogadro's number nor the charge on an electron. His experiments did tell him, however, that charges on ions came in multiples of a fundamental unit, such that 96,485 coulombs corresponded to a mole of these units. The word electron first appeared in 1881, when the British physicist G. J. Stoney coined it to denote this fundamental unit of ionic charge. Its application to a real negatively charged particle came a decade later.
of charge. At the time, of course, Faraday knew neither the value of Avogadro's number nor the charge on an electron. His experiments did tell him, however, that charges on ions came in multiples of a fundamental unit, such that 96,485 coulombs corresponded to a mole of these units. The word electron first appeared in 1881, when the British physicist G. J. Stoney coined it to denote this fundamental unit of ionic charge. Its application to a real negatively charged particle came a decade later.
Write equations for the reactions that occur when current is passed through molten NaCl. How many grams of sodium and chlorine are released when 1  of charge is passed through the cell? of charge is passed through the cell? |
|
Solution The cathode reaction is Na+ + e- → Na, and the anode reaction is Cl-→ |
How many grams of magnesium metal and chlorine gas are released when 1  of electricity is passed through an electrolytic cell containing molten magnesium chloride, MgC12? of electricity is passed through an electrolytic cell containing molten magnesium chloride, MgC12? |
|
Solution The cathode reaction is Mg2+ + 2e- → Mg, and the anode reaction is this: 2Cl-→ Cl2 + 2e-. Since two electrons are required to reduce each ion of Mg2+, 1 mole of electrons will be sufficient to reduce half a mole of magnesium ions, depositing 12.153 g of magnesium. (The atomic weight of magnesium is 24.305 g mole-1.) As in Example 16, 1 mole of Cl- ions is oxidized, liberating half a mole or 35.453 g of Cl2 gas. |
| The main commercial source of aluminum metal is the electrolysis of molten salts of Al3+. How many faradays of charge, and how many coulombs, must be passed through the melt to deposit 1 kg of metal? |
|
Solution One kilogram of aluminum is 1000 g/26.98 g mole-1, or 37.06 moles. Since each atom of aluminum deposited requires three electrons, 37.06 moles will require 3 X 37.06, or 111.2, moles of electrons. Hence 111.2 |
| Electron flow at the rate of 1 coulomb per second (coulomb sec-1) is a current of 1 ampere (A). Currents in industrial electrolytic production of aluminum are ordinarily in the range of 20,000 to 50,000 A. If a cell is operated at 40,000 A (40,000 coulombs sec-1), how long will it take to produce the kilogram of aluminum metal mentioned in Example 18? |
|
Solution The time required will be
|

 ) for each mole of copper. Each faraday is enough to oxidize 1 mole of Cl- ions to
) for each mole of copper. Each faraday is enough to oxidize 1 mole of Cl- ions to  mole of Cl2 gas. (b) Only 1
mole of Cl2 gas. (b) Only 1 of charge is required to reduce 1 mole of Ag+ ions to metallic silver. since the ionic charge on Ag+ is only +1. Chlorine gas is liberated at the same rate per faraday as before.
of charge is required to reduce 1 mole of Ag+ ions to metallic silver. since the ionic charge on Ag+ is only +1. Chlorine gas is liberated at the same rate per faraday as before.Faraday's laws are represented diagrammatically in Figure 1-10. We have been using these laws with a prior knowledge of the charges on different ions, and the knowledge that 96,485 coulombs is the total charge on 6.022 X 1023 electrons. History actually operated in reverse: Faraday and others used electrolysis experiments to find out what the charges on ions were. The reasoning used is illustrated in Table 1-9. If twice as much electricity is required to liberate a mole of copper as a mole of silver (assuming that you know the atomic weights of the two metals and can calculate the weights of a mole of each), then the copper ion must have twice the charge of the silver ion. In Table 1-9, the number of faradays of charge required to liberate 1 mole of an element is the same as the number of charges, positive or negative, on the ion.
|
Product of electrolysis |
Electrode |
Faradays per mole of atoms deposited |
Ion in solution |
|---|---|---|---|
| Silver (Ag) | Cathode | 1a | Ag+ |
| Chlorine (Cl2) | Anode | 1 | Cl- |
| Copper (Cu) | Cathode | 2 | Cu2+ |
| Hydrogen (H2) | Cathode | 1 | H+ |
| Iodine (I2) | Anode | 2 | I- |
| Oxygen (O2)b | Anode | 2 | O2- |
| Zinc (Zn) | Cathode | 2 | Zn2+ |
a For example, electrolysis of silver nitrate solution for 1 hour by using a current of 0.5 A deposits 2.015 g of silver; 2.015/107.9 = 0.0187 mole of silver.
(0.5 coulomb sec^-1) x 3600 sec = 0.0187 
-
- 96.485 coulombs
 -1
-1
- 96.485 coulombs
b Actually, oxygen (02) is produced by a complicated electrode reaction. The species O2- can exist in molten oxides, but in water 02- becomes 2OH- by reaction with a water molecule.
Contributors and Attributions
R. E. Dickerson, H. B. Gray, and G. P. Haight, Jr. Content was used from "Chemical Principles", an introductory college-level text for General Chemistry with permission of the Caltech library and Harry B. Gray, on behalf of the authors.


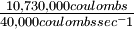 = 268 sec or 4.5 min
= 268 sec or 4.5 min