22.9: Geometry of Complexes
- Page ID
- 49653
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The geometry of a complex is governed almost entirely by the coordination number. We will consider only the most common coordination numbers, namely, 2, 4, and 6.
Coordination number = 2
Complexes with two ligands are invariably linear. The best-known examples of such compounds are Ag(I) and Au(I) complexes such as
2%25E2%2580%2593.jpg?revision=1&size=bestfit&width=168&height=19)
2%252B.jpg?revision=1&size=bestfit&width=230&height=103)
Both of these complexes are important. The Au(CN)2– complex is used to extract minute gold particles from the rock in which they occur. The crushed ore is treated with KCN solution and air is blown through it:
\[ 4 \text{Au} (s) + 8 \text{CN}^{-} (aq) + \text{O}_{2} (g) + 2 \text{H}_{2} \text{O} (l) \rightarrow 4 \text{[Au(CN)}_{2} \text{]}^{-} (aq) + 4 \text{OH}^{-} (aq) \label{1} \]
The resultant complex is water soluble. The silver complex is also water soluble and affords a method for dissolving AgCl, which is otherwise very insoluble.
\[ \text{AgCl} (s) + 2 \text{NH}_{3} (aq) \rightarrow \text{[Ag(NH}_{3} \text{)}_{2} \text{]}^{+} (aq) + \text{Cl}^{-} (aq) \nonumber \]
This reaction is often used in the laboratory to be sure a precipitate is AgCl(s).
42%252B_(square_planar)_and_Zn(NH3)42%252B_(tetrahedral)_.jpg?revision=1)
Coordination number = 4
Two geometries are possible for this coordination number. Some complexes, like the [Pt(NH3)4]2+ ion shown in Figure \(\PageIndex{1}\), are square planar, while others, like Cd(NH3)42–, are tetrahedral. Most of the four-coordinated complexes of Zn(II), Cd(II), and Hg(II) are tetrahedral, while the square planar arrangement is preferred by Pd(II), Pt(II), and Cu(II) complexes.
Because the square planar geometry is less symmetrical than the tetrahedral geometry, it offers more possibilities for isomerism. A well-known example of such isomerism is given by the two square planar complexes
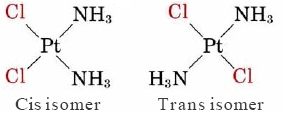2.jpg?revision=1&size=bestfit&width=284&height=113)
These two isomers are called geometrical isomers. That isomer in which two identical ligands are next to each other is called the cis isomer, while that in which they are on opposite sides is called the trans isomer. Though these two isomers have some properties which are similar, no properties are identical and some are very different. For example, the cis isomer of the above complex is used as an anti-tumor drug to treat cancerous cells. The trans form, by contrast, shows no similar biological activity.
It is worth noting that cis-trans isomerism is not possible in the case of tetrahedral complexes. As you can quickly verify by examining any three-dimensional tetrahedral shape, any given corner of a tetrahedron is adjacent to the other three. Since all the corners are cis to each other, none are trans.
Coordination number = 6
When there are six ligands, the geometry of the complex is almost always octahedral, like the geometry of SF6, or of [Cr(H2O)6]3+. All ligands are equidistant from the central atom, and all ligand-metal-ligand angles are 90°. An octahedral complex may also be thought of as being derived from a square planar structure by adding a fifth ligand above and a sixth below on a line through the central metal ion and perpendicular to the plane.
4Cl2_.jpg?revision=1)
The octahedral structure also gives rise to geometrical isomerism. For example, two different compounds, one violet and one green, have the formula [Co(NH3)4Cl2]Cl. The violet complex turns out to have the cis structure and the green one trans, as shown in Figure \(\PageIndex{2}\).


