21.4: Bohr Theory of the Atom
- Page ID
- 49639
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
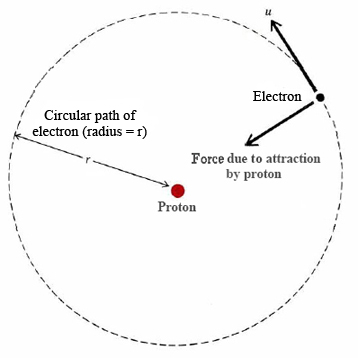
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In a classic paper published in 1913, the young Niels Bohr, then working with Rutherford in Manchester, England, proceeded to show how Rydberg’s formula could be explained in terms of a very simple model of the hydrogen atom. The model was based on the nuclear view of atomic structure which had just been proposed by Rutherford. Bohr’s model is shown in Figure \(\PageIndex{1}\). An electron of charge –e and mass \(m\) moves around a heavy nucleus of charge +e. Ordinarily the electron would move in a straight line, but the attraction of the nucleus bends its path so that it moves with a constant velocity \(u\) in a perfect circle of radius r around the nucleus. The situation and the mathematics are very similar to that of a planet arcing round the sun. The major difference is that instead of the force of gravity there is an electrostatic force of attraction \(F\) between the proton and the electron described by Coulomb’s law:
\[F=k\frac{e^{2}}{r^{2}} \label{1} \]
where \(k\) has the value 8.9876 × 109 J m C–2.
Expressions for both the kinetic and potential energies of the electron can be derived using Equation \(\ref{1}\) and the principles of elementary physics. Such a derivation can be found in most introductory physics texts. The two expressions are
\[E_{k}=\frac{1}{2}mu^{2}=\frac{1}{2}k\frac{e^{2}}{r} \label{2} \]
and
\[E_{p}=-k\frac{e^{2}}{r} \label{3} \]
If these are added together, we obtain a simple formula for the total energy of the electron:
\[\begin{align} E &=E_{k}+E_{p} \\[4pt] &=-\frac{1}{2}k\frac{e^{2}}{r} \label{4} \end{align} \]
If we now insert the known values of \(e\) and \(k\), we have the result
\[ \begin{align} E &= -\frac{1}{2}\times\frac{8.9876 \times 10^{9} \text{ J m C}^{-2}\times(1.6022 \times 10^{-19} \text{ C})^{2}}{r} \\[4pt] &=-\frac{1.1536 \times 10^{-28} \text{ J M} }{r} \label{5} \end{align} \]
From Equation \(\ref{5}\) we see that the total energy of the electron is very negative for an orbit with a small radius but increases as the orbit gets larger.
In addition to suggesting the planetary model just described, Bohr also made two further postulates which enabled him to explain the spectrum of hydrogen. The first of these was the suggestion that an electron of high energy circling the nucleus at a large radius can lose some of that energy and assume an orbit of lower energy closer to the nucleus. The energy lost by the electron is emitted as a photon of light of frequency \(\nu\) given by Planck’s formula
\[\Delta E = h\upsilon \label{6} \]
where \(ΔE\) is the energy lost by the electron.
Bohr’s second postulate was that only certain orbits are possible to the electron in a hydrogen atom. This enabled him to explain why it is that only light of a few particular frequencies can be emitted by the hydrogen atom. Since only a limited number of orbits are allowed, when an electron shifts from an outer to an inner orbit, the photon which emerges cannot have just any frequency but only that frequency corresponding to the energy difference between two allowed orbits.
According to Bohr’s theory two of the allowed orbits in the hydrogen atom have radii of 52.918 and 211.67 pm. Calculate the energy, the frequency, and the wavelength of the photon emitted when the electron moves from the outer to the inner of these two orbits.
Solution
Labeling the outer orbit 2 and the inner orbit 1, we first calculate the energy of each orbit from Equation \(\ref{5}\):
\[E_{2}=-\dfrac{1.1536\times10^{-28} \text{Jm}}{211.67\times10^{-12} \text{m}}=-0.54500 \text{aJ} \nonumber \]
\[E_{1}=-\dfrac{1.1536\times10^{-28} \text{Jm}}{52.918\times10^{-12} \text{m}}=-2.1780\, \text{aJ} \nonumber \]
Thus
\[ \Delta E = – 0.545 00 \text{aJ} – (– 2.1780 \text{aJ}) = 1.6330\, \text{aJ} \nonumber \]
Using Equation \(\ref{6}\), we now have
\[\upsilon=\dfrac{\Delta E}{h}=\dfrac{1.6330\times10^{-18}\text{ J}}{6.6262\times10^{-34} \text{ J s}}=2.4645\times10^{15} \text{ s}^{-1}=2.4645 \text{ PHz} \nonumber \]
Finally \( \lambda = \dfrac{c}{\upsilon} = 1.2164 \times 10^{-7} \text{ m} = 121.64 \text{ nm} \). In order to predict the right frequencies for the lines in the hydrogen spectrum, Bohr found that he had to assume that the quantity \(mur\) (called the angular momentum by physicists) needed to be a multiple of \(h/2π\). In other words the condition restricting the orbits to only certain radii and certain energies was found to be
\[mur=\frac{nh}{2\pi} \qquad \label{7} \]
where could have the value 1, 2, 3, etc.
By manipulating both Equations \(\ref{7}\) and \(\ref{2}\), it is possible to show that this restriction on the angular momentum restricts the radii of orbits to those given by the expression
\[ r = \frac{n^{2}h^{2}}{4\pi^{2}mke^{2}} \qquad n = 1, 2, 3, \cdots \label{8} \]
If the known values of h, m, k, and e are inserted, this formula reduces to the convenient form
\[ r = n^2 \times 52.918 \text{ pm} \qquad n = 1, 2, 3, \cdots \label{9} \]
Bohr’s postulate thus restricts the electron to orbits for which the radius is 52.9 pm, 22 × 52.9 pm, 32 × 52.9 pm, and so on.
If we substitute Equation \(\ref{8}\) into Equation \(\ref{4}\), we arrive at a general expression for the energy in terms of n:
\[E=-\frac{1}{2}k\frac{e^{2}}{r}=-\frac{1}{2}ke^{2}\times\frac{4\pi^{2}mke^{2}}{n^{2}h^{2}} =\frac{2\pi^{2}k^{2}e^{4}m}{n^{2}h^{2}} \label{10} \] Again substituting in the known values for all the constants, we obtain \[E=-\frac{2.1800 \text{ aJ}}{n^{2}} \label{11} \]
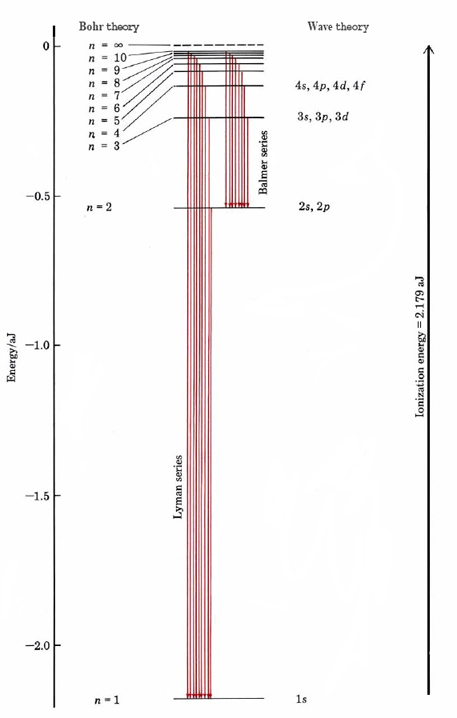
The integer \(n\) thus determines how far the electron is from the nucleus and how much energy it has, just as the principal quantum number \(n\) described previously.
Using Equation \(\ref{10}\) or \(\ref{11}\) find the ionization energy of the hydrogen atom.
Solution
The ionization energy of the hydrogen atom corresponds to the energy difference between the electron in its innermost orbit (n = 1) and the electron when completely separated from the proton. For the completely separated electron r = ∞ (infinity) and so does n. Thus
\[E_{1}=-\dfrac{2.1800 \text{aJ}}{1^{2}}=-2.1800\text{aJ} \nonumber \]
and
\[E_{\infty}=-\dfrac{2.1800 \text{aJ}}{\infty^{2}}=0.0000\text{aJ} \nonumber \]
The energy difference is thus
\[\Delta E=E_{infty}-E_{1}=2.1800 \text{aJ} \nonumber \]
which is the ionization energy per atom. On a molar basis the ionization energy is the Avogadro constant times this quantity; namely,
\[2.1800 \times 10^{-18} \text{J} \times 6.0221 \times 10^{23} \text{mol}^{-1} = 1312.8 \text{ kJ mol}^{-1}\ n\nonumber \]
Note: In an atom, the electronic configuration of lowest energy is called the ground state while other configurations are called excited states.
We can now derive Rydberg’s experimental formula from Bohr’s theory. Suppose an electron moves from an outer orbit for which the quantum number is n2 to an inner orbit of quantum number n1. The energy lost by the electron and emitted as a photon is then given by
\[\Delta E=E_{2}-E_{1}= – 2.1800 \text{ aJ} \left(\frac{1}{n_{2}^{2}}-\frac{1}{n_{1}^{2}}\right) = 2.1800 \text{ aJ} \left(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right) \label{12} \]
However,
\[\Delta E=h\upsilon=\frac{hc}{\lambda} \label{13} \]
where \(λ\) is the wavelength of the photon. Combining Eqs. \(\ref{2}\) and \(\ref{3}\), we obtain
\[\frac{1}{\lambda}=\frac{2.1800 \text{ aJ}}{hc}\left(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right) \nonumber \]
or
\[\frac{1}{\lambda}=1.0975\times10^{7}m^{-1} \left(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right) \label{14} \]
This expression is of exactly the same form as that found experimentally by Rydberg with a value for R∞ of 1.0974 × 107 m–1, very close to the experimental value of 1.097 094 × 107 m–1. Even better agreement can be obtained if allowance is made for the fact that the nucleus is not stationary but that the electron and nucleus revolve around a common center of gravity.
Calculate the wavelength of the light emitted when the electron in a hydrogen atom drops from the n = 3 to the n = 1 orbit. In what region of the spectrum does this spectral line lie? To what series does it belong?
Solution
From Equation \(\ref{14}\) we find
\[\dfrac{1}{\lambda}=1.0975\times10^{7}m^{-1}\times\left(1-\dfrac{1}{9}\right)=9.7547\times10^{6}m^{-1} \nonumber \]
giving \(\lambda = 102.51 \text{ nm} \). This is the second line in the Lyman series and lies in the far ultraviolet. The experimentally determined wavelength is 102.573 nm.
Bohr’s success with the hydrogen atom soon led to attempts both by him and by others to extend the same model to other atoms. On the qualitative level these attempts met with some success, and a general picture of electrons occupying orbits in successive levels and sub-levels, similar to that shown in Figure 5.2, began to emerge. On the quantitative level, however, all attempts to calculate accurate values for the energies of the electrons in their quantized orbitals were dismal failures. It was not until Schrödinger’s introduction of wave mechanics in 1926 that these difficulties could be resolved. Suddenly, it seemed, everything fell into place. Since then virtually every line in the spectrum of every element has been accounted for theoretically. As a result, we now have a very exact, though mathematically rather complex, picture of the behavior of electrons in both the ground state and in excited states of atoms. In particular, the study of atomic spectra has allowed us to determine the ionization energies of all the elements very accurately.
Details of the spectra of polyelectronic atoms are complex, and so we will consider only one example: sodium. Excited states of sodium may be obtained by increasing the energy of the atom so that the 3s valence electron occupies the 3p, 3d, 4s, 4p, 4d, 4f or some other orbital. By contrast with the hydrogen atom, however, a sodium atom has other electrons which shield the valence electron from nuclear charge, and this shielding is different for each different orbital shape (s, p, d, f, etc.). Consequently the energy of an excited sodium atom whose electron configuration is 1s22s22p64s1 is not the same as that of an excited sodium atom whose configuration is 1s22s22p64p1. Different shielding of the outermost (4s or 4p) electron results in a different energy. Because of this, four formulas are needed to describe the energy of the sodium atom—one for each of the orbital shapes available to the outermost electron:
\[\begin{align*} E_{ns} & =\frac{2.1800 \text{ aJ}}{(n-a_{s})^{2}}\\E_{np} & =\frac{2.1800 \text{ aJ}}{(n-a_{p})^{2}}\\ E_{nd} &= \frac{2.1800 \text{ aJ}}{(n-a_{d})^{2}}\\ E_{nf} & = \frac{2.1800 \text{ aJ}}{(n-a_{f})^{2}} \end{align*} \nonumber \]
In all these equations n represents the principal quantum number. It must be 3 or greater since the electron is in the 3s orbital to begin with. The different shielding requires a different correction for each type of orbital: as = 1.36; ap = 0.87; ad = 0.012; and af = 0.001.
Because there are four different sets of energy levels, the number of transitions between levels (and hence the number of lines in the spectrum) is larger for sodium than for hydrogen. Early spectroscopists were able to distinguish four different types of lines, which they labeled the sharp, principal, diffuse, and fundamental series. It is from the abbreviation of these terms that we have obtained the modern symbols s, p, d, and f.
As most readers will know, when almost any sodium compound is held in a Bunsen burner, it imparts a brilliant yellow color to the flame. This yellow color corresponds to the most prominent line in the sodium spectrum. Its wavelength is 589 nm. On the atomic scale this line is caused by the sodium atom moving from an excited state (in which the valence electron is in a 3p orbital) to the ground state (in which the electron is in a 3s orbital). Using the above equations we can obtain approximate values for the two energies involved in the transition:
\[E_{3p}=\frac{2.1800 \text{ aJ}}{(3-0.87)^{2}}=-0.4805\, \text{ aJ} \nonumber \]
and
\[E_{3s}=\dfrac{2.1800 \text{ aJ}}{(3-1.36)^{2}}=-0.8105\, \text{ aJ}. \nonumber \]
Thus \(\Delta E= 0.3300 \text{ aJ}\) giving \(\lambda = \dfrac{hc}{\Delta E}=602 \text{ nm}\) This agrees approximately with the experimental result. Another feature of the sodium spectrum deserves mention. Careful observation reveals that the yellow color of sodium is actually due to two closely spaced lines (a doublet). One has a wavelength of 588.995 nm, and the other is at 589.592 nm. When the electron is in a 3p orbital, its spin can be aligned in two ways with respect to the axis of the orbital. The small difference in energy between these two orientations results in two slightly different wavelengths


