13.13: The Molecular View of Equilibrium
- Page ID
- 49535
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In other sections, we show that equilibrium constants exist, how they can be determined, and how they can be used, but we have not explained why they are sometimes large and sometimes small. In order to answer this and related questions we must switch our point of view from the macroscopic to the microscopic level.
The cis-trans isomerism of difluoroethene provides a simple example for examination on the molecular level. As we saw earlier, if 1 mol cis isomer of this compound is heated to 623 K, it is gradually transformed into the equilibrium mixture of ⅔ mol cis isomer and ⅓ mol trans isomer. From a macroscopic point of view, we might conclude that the reaction stops once equilibrium is attained, but on the microscopic level, such a statement is obviously untrue.
As cis molecules move around a container at 623 K, they occasionally suffer a collision with sufficient energy to flip them over to the trans conformation ( for a microscopic view of this process, see Figure \(\PageIndex{1}\) ). This conversion process does not suddenly stop when equilibrium has been attained. There are plenty of cis molecules present in the equilibrium mixture, and they continue to collide with their fellow molecules and hence to flip over from the cis to the trans conformation. Thus the forward reaction
\[cis-\text{C}_2\text{H}_2\text{F}_2 \rightarrow trans-\text{C}_2\text{H}_2\text{F}_2 \nonumber \]
must continue to occur in the equilibrium mixture.
If this were the only reaction taking place in the flask, the eventual result would be that all the cis isomer would be converted to the trans isomer and no equilibrium mixture would result. This does not happen because the reverse reaction
\[trans-\ce{C_{2}H_{2}F_{2} \rightarrow} cis-\ce{C_{2}H_{2}F_{2}} \nonumber \]
is also occurring at the same time. The trans molecules in the equilibrium mixture are also continually being bombarded by their fellow molecules. Many of these collisions have sufficient energy to flip the trans molecule back into the cis form. Thus cis molecules are not only being consumed but also being produced in the flask. The concentration of the cis molecules remains constant because the rate at which they are being consumed is exactly balanced by the rate at which they are being produced.
In other words, for every cis molecule which flips to the trans conformation in one part of the container, there will be on the average a molecule of trans isomer flipping in the reverse direction in another part of the container. This constant reshuffle of molecules between the cis and the trans forms can then continue indefinitely without any net change in the concentration of either species.
This molecular interpretation of equilibrium is not confined to the particular example of cis-trans isomerism or even just to chemical reactions. In the section on phase transitions we describe vapor-liquid equilibria in which the condensation of vapor just balanced the evaporation of liquid. Any state of equilibrium corresponds to a situation in which the rate at which the forward reaction is occurring is exactly equal to the rate at which the reverse reaction is occurring. Since these rates are equal, there is no net change in the concentration of any of the reactants or products with time. Because an equilibrium corresponds to a balance between the forward and the reverse reaction in this way, we use double arrows (\(\rightleftharpoons\)) in the equation.
As another example of chemical equilibrium, let us take a 0.001 M solution of acetic acid at 25°C. As seen in the section on weak acids, slightly more than 10 percent of the acetic acid molecules in this solution have ionized according to the equation
\[\text{CH}_3\text{COOH} + \text{H}_2\text{O} \rightleftharpoons \text{CH}_3\text{COO}^{-} + \text{H}_3\text{O}^{+} \nonumber \]
Although the concentrations of all species in this solution remain constant with time, this does not mean that acetic acid molecules have stopped transferring protons to water molecules. The concentrations remain constant because the reverse reaction (transfer of a proton from a hydronium ion to an acetate ion) is occurring at the same rate as the forward reaction. For every hydronium ion produced by a proton transfer somewhere in the solution, another hydronium ion is losing its proton somewhere else. The net result is that the concentration of the hydronium ion remains constant, and with it the concentrations of the other species involved.
The microscopic view of equilibrium as a constant reshuffle of chemical species is often given a special name and referred to as a dynamic equilibrium. It is important to realize that once a dynamic equilibrium has been set up, a particular atom will sometimes turn up as part of one of the product molecules and sometimes as part of one of the reactant molecules.
In the ionization equilibrium of acetic acid just considered, suppose for the sake of argument that we could identify a particular oxygen atom in some way. If we could now follow the history of this atom, we would find that it would sometimes form part of an acetic acid molecule, CH3CO*OH and sometimes part of an acetate ion, CH3CO*O–. Since the acid is about 10 percent ionized, we would find on the average that our labeled oxygen would spend only 10 percent of its time as part of an acetate ion and the remaining 90 percent as part of an acetic acid molecule.
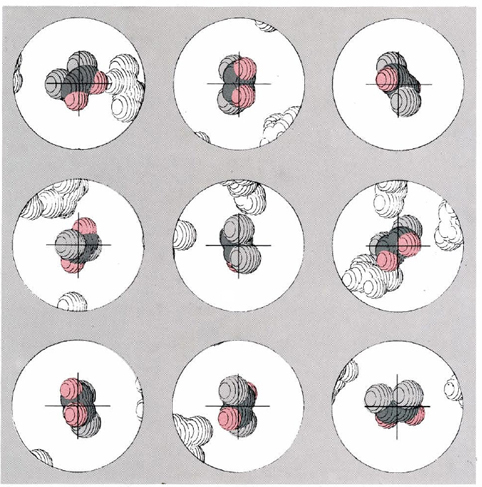
Figure \(\PageIndex{1}\) gives a computer simulation of this dynamic view of equilibrium for the cis-trans isomerization equilibrium of difluoroethene at 623 K. Suppose that it were possible to color one of the molecules in the equilibrium mixture and to photograph it at regular intervals thereafter under a high-power microscope. The figure shows the kind of results we could expect. In each “photograph” the molecule appears at a different orientation― between photos it has been bounced around quite a bit by collisions with other molecules. A careful inspection reveals a more important fact. Three of the nine photographs show the screened molecule in the trans conformation, while in the other six the molecule has the cis conformation. If we went on taking a large number of photographs of this molecule, we would find on the average that this ratio would be preserved. On the average one-third of the photographs would show the trans conformation, while the other two-thirds would show the cis form. The situation is much as though we had a conventional six-sided cubic die with the word trans printed on two sides and the word cis printed on the other four. If we roll this die a sufficient number of times, it will come up cis twice as often as trans.
We can now begin to see why it is that the equilibrium constant for this reaction is 0.5 at 623 K. Not only the screened molecule, but every other molecule in the equilibrium mixture as well, spends one-third of its time in the trans conformation and two-thirds in the cis conformation. At any given time, therefore, we will find a mixture in which one-third of the molecules are trans while the other two-thirds are cis. The ratio of trans to cis will be 1:2, or 0.5, as found experimentally.
Such an explanation is still not the whole story. We still need to explain why the dice are loaded against the trans conformation of a molecule of difluoroethene. Why is it that this isomer is less likely to occur in the constant reshuffle between the two conformations caused by the continual random collisions of molecules with each other in the equilibrium mixture? The reason is that the trans isomer is slightly higher in energy than the cis form. The enthalpy change ΔHm for the reaction
\[cis-\text{C}_2\text{H}_2\text{F}_2 \rightarrow trans-\text{C}_2\text{H}_2\text{F}_2 \nonumber \]
has the small, but nevertheless positive, value of +3.88 kJ mol–1.
In any collection of molecules, energy is constantly being transferred from one molecule to another as they collide. In this continual interchange of energy, inevitably some molecules acquire more kinetic or potential energy than their fellow molecules. However, when considering the distribution of kinetic energy, the probability of a molecule’s acquiring a given energy depends on the magnitude of that energy. The higher the energy, the less likely it is to occur. In the constant reshuffle of energies, molecules which are even slightly higher in energy than their fellows occur slightly less often. In the case under consideration, since a molecule of trans-difluoroethene is 3.88 kJ mol–1 higher in energy than the cis form, it will occur less often than the cis form in an equilibrium mixture in which each molecule is constantly flipping back and forth between the two forms. In other words, the die is loaded against the trans configuration because it is higher in energy.
We can now also understand why the position of equilibrium for this reaction varies with temperature. At a very low temperature it will be a rare occurrence for a molecule to acquire the extra 3.88 kJ mol–1 needed if it is to have the trans configuration. Accordingly, we expect the equilibrium mixture to contain many fewer trans molecules than cis molecules and the equilibrium constant
\[K_{c}=\frac{\text{ }\!\![\!\!\text{ }trans\text{-C}_{\text{2}}\text{H}_{\text{2}}\text{F}_{\text{2}}\text{ }\!\!]\!\!\text{ }}{\text{ }\!\![\!\!\text{ }cis\text{-C}_{\text{2}}\text{H}_{\text{2}}\text{F}_{\text{2}}\text{ }\!\!]\!\!\text{ }} \nonumber \]
to be quite small. Indeed, if it were possible to take the system down to absolute zero, no trans molecules would be possible and the value of Kc would be zero. As the temperature is increased, the probability of a molecule acquiring enough energy to assume the trans configuration increases, and increases along with it. Kc cannot increase indefinitely, though.
If the temperature is high enough, the energy difference between the cis and trans configurations becomes insignificant compared with the average kinetic energy of a molecule. Both forms will then be almost equally probable, and the value of Kc will be very slightly less than 1.
Very few chemical equilibria are as simple as the cis-trans isomerism of difluoroethene. In almost all other cases the position of equilibrium is governed not only by the energy difference between reactants and products but also by a probability factor which is independent of the energy. A simple example of such a probability factor is provided by the equilibrium between the ring and chain forms of 1,4-butanediol. The projection formula for this alcohol is
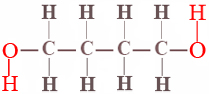
When a dilute solution (about 0.04 M) of this compound is prepared in carbon tetrachloride, the two ends of the molecule hydrogen-bond together to form a ring containing seven atoms, and an equilibrium between the ring form and the chain form is set up:
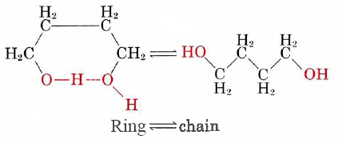
At 70°C (343 K) the equilibrium constant for this reaction is found by experiment to be
\[K_{c}=\frac{\text{ }\!\![\!\!\text{ chain }\!\!]\!\!\text{ }}{\text{ }\!\![\!\!\text{ ring }\!\!]\!\!\text{ }}=\text{1}\text{.22} \nonumber \]
So that there are about 22 percent more chain molecules than ring molecules in the equilibrium mixture at this temperature. This is contrary to what one would expect if energy were the only factor involved in determining the position of equilibrium. The chain form of the molecule is obviously higher in energy than the ring form, since energy must be supplied in order to break the hydrogen bond. Indeed ΔHm for Eq. (1) is found to be +13.5 kJ mol–1. On the basis of our previous argument, if the chain form is higher in energy, it should be less probable than the ring form and Kc should be less than 1. The experimental fact that Kc is greater than 1 means that there is some other factor making the chain form more probable than would be the case if energy alone were responsible.
In order to see what this other factor is, let us suppose that we can somehow investigate our system at a temperature which is so high that the energy difference between the ring and the chain form is insignificant. (In practice, the carbon tetrachloride solvent would boil off long before this temperature was obtained.) At such a temperature, if the energy difference between the two forms were the only factor determining their relative probability, we would expect the ring and chain forms (seen below) to be equally probable. It is easy to see, though, why this would not actually be the case.
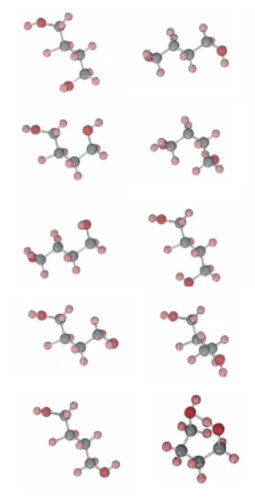
The chain form of 1,4-butanediol is a very flexible molecule because of the free rotation which is possible around the three carbon-carbon bonds and the two carbon-oxygen bonds. As it collides with its fellow molecules, it can adopt a very large number of different conformations. The figure below illustrates some of these conformations, selected at random by a computer. Again we can take these as representing a series of photographs of the same molecule taken at regular intervals, say every 5 min. For the sake of clarity, though, we have kept the position of two of the carbon atoms the same for each photograph. In actual fact the molecule would be rotating as well as flexing, and the orientation of the bond joining these two carbon atoms would be continually changing. We should also remember that the molecule has undergone very many collisions between successive photographs.
Figure \(\PageIndex{2}\) The chain form of butanediol. Because various segments of the molecule are free to rotate about carbon-carbon and carbon-oxygen bonds, the molecule can adopt a very large number of conformations. A random selection of nine of these is shown. Note that in none of these are the two oxygen atoms close enough to hydrogen bond together and form a ring. The ring form of butanediol. is at the bottom right. The two oxygen atoms at the top of the ring are hydrogen bonded together. From a strictly geometrical point of view this is a rather improbable conformation for the molecule. It is only because of the lowering in energy caused by the formation of a hydrogen bond that this ring form turns out to be slightly more probable in the equilibrium mixture than the chain form at low temperatures.
The important thing to notice about this random selection of nine conformations shown in Figure \(\PageIndex{2}\) is that in none of them are the two oxygen atoms close enough to allow the formation of a hydrogen bond. At this high temperature, because of the large number of ways in which a butanediol molecule can arrange itself in space, it will only occasionally adopt a ring conformation like that shown in Figure \(\PageIndex{3}\) in which the two oxygen atoms are close enough to hydrogen bond to each other. In the equilibrium mixture at high temperature, therefore, there will be many more chain molecules than ring molecules and Kc will be much larger than 1.
This situation begins to change as the temperature is reduced. With decreasing temperature, a smaller and smaller fraction of the molecules will have enough energy to break open a hydrogen bond. In consequence the ring form will become more probable. Once having formed, a ring will be able to survive quite a few collisions with other molecules before it is broken open again. Indeed, if we could reduce the temperature of our system close to absolute zero without the solvent freezing, then we would find that virtually all the butanediol molecules were in the ring form. Once formed, a ring would almost never experience a collision which was sufficiently energetic to break it open. At such a low temperature the value of Kc would be very close to zero.
The two equilibria we have just described have both been very simple examples, especially since they each involved only one reactant and one product. Nevertheless the principles we have discovered in discussing them apply to all chemical equilibria. We can always interpret the equilibrium constant of a chemical reaction as the product of two factors, each of which has a meaning on the microscopic level:
K = energy factor × probability factor (2)
The energy factor takes account of the fact that either the products or the reactants are higher in energy and hence less probable in the constant reshuffling of energy that goes on between molecules. The probability factor takes account of the fact that even if there were no energy difference between products and reactants, one or the other would still be more probable. This greater probability arises because of the larger number of ways in which the products (or reactants) can be realized on the molecular level.
In general the energy factor has the greatest effect on the value of the equilibrium constant at low temperatures. The lower the temperature, the very much lower the probability of a high-energy species occurring by chance in the constant energy reshuffle. At higher temperatures the effect of the energy factor becomes less pronounced and the probability factor becomes more important. If the temperature can be raised high enough, the probability factor eventually predominates.


