3.8.2: Environment- Gas
- Page ID
- 50736
You may have noticed "E85" gasoline selling for $2.39/gallon for FlexFuel vehicles while regular gas was selling for $2.79. Is E85 use advantageous if you have a FlexFuel vehicle capable of using either E85 (85% ethanol) or regular gas? Note that many states sell regular gas that is E10 (10% ethanol) for standard (non-FlexFuel) vehicles.
|
85% Ethanol at a modern pump |
The model T was first designed to run on ethanol[1] |
There are really (at least) two questions here:
1. Is it a good deal for the consumer (is energy from ethanol economical)?
2. Is it a good deal for the environment (is the Energy Balance favorable)?
The Energy Balance
The energy balance is the ratio of the energy produced by 1 kg of the fuel (i.e. ethanol), to the energy necessary to produce it (cultivation of plants, fermentation, transportation, irrigation, etc.). The energy balance for ethanol in the US is only 1.3 to 1.6 (we get 1.3-1.6 J out for 1 J energy input), while in Brazil it's 8.3 to 10.2. [2][3]
The energy balance for oil is about 5: Today, about 5 barrels of oil extracted for every 1 barrel of oil is consumed in the process (a century ago, when oil was more plentiful the ratio was 50:1).[4]
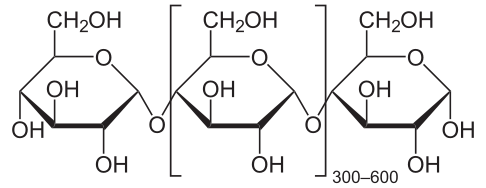
The reason for the poor energy balance for fuel ethanol in the US is that we use corn. We extract the cornstarch, and then hydrolyze it at high temperatures (over 90 oC and ferment the resulting sugars to give the ethanol (simultaneous saccharification and fermentation, SSF). More energy efficient processes are being developed. [5] Starch is a polymer of glucose composed of amylose (shown below) and amylopectin, a similar polymer with more branching. The chemical reactions that occur are first, hydrolysis of starches to maltose (C12H22O11):
-
- [C6H10O5]n + n/2 H2O → n/2 C12H22O11 (1)
 |
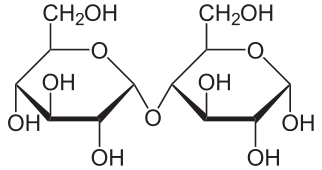 |
| Amylose | Maltose |
The complex sugar maltose is further hydrolyzed (sometimes in the same step) to glucose (C6H12O6):
-
- C12H22O11 + H2O → 2 C6H12O6 (2)
Finally, during ethanol fermentation, glucose is decomposed into ethanol (C2H5OH) and carbon dioxide.
-
- C6H12O6 → 2 C2H5OH + 2 CO2 + heat (3)
Switchgrass requires similar processing, but has the potential for a higher energy balance. In Brazil, sugarcane is used in ethanol production, eliminating the high energy cost reaction (1), because sugarcane produces sucrose, a sugar similar to maltose. In all cases, a large energy expenditure is necessary to separate the ethanol from the water in which the reactions take place, and other impurities.
 |
← Switchgrass |
 Corn |
But even in Brazil, rising sugar costs led to a rebound in reliance on petroleum, and E100 capable vehicles declined sharply in the late 1980s[6]. Nonetheless, the existence of ethanol pumps at a large percentage of gas stations has helped sustain the use of other blends. Clearly, the economics and history of fuel use should be studied carefully when investing in future fuel development.
The Cost Advantage
So which is a better deal: filling your 10-gallon tank with E85 costing $2.69/gallon or with gasoline costing $2.99/gallon?[7].
Energy changes which accompany chemical reactions are almost always expressed by thermochemical equations. For example, during combustion ethanol reacts with oxygen to produce carbon dioxide, water vapor, and heat according to the thermochemical equation:
-
- C2H5OH + 3 O2 → 2 CO2 + 3 H2O (l) (4) ΔHm = -1367 kJ[8]
The quantity ΔHm is the enthalpy change for the reaction equation as written. In this context the symbol Δ (delta) signifies change in” while H is the symbol for the quantity being changed, namely the enthalpy. We will deal with the enthalpy in some detail in Chap. 15. For the moment we can think of it as a property of matter which increases when matter absorbs energy and decreases when matter releases energy. Here the ΔHm (delta H subscript m) tells us whether heat energy is released or absorbed when the reaction occurs and also enables us to find the actual quantity of energy involved. By convention, if ΔHm is positive, heat is absorbed by the reaction; i.e., it is endothermic. More commonly, ΔHm is negative as in Eq. (3), indicating that heat energy is released rather than absorbed by the reaction, and that the reaction is exothermic. This convention as to whether ΔHm is positive or negative looks at the heat change in terms of the matter actually involved in the reaction rather than its surroundings. In the reaction in Eq. (4), stronger bonds have formed, leading to a decrease in potential energy, and it is this decrease which is indicated by a negative value of ΔHm.
It is important to notice that the quantity of heat released or absorbed by a reaction is proportional to the amount of each substance consumed or produced by the reaction. Thus Eq. (4) tells us that 1367 kJ of heat energy is given off for every mole of C2H5OH which is consumed. Alternatively, it tells us that 1367 kJ is released for every 3 moles of H2O produced, or every 2 mol of carbon dioxide produced, or every 3 mol of oxygen consumed. Seen in this way, ΔHm is a conversion factor enabling us to calculate the heat absorbed when a given amount of substance is consumed or produced. If q is the quantity of heat absorbed and n is the amount of substance involved, then
\(\Delta H_{\text{m}}=\frac{q}{n}\) (5) Equation (4) represents the standard heat of combustion, which is related to the "higher heating value" of a fuel.[9] Because liquid water is produced in Equation (4) and the heat (1367 kJ/mol) is given for a theoretical reaction occurring at 25 oC, it is only an approximation of the heat produced in an actual combustion, where the reaction takes place at a high temperature and produces water vapor. A better estimate may be the Lower Heating Value (LHV) which is adjusted by adding the heat of vaporization of water, and heat required to raise the temperature of reactants to the combustion temperature and products to 150 oC (an arbitrarily chosen standard).[10][11] We'll use the LHV for ethanol, -1330 kJ/mol,[12] and abbreviate ethanol (C2H5OH) as EtOH to calculate the heat in 1 gallon of ethanol:
\(V_{\text{EtOH}}~\xrightarrow{M}~m_{\text{EtOH}}\text{ }\xrightarrow{M}\text{ }n_{\text{EtOH}}~\xrightarrow{\Delta H_{m}}~q\)
so that
\(q=\text {1 gallon EtOH} ~\times~\frac{\text{3.79 L}}{\text{1 gallon}} ~\times~\frac{\text{1000 mL}}{\text{1 L}} ~\times~\frac{\text{0.789 g}}{\text{mL}} ~\times~\frac{\text{1 mol EtOH}}{\text{46.07 g EtOH}} ~\times~\frac{-\text{1330 kJ}}{\text{mol EtOH}} \)
\(=-86~330\text{ kJ}=-\text{86}\text{.33 MJ (estimate)}\)
We can calculate the energy value for octane, which represents gasoline fairly well, in a similar way. The thermochemical equation for the combustion of octane (C8H18) is:
C8H18 + 25/2 O2 → 8 CO2 + 9 H2O (l) (6) ΔH ~ -5430 kJ/mol[13]
Again, we'll use the LHV for octane (-5064 kJ/mol[14]) in our calculation:
\(q=\text {1 gallon octane} ~\times~\frac{\text{3.79 L}}{\text{1 gallon}} ~\times~\frac{\text{1000 mL}}{\text{1 L}} ~\times~\frac{\text{0.737 g}}{\text{mL}} ~\times~\frac{\text{1 mol octane}}{\text{114.23 g octane}} ~\times~\frac{\text{-5 064 kJ}}{\text{mol octane}} \)
\(=-123~800\text{ kJ}=-\text{123}\text{.80 MJ (estimate)}\)
So 1 gallon of gasoline has (123,800 / 86,330) or 1.4 times as much heating value, but costs only $2.79 / $2.39 or 1.2 times as much. It's the better buy. If the Energy Balance may only be about 1.3 in the US, it actually is a net loss to burn ethanol, at least at the current price and availability of petroleum. As the Energy Balance and availability of petroleum decreases, we had better develop more energy efficient means of ethanol production.
Indeed, based on EPA tests for all 2006 E85 models, the average fuel economy for E85 vehicles was 25.56% lower than unleaded gasoline.[15][16]
The Lower Heat Value (LHV)
It is important to realize that the value of ΔHm given in thermochemical equations like (4) or (6) depends on the physical state of both the reactants and the products. Thus, if water were obtained as a gas instead of a liquid in the reaction in Eq. (4), the value of ΔHm would be different from -1367 kJ. It is also necessary to specify both the temperature and pressure since the value of ΔHm depends very slightly on these variables. If these are not specified [as in Eq. (3)] they usually refer to 25°C and to normal atmospheric pressure.
Two more characteristics of thermochemical equations arise from the law of conservation of energy. The first is that writing an equation in the reverse direction changes the sign of the enthalpy change. For example,
H2O(l) → H2O(g) ΔHm = 44 kJ (7a) tells us that when a mole of liquid water vaporizes, 44 kJ of heat is absorbed. This corresponds to the fact that heat is absorbed from your skin when perspiration evaporates, and you cool off. Condensation of 1 mol of water vapor, on the other hand, gives off exactly the same quantity of heat. H2O(g) → H2O(l) ΔHm = –44 kJ (7b) To see why this must be true, suppose that ΔHm [Eq. (7a)] = 44 kJ while ΔHm [Eq. (7b)] = –50.0 kJ. If we took 1 mol of liquid water and allowed it to evaporate, 44 kJ would be absorbed. We could then condense the water vapor, and 50.0 kJ would be given off. We could again have 1 mol of liquid water at 25°C but we would also have 6 kJ of heat which had been created from nowhere! This would violate the law of conservation of energy. The only way the problem can he avoided is for ΔHm of the reverse reaction to be equal in magnitude but opposite in sign from ΔHm of the forward reaction. That is,
ΔHm forward = –ΔHm reverse
Since Reaction (4) produces 3 mol of H2O(l), it would produce 3 mol x 44 kJ/mol = 132 kJ less energy if the water were produced as the vapor, because the heat released in condensation to the liquid would not be included. The enthalpy change would then be -1367 + 132 kJ or -1235 kJ. This is still different from the LHV because of the heat required to change the temperature of the reactants and products from the standard temperature (25 oC) to the combustion temperature.
FlexFuel Facts
In 2007, only 3.3% of American cars were FlexFuel and only 1% of the filling stations provided FlexFuel, but the percentage has been increasing rapidly. World ethanol production for transport fuel tripled between 2000 and 2007 from 17 billion to more than 52 billion litres, with 89% produced in Brazil and the US.[17] The price differential shows large changes (it was about 30% in 2007).[18] The National Alcohol Program in Brazil, a world leader in using ethanol fuel, mandated decreased reliance on petroleum after the first oil crisis in 1973, and by 1979 several automakers provided cars that ran on pure ethanol (E100). After reaching more than 4 million cars and light trucks running on pure ethanol by the late 1980s,[3] the use of E100-only vehicles sharply declined after increases in sugar prices produced shortages of ethanol fuel. The emphasis has been on E85 (85% ethanol) vehicles in the US, because engines won't start reliably on E100 below about 60 oF. Even E85 cannot be used below about 30 oF, and in northern states E70 is delivered by E85 pumps without changing the label.[19]
References
- en.Wikipedia.org/wiki/Flex_fuel
- en.Wikipedia.org/wiki/Ethanol_fuel#Comparison%20of%20Brazil%20and%20the%20U.S.
- en.Wikipedia.org/wiki/Ethanol_fuel_energy_balance
- en.Wikipedia.org/wiki/Net_energy_gain
- ddr.nal.usda.gov/bitstream/10...ND43897867.pdf
- en.Wikipedia.org/wiki/Flex_fuel
- http://www.ched-ccce.org/confchem/2010/Spring2010/P7-Cummings.html
- webbook.nist.gov/cgi/cbook.cg...ermo-Condensed
- en.Wikipedia.org/wiki/Higher_heating_value
- en.Wikipedia.org/wiki/Lower_heating_value
- en.Wikipedia.org/wiki/Heat_of_combustion
- en.Wikipedia.org/wiki/Lower_heating_value
- http://webbook.nist.gov/cgi/cbook.cg...ermo-Condensed
- en.Wikipedia.org/wiki/Lower_heating_value
- en.Wikipedia.org/wiki/Flex_fuel
- Goettemoeller, Jeffrey; Adrian Goettemoeller (2007). Sustainable Ethanol: Biofuels, Biorefineries, Cellulosic Biomass, Flex-Fuel Vehicles, and Sustainable Farming for Energy Independence. Prairie Oak Publishing, Maryville, Missouri. pp. 56–61. ISBN 978-0-9786293-0-4.
- en.Wikipedia.org/wiki/Ethanol_fuel
- en.Wikipedia.org/wiki/Flex_fuel
- en.Wikipedia.org/wiki/Ethanol_fuel





