16.2: Galvanic cells and Electrodes

It is physically impossible to measure the potential difference between a piece of metal and the solution in which it is immersed. We can, however, measure the difference between the potentials of two electrodes that dip into the same solution, or more usefully, are in two different solutions. In the latter case, each electrode-solution pair constitutes an oxidation-reduction half cell, and we are measuring the sum of the two half-cell potentials.

This arrangement is called a galvanic cell. A typical cell might consist of two pieces of metal, one zinc and the other copper, each immersed each in a solution containing a dissolved salt of the corresponding metal. The two solutions are separated by a porous barrier that prevents them from rapidly mixing but allows ions to diffuse through.

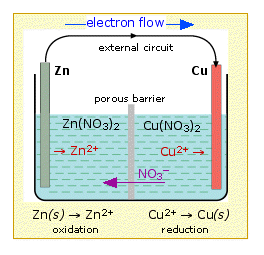
If we connect the zinc and copper by means of a metallic conductor, the excess electrons that remain when Zn²⁺ ions emerge from the zinc in the left cell would be able to flow through the external circuit and into the right electrode, where they could be delivered to the Cu²⁺ ions which become "discharged", that is, converted into Cu atoms at the surface of the copper electrode. The net reaction is the oxidation of zinc by copper(II) ions:

\[Zn_{(s)} + Cu^{2+} \rightarrow Zn^{2+} + Cu_{(s)}\]

but this time, the oxidation and reduction steps (half reactions) take place in separate locations:

left electrode:	Zn(s) → Zn^2^+ + 2e^–	oxidation
right electrode:	Cu^2^+ + 2e^–→ Cu(s)	reduction

Electrochemical cells allow measurement and control of a redox reaction

The reaction can be started and stopped by connecting or disconnecting the two electrodes. If we place a variable resistance in the circuit, we can even control the rate of the net cell reaction by simply turning a knob. By connecting a battery or other source of current to the two electrodes, we can force the reaction to proceed in its non-spontaneous, or reverse direction. By placing an ammeter in the external circuit, we can measure the amount of electric charge that passes through the electrodes, and thus the number of moles of reactants that get transformed into products in the cell reaction.

Electric charge q is measured in coulombs. The amount of charge carried by one mole of electrons is known as the Faraday, which we denote by F. Careful experiments have determined that 1 F = 96467 C. For most purposes, you can simply use 96,500 Coulombs as the value of the faraday. When we measure electric current, we are measuring the rate at which electric charge is transported through the circuit. A current of one ampere corresponds to the flow of one coulomb per second.

Charge Transport within the Cell

For the cell to operate, not only must there be an external electrical circuit between the two electrodes, but the two electrolytes (the solutions) must be in contact. The need for this can be understood by considering what would happen if the two solutions were physically separated. Positive charge (in the form of Zn²⁺) is added to the electrolyte in the left compartment, and removed (as Cu²⁺) from the right side, causing the solution in contact with the zinc to acquire a net positive charge, while a net negative charge would build up in the solution on the copper side of the cell. These violations of electroneutrality would make it more difficult (require more work) to introduce additional Zn²⁺ ions into the positively-charged electrolyte or for electrons to flow into right compartment where they are needed to reduce the Cu²⁺ ions, thus effectively stopping the reaction after only a chemically insignificant amount has taken place.

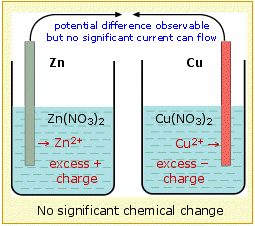
In order to sustain the cell reaction, the charge carried by the electrons through the external circuit must be accompanied by a compensating transport of ions between the two cells. This means that we must provide a path for ions to move directly from one cell to the other. This ionic transport involves not only the electroactive species Cu²⁺ and Zn²⁺, but also the counterions, which in this example are nitrate, NO₃^-. Thus an excess of Cu²⁺ in the left compartment could be alleviated by the drift of these ions into the right side, or equally well by diffusion of nitrate ions to the left. More detailed studies reveal that both processes occur, and that the relative amounts of charge carried through the solution by positive and negative ions depends on their relative mobilities, which express the velocity with which the ions are able to make their way through the solution. Since negative ions tend to be larger than positive ions, the latter tend to have higher mobilities and carry the larger fraction of charge.

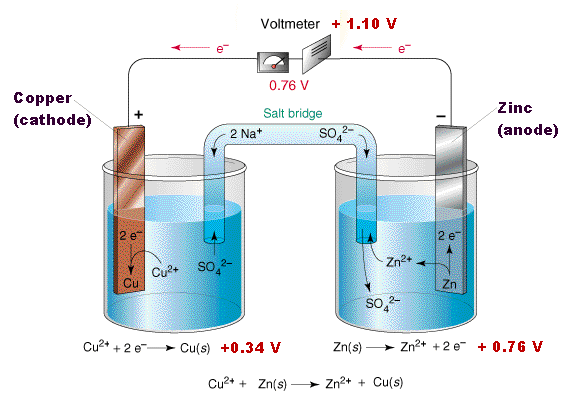
In the simplest cells, the barrier between the two solutions can be a porous membrane, but for precise measurements, a more complicated arrangement, known as a salt bridge, is used. The salt bridge consists of an intermediate compartment filled with a concentrated solution of KCl and fitted with porous barriers at each end. The purpose of the salt bridge is to minimize the natural potential difference, known as the junction potential, that develops (as mentioned in the previous section) when any two phases (such as the two solutions) are in contact. This potential difference would combine with the two half-cell potentials so as introduce a degree of uncertainty into any measurement of the cell potential. With the salt bridge, we have two liquid junction potentials instead of one, but they tend to cancel each other out.

Cell description conventions

In order to make it easier to describe a given electrochemical cell, a special symbolic notation has been adopted. In this notation the cell we described above would be

Zn(s) | Zn²⁺(aq) || Cu²⁺(aq) | Cu(s)

There are several other conventions relating to cell notation and nomenclature that you are expected to know:

• The anode is where oxidation occurs, and the cathode is the site of reduction. In an actual cell, the identity of the electrodes depends on the direction in which the net cell reaction is occurring.
• If electrons flow from the left electrode to the right electrode (as depicted in the above cell notation) when the cell operates in its spontaneous direction, the potential of the right electrode will be higher than that of the left, and the cell potential will be positive.
• "Conventional current flow" is from positive to negative, which is opposite to the direction of the electron flow. This means that if the electrons are flowing from the left electrode to the right, a galvanometer placed in the external circuit would indicate a current flow from right to left.

Electrodes and Electrode Reactions

An electrode reaction refers to the net oxidation or reduction process that takes place at an electrode. This reaction may take place in a single electron-transfer step, or as a succession of two or more steps. The substances that receive and lose electrons are called the electroactive species.

Fig. 4: Electron transfer at an anode

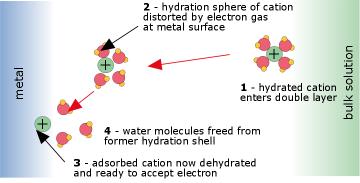
This process takes place within the very thin interfacial region at the electrode surface, and involves quantum-mechanical tunneling of electrons between the electrode and the electroactive species. The work required to displace the H₂O molecules in the hydration spheres of the ions constitutes part of the activation energy of the process.

In the example of the Zn/Cu cell we have been using, the electrode reaction involves a metal and its hydrated cation; we call such electrodes metal-metal ion electrodes. There are a number of other kinds of electrodes which are widely encountered in electrochemistry and analytical chemistry.

Ion-ion Electrodes

Many electrode reactions involve only ionic species, such as \(Fe^{2+}\) and \(Fe^{3+}\). If neither of the electroactive species is a metal, some other metal must serve as a conduit for the supply or removal of electrons from the system. In order to avoid complications that would arise from electrode reactions involving this metal, a relatively inert substance such as platinum is commonly used. Such a half cell would be represented as

Pt(s) | Fe³⁺(aq), Fe²⁺(aq) || ...

and the half-cell reaction would be

\[Fe^{2+}(aq) \rightarrow Fe^{3+} (aq) + e^-\]

The reaction occurs at the surface of the electrode (Fig 4 above). The electroactive ion diffuses to the electrode surface and adsorbs (attaches) to it by van der Waals and Coulombic forces. In doing so, the waters of hydration that are normally attached to any ionic species must be displaced. This process is always endothermic, sometimes to such an extent that only a small fraction of the ions be able to contact the surface closely enough to undergo electron transfer, and the reaction will be slow. The actual electron-transfer occurs by quantum-mechanical tunnelling.

Gas Electrodes

Some electrode reactions involve a gaseous species such as \(H_2\), \(O_2\), or \(Cl_2\). Such reactions must also be carried out on the surface of an electrochemically inert conductor such as platinum. A typical reaction of considerable commercial importance is

\[Cl^-(aq) \rightarrow ½ Cl_2(g) + e^- \]

Similar reactions involving the oxidation of \(Br_2\) or \(I_2\) also take place at platinum surfaces.

Insoluble–salt Electrodes

A typical electrode of this kind consists of a silver wire covered with a thin coating of silver chloride, which is insoluble in water. The electrode reaction consists in the oxidation and reduction of the silver:

\[AgCl(s) + e^– → Ag(s) + Cl^–(aq)\]

The half cell would be represented as

\[ ... || Cl^– (aq) | AgCl (s) | Ag (s)\]

Although the usefulness of such an electrode may not be immediately apparent, this kind of electrode finds very wide application in electrochemical measurements, as we shall see later.

Reference Electrodes

In most electrochemical experiments our interest is concentrated on only one of the electrode reactions. Since all measurements must be on a complete cell involving two electrode systems, it is common practice to employ a reference electrode as the other half of the cell. The major requirements of a reference electrode are that it be easy to prepare and maintain, and that its potential be stable. The last requirement essentially means that the concentration of any ionic species involved in the electrode reaction must be held at a fixed value. The most common way of accomplishing this is to use an electrode reaction involving a saturated solution of an insoluble salt of the ion. One such system, the silver-silver chloride electrode has already been mentioned:

\[Ag | AgCl(s) | Cl^–(aq) || ...\]

\[Ag(s) + Cl^–(aq) →AgCl(s) + e^–\]

This electrode usually takes the form of a piece of silver wire coated with AgCl. The coating is done by making the silver the anode in an electrolytic cell containing HCl; the Ag⁺ ions combine with Cl^– ions as fast as they are formed at the silver surface.

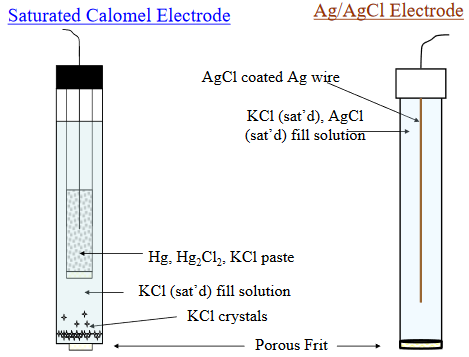
The other common reference electrode is the calomel electrode; calomel is the common name for mercury(I) chloride. Such a half cell would be represented as

\[Hg | Hg^{2+}(aq) | KCl || ...\]

and the half-cell reaction would be

\[Hg(l) + Cl^– → ½ HgCl2(s) + e^–\]

The potentials of both of these electrodes have been very accurately determined against the hydrogen electrode. The latter is seldom used in routine electrochemical measurements because it is more difficult to prepare; the platinum surface has to be specially treated by preliminary electrolysis. Also, there is need for a supply of hydrogen gas which makes it somewhat cumbersome and hazardous.

Summary and additional notes

Make sure you thoroughly understand the following essential ideas which have been presented above. It is especially important that you know the precise meanings of all the highlighted terms in the context of this topic.

• A galvanic cell (sometimes more appropriately called a voltaic cell) consists of two half-cells joined by a salt bridge or some other path that allows ions to pass between the two sides in order to maintain electroneutrality.
• The conventional way of representing an electrochemical cell of any kind is to write the oxidation half reaction on the left and the reduction on the right. Thus for the reaction

Zn(s) + Cu²⁺ → Zn²⁺ + Cu(s)

we write

Zn(s) | Zn²⁺(aq) || Cu²⁺(aq) | Cu(s)

in which the single vertical bars represent phase boundaries. The double bar denotes a liquid-liquid boundary which in laboratory cells consists of a salt bridge or in ion-permeable barrier. If the net cell reaction were written in reverse, the cell notation would become

Cu(s) | Cu²⁺(aq) || Zn ²⁺(aq) | Zn (s)

Remember: the Reduction process is always shown on the Right.

at the electrode surface. The energy required to displace water molecules from the hydration shell of an ion as it approaches the electrode surface constitutes an activation energy which can slow down the process. Even larger activation energies (and slower reactions) occur when a molecule such as O₂ is formed or consumed.