8.2.2D: Solutions of Solid Solutes in Liquid Solvents
- Page ID
- 78405
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Make sure you thoroughly understand the following essential ideas:
- A key to understanding the solubility of ionic solids in water are the concepts of lattice energy and hydration energy. Explain the meaning of these terms, and sketch out a diagram that shows how these are related to the "heat of solution".
Molecular Solids in Liquid Solvents
The stronger intermolecular forces in solids require more input of energy to disperse the molecular units into a liquid solution, but there is also a considerable increase in entropy that can more than compensate if the intermolecular forces are not too strong, and if the solvent has no strong hydrogen bonds that must be broken in order to introduce the solute into the liquid.
| solvent → | non polar liquid | polar liquid |
|---|---|---|
| energy to disperse solute | moderate | moderate |
| energy to introduce into solvent | small | moderate |
| increase in entropy | moderate | moderate |
| miscibility | moderate | small |
For example, at 25° C and 1 atm pressure, 20 g of iodine crystals will dissolve in 100 ml of ethyl alcohol, but the same quantity of water will dissolve only 0.30 g of iodine. As the molecular weight of the solid increases, the intermolecular forces holding the solid together also increase, and solubilities tend to fall off; thus the solid linear hydrocarbons CH3(CH2)nCH3 (n > 20) show diminishing solubilities in hydrocarbon liquids.
Ionic Solids in Liquid Solvents
Since the Coulombic forces that bind ions and highly polar molecules into solids are quite strong, we might expect these solids to be insoluble in just about any solvent. Ionic solids are insoluble in most non-aqueous solvents, but the high solubility of some (including NaCl) in water suggests the need for some further explanation.
| solvent → | non polar | polar (water) |
|---|---|---|
| energy to disperse solute | large | large (endothermic) |
| energy to introduce into liquid | small | highly negative (exothermic) |
| increase in entropy | moderate | moderate to slightly negative |
| miscibility | very small | small to large |
The key factor here turns out to be the interaction of the ions with the solvent. The electrically-charged ions exert a strong coulombic attraction on the end of the water molecule that has the opposite partial charge.
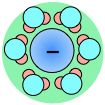
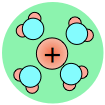
As a consequence, ions in solution are always hydrated; that is, they are quite tightly bound to water molecules through ion-dipole interaction. The number of water molecules contained in the primary hydration shell varies with the radius and charge of the ion.
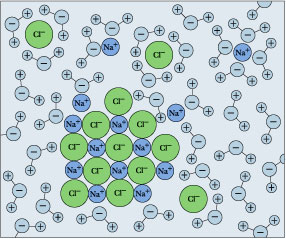
Figure \(\PageIndex{1}\): Hydration shells around some ions in a sodium chloride solution. The average time an ion spends in a shell is about 2-4 nanoseconds. But this is about two orders of magnitude longer than the lifetime of an individual \(H_2O–H_2O\) hydrogen bond.
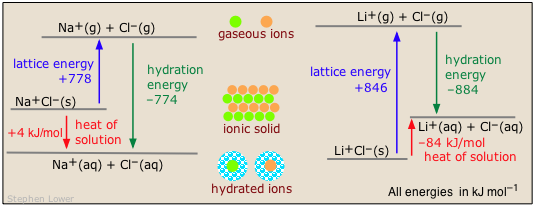
Lattice and Hydration Energies
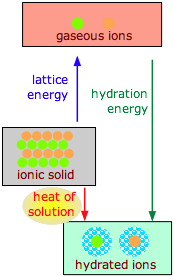
The dissolution of an ionic solid \(M\)X in water can be thought of as a sequence of two (hypothetical) steps:
\[MX(s) \rightarrow M^+(g) + X^–(g) \]
\[M^+(g) + X^–(g) + H_2O(l) \rightarrow M^+(aq) + X–(aq)\]
The enthalpy difference of the first step is the lattice energy and is always positive; the enthalpy difference of the second step is the hydration energy and is always negative)
- The first reaction is always endothermic; it takes a lot of work to break up an ionic crystal lattice (Table \(\PageIndex{1}\)).
- The hydration step is always exothermic as H2O molecules are attracted into the electrostatic field of the ion (Table \(\PageIndex{2}\)).
- The heat (enthalpy) of solution is the sum of the lattice and hydration energies, and can have either sign.
| H+(g) | –1075 | F–(g) | –503 |
| Li+(g) | –515 | Cl–(g) | –369 |
| Na+(g) | –405 | Br–(g) | –336 |
| K+(g) | –321 | I–(g) | –398 |
| Mg2+(g) | –1922 | OH–(g) | –460 |
| Ca2+(g) | –1592 | NO3– | –328 |
| Sr2+(g) | –1445 | SO42– | –1145 |
Single-ion hydration energies (Table \(\PageIndex{1}\)) cannot be observed directly, but are obtained from the differences in hydration energies of salts having the given ion in common. When you encounter tables such as the above in which numeric values are related to different elements, you should always stop and see if you can make sense of any obvious trends. In this case, the things to look for are the size and charge of the ions as they would affect the electrostatic interaction between two ions or between an ion and a [polar] water molecule.
| F– | Cl– | Br– | I– | |
|---|---|---|---|---|
| Li+ | +1031 | +848 | +803 | +759 |
| Na+ | +918 | +780 | +742 | +705 |
| K+ | +817 | +711 | +679 | +651 |
| Mg2+ | +2957 | +2526 | +2440 | +2327 |
| Ca2+ | +2630 | +2258 | +2176 | +2074 |
| Sr2+ | +2492 | +2156 | +2075 | +1963 |
Lattice energies are not measured directly, but are estimates based on electrostatic calculations which are reliable only for simple salts. Enthalpies of solution are observable either directly or (for sparingly soluble salts,) indirectly. Hydration energies are not measurable; they are estimated as the sum the other two quantities. It follows that any uncertainty in the lattice energies is reflected in those of the hydration energies. For this reason, tabulated values of the latter will vary depending on the source.
When calcium chloride, CaCl2, is dissolved in water, will the temperature immediately after mixing rise or fall?
Solution:
Estimate the heat of solution of CaCl2.
- lattice energy of solid CaCl2: +2258 kJ mol–1
- hydration energy of the three gaseous ions: (–1562 –381 – 381) = –2324 kJ mol–1
- heat of solution:
(2258 – 2324) kJ mol–1 = –66 kJ mol–1
Since the process is exothermic, this heat will be released to warm the solution.
As often happens for a quantity that is the sum of two large terms having opposite signs, the overall dissolution process can come out as either endothermic or exothermic, and examples of both kinds are common.
|
substance →
|
LiF | NaI | KBr | CsI | LiCl | NaCl | KCl | AgCl |
|---|---|---|---|---|---|---|---|---|
| lattice energy | 1021 | 682 | 669 | 586 | 846 | 778 | 707 | 910 |
| hydration energy | 1017 | 686 | 649 | 552 | 884 | 774 | 690 | 844 |
| enthalpy of solution | +3 | –4 | +20 | +34 | –38 | +4 | +17 | +66 |
Two common examples illustrate the contrast between exothermic and endothermic heats of solution of ionic solids:
Hydration Entropy can make a Difference!
Hydration shells around some ions in a sodium chloride solution. The average time an ion spends in a shell is about 2-4 nanoseconds. But this is about two orders of magnitude longer than the lifetime of an individual \(H_2O\)–\(H_2O\) hydrogen bond. The balance between the lattice energy and hydration energy is a major factor in determining the solubility of an ionic crystal in water, but there is another factor to consider as well. We generally assume that there is a rather large increase in the entropy when a solid is dispersed into the liquid phase. However, in the case of ionic solids, each ion ends up surrounded by a shell of oriented water molecules. These water molecules, being constrained within the hydration shell, are unable to participate in the spreading of thermal energy throughout the solution, and reduce the entropy. In some cases this effect predominates so that dissolution of the salt leads to a net decrease in entropy. Recall that any process in which the the entropy diminishes becomes less probable as the temperature increases; this explains why the solubilities of some salts decrease with temperature.


