4.1: Atoms, Elements, and the Nucleus
- Page ID
- 3602
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Make sure you thoroughly understand the following essential ideas:
- Give a chemical definition of element, and comment on the distinction between the terms atom and element.
- You should know the names and symbols of the more common elements, including those whose symbols are derived from their Latin names.
- Describe, in your own words, the Laws of Chemical Change: mass conservation, constant composition, and multiple proportions.
- Explain how these laws follow from Dalton's atomic theory.
- Describe Rutherford's alpha-ray scattering experiment and how it led to the present model of the atom.
- Define atomic number and mass number, and explain the relation between them.
- Define isotope and nuclide, and write the symbol for a nuclide of a given element with a given number of neutrons.
- Explain the purpose of a mass spectrometer and its general principle of operation.
- Describe the atomic weight scale.
- Find the molecular weight or formula weight from a chemical formula.
- Define the unified atomic mass unit, and write out the mass numbers of the proton, neutron, and electron.
The parallel concepts of the element and the atom constitute the very foundations of chemical science. As such, the concept of the element is a macroscopic one that relates to the world that we can observe with our senses. The atom is the microscopic realization of this concept; that is, it is the actual physical particle that is unique to each chemical element. Their very small size has long prevented atoms from being observable by direct means, so their existence was not universally accepted until the late 19th Century. The fact that we still hear the mention of the "atomic theory of matter" should not imply that there is now any doubt about the existence of atoms. Few theories in the history of science have been as thoroughly validated and are as well understood.

Although the word atom usually refers to a specific kind of particle (an "atom of magnesium", for example), our everyday use of element tends to be more general, referring not only to a substance composed of a particular type of atom ("bromine is one of the few elements that are liquids at room temperature"), but also to atoms in a collective sense ("magnesium is one of the elements having two electrons in its outer shell").
The underlying concept of atoms as the basic building blocks of matter has been around for a long time. As early as 600 BCE, the Gujarati (Indian) philosopher Acharya Kanad wrote that "Every object of creation is made of atoms which in turn connect with each other to form molecules". A couple of centuries later in 460 BCE, the Greek philosopher Democritus reasoned that if you keep breaking a piece of matter into smaller and smaller fragments, there will be some point at which the pieces cannot be made any smaller. He called these "basic matter particles"— in other words, atoms. But this was just philosophy; it would not become science until 1800 when John Dalton showed how the atomic concept followed naturally from the results of quantitative experiments based on weight measurements.
Elements
The element is the fundamental unit of chemical identity. The concept of the element is very ancient. It was developed in many different civilizations in an attempt to rationalize the variety of the world and to understand the nature of change, such as, change that occurs when a piece of wood rots, or is burnt to produce charcoal or ash. Most well known to us are the four elements "earth, air, fire and water" that were popularized by Greek philosophers (principally Empedocoles and Aristotle) in the period 500-400 BCE.
To these, Vedic (Hindu) philosophers of India added space, while the ancient Chinese concept of Wu Xing regarded earth, metal, wood, fire and water as fundamental. These basic elements were not generally considered to exist as the actual materials we know as earth, water, etc., but rather to represent the "principles" or essences that the elements conveyed to the various kinds of matter we encounter in the world.
Eventually, practical experience (largely connected with the extraction of metals from ores) and the beginnings of scientific experimentation in the 18th Century led to our modern concept of the chemical element. An element is a substance: the simplest form to which any other chemical substance can be reduced through appropriate thermal or chemical treatment. "Simplest", in the context of experimentation at the time, was defined in terms of weight; cinnabar (mercuric sulfide) can be broken down into two substances, mercury and sulfur, which themselves cannot be reduced to any lighter forms.

Although Lavoisier got many of these right, he did manage to include a few things that do not quite fit into our modern idea of what constitutes a chemical element. There are two such mistakes in the top section of the table that you should be able to identify even if your French is less than tip-top— can you find them?
Lavoisier's other misassignment of the elements in the bottom section was not really his fault. Chalk, magnesia, barytes, alumina and silica are highly stable oxygen-containing compounds; the high temperatures required to break them down could not be achieved in Lavoisier's time (magnesia is what fire brick is made of). The proper classification of these substances was delayed until further experimentation revealed their true nature. Ten of the chemical elements have been known since ancient times and five more were discovered through the 17th Century.
Some frequently-asked questions about elements
- How many elements are there? Ninety-two elements have been found in nature. Around 25 more have been made artificially, but all of these decay into lighter elements, with some of them disappearing in minutes or even seconds.
- Where do the elements come from? The present belief is that helium and a few other very light elements were formed within about three minutes of the "big bang", and that the next 23 elements (up through iron) are formed mostly by nuclear fusion processes within stars, in which lighter nuclei combine into successively heavier elements. Elements heavier than iron cannot be formed in this way, and are produced only during the catastrophic collapse of massive stars (supernovae explosions).
- How do the elements vary in abundance? Quite markedly, and very differently in different bodies in the cosmos. Most of the atoms in the universe still consist of hydrogen, with helium being a distant second. On Earth, oxygen, silicon, and aluminum are most abundant. These profiles serve as useful guides for constructing models for the formation of the earth and other planetary bodies. The system of element symbols we use today was established by the Swedish chemist Jons Jacob Berzelius in 1814. Prior to that time, graphical alchemical symbols were used, which were later modified and popularized by John Dalton. Fortunately for English speakers, the symbols of most of the elements serve as mnemonics for their names, but this is not true for the seven metals known from antiquity, whose symbols are derived from their Latin names. The other exception is tungsten (a name derived from Swedish), whose symbol W reflects the German name which is more widely used.
- How are the elements organized? Two general organizing principles developed in the 19th Century: one was based on the increasing relative weights (atomic weights) of the elements, yielding a list that begins this way:
H He Li Be B C N O F Ne Na Mg Al Si P S Cl Ar K Ca...
Atoms become real
Throughout most of history the idea that matter is composed of minute particles had languished as a philosophical abstraction known as atomism, and no clear relation between these "atoms" and the chemical "elements" had been established. This began to change in the early 1800's when the development of balances that permitted reasonably precise measurements of the weight changes associated with chemical reactions ushered in a new and fruitful era of experimental chemistry. This resulted in the recognition of several laws of chemical change that laid the groundwork for the atomic theory of matter.

Laws of Chemical Change
Recall that a "law", in the context of science, is just a relationship, discovered through experimentation, that is sufficiently well established to be regarded as beyond question for most practical purposes. Because it is the nature of scientists to question the "unquestionable", it occasionally happens that exceptions do arise, in which case the law must undergo appropriate modification.
Conservation of mass-energy is usually considered the most fundamental of law of nature. It is also a good example of a law that had to be modified; it was known simply as Conservation of Mass until Einstein showed that energy and mass are interchangeable. However, the older term is perfectly acceptable within the field of ordinary chemistry in which energy changes are too small to have a measurable effect on mass relations. Within the context of chemistry, conservation of mass can be thought of as "conservation of atoms". Chemical change just shuffles them around into new arrangements.
Mass conservation had special significance in understanding chemical changes involving gases, which were for some time not always regarded as real matter at all. (Owing to their very small densities, carrying out actual weight measurements on gases is quite difficult to do, and was far beyond the capabilities of the early experimenters.) Thus when magnesium metal is burned in air, the weight of the solid product always exceeds that of the original metal, implying that the process is one in which the metal combines with what might have been thought to be a "weightless" component of the air, which we now know to be oxygen.

More importantly, this experimental result tells us something very important about the mass of the oxygen atom relative to that of the magnesium atom.
The Law of Definite Proportions, also known as the law of constant composition, states that the proportion by weight of the element present in any pure substance is always the same. This enables us to generalize the relationship we illustrated above.
How many kilograms of metallic magnesium could theoretically be obtained by decomposing 0.400 kg of magnesium oxide into its elements?
Solution
The mass ratio of Mg to O in this compound is
\[\dfrac{1}{1.66} = 0.602 \nonumber\]
so 0.400 kg of the oxide contains
\[(0.400\; kg) \times 0.602 = 0.241\; \text{kg of Mg} \nonumber .\]
The fact that we are concerned with the reverse of the reaction cited above is irrelevant.
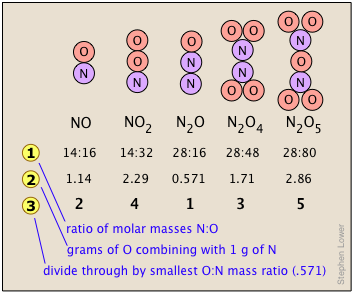
The Law of Multiple Proportions address the fact that Many combinations of elements can react to form more than one compound. In such cases, this law states that the weights of one element that combine with a fixed weight of another of these elements are integer multiples of one another. It's easy to say this, but please make sure that you understand how it works. Nitrogen forms a very large number of oxides, five of which are shown here.
- Line
 shows the ratio of the relative weights of the two elements in each compound. These ratios were calculated by simply taking the molar mass of each element, and multiplying by the number of atoms of that element per mole of the compound. Thus for NO2, we have (1 × 14) : (2 × 16) = 13:32. (These numbers were not known in the early days of Chemistry because atomic weights (i.e., molar masses) of most elements were not reliably known.)
shows the ratio of the relative weights of the two elements in each compound. These ratios were calculated by simply taking the molar mass of each element, and multiplying by the number of atoms of that element per mole of the compound. Thus for NO2, we have (1 × 14) : (2 × 16) = 13:32. (These numbers were not known in the early days of Chemistry because atomic weights (i.e., molar masses) of most elements were not reliably known.) - The numbers in Line
 are just the mass ratios of O:N, found by dividing the corresponding ratios in line 1. But someone who depends solely on experiment would work these out by finding the mass of O that combines with unit mass (1 g) of nitrogen.
are just the mass ratios of O:N, found by dividing the corresponding ratios in line 1. But someone who depends solely on experiment would work these out by finding the mass of O that combines with unit mass (1 g) of nitrogen. - Line is obtained by dividing the figures the previous line by the smallest O:N ratio in the line above, which is the one for N2O. Note that just as the law of multiple proportions says, the weight of oxygen that combines with unit weight of nitrogen work out to small integers.
- Of course we just as easily could have illustrated the law by considering the mass of nitrogen that combines with one gram of oxygen; it works both ways!
Nitrogen and hydrogen form many compounds, some of which involve other elements as well. The mass of hydrogen that combines with 1.00 g of nitrogen to form three of these compounds are: urea, 0.1428 g; ammonia, 0.0714 g; ammonium chloride, 0.2857 g. Show that this data is consistent with the Law of Multiple Proportions.
Solution
The "fixed weight" we are considering here is the nitrogen. Inspection of the numbers above shows that the ammonia contains the smallest weight ratio H:N = 0.0714, while the weight ratio of H:N in urea is twice this number, and that in ammonium chloride is four times 0.0714. Thus the H:N ratios are themselves stand in the ratio of 2:1:4, respectively, and the Law is confirmed.
Dalton's Interpretation Established Atomic Theory
The idea that matter is composed of tiny "atoms" of some kind had been around for at least 2000 years. Dalton's accomplishment was to identify atoms with actual chemical elements.

If Nobel prizes had existed in the early 1800's, the English school teacher/ meteorologist/ chemist John Dalton (1766-1844) would certainly have won one for showing how the experimental information available at that time, as embodied in the laws of chemical change that we have just described, are fully consistent with the hypothesis that atoms are the smallest units of chemical identity. These points of Dalton's atomic theory provided satisfactory explanations of all the laws of chemical change noted above:
Dalton's explanation of the Law of Conservation of Mass was that it is really a consequence of "conservation of atoms" which are presumed to be indestructible by chemical means. In chemical reactions, the atoms are simply rearranged, but never destroyed.
Dalton's Explanation of the law of constant composition was that if compounds are made up of definite numbers of atoms, each of which has its own characteristic mass, then the relative mass of each element in a compound must always be the same. Thus the elements must always be present in a pure sample of a compound in the same proportions by mass.
A given set of elements can usually form two or more compounds in which the numbers of atoms of some of the elements are different. Because these numbers must be integers (you can't have "half" an atom!), the mass of one element combined with a fixed mass of any other elements in any two such compounds can differ only by integer numbers. Thus, for the series of nitrogen-hydrogen compounds cited in the Problem Example above, we have the following relations:
| Compound | Formula | weight ratio H:N | ratio to 0.0714 |
|---|---|---|---|
|
urea
|
CO(NH2)2
|
0.1428
|
2
|
|
ammonia
|
NH3
|
0.0714
|
1
|
|
ammonium chloride
|
NH4Cl
|
0.2857
|
4
|
Although Dalton's atomic theory was immediately found to be a useful tool for organizing chemical knowledge, it was some time before it became accepted as a true representation of the world. Thus, as late as 1887, one commentator observed
"Atoms are round bits of wood invented by Mr. Dalton."
These wooden balls have evolved into computer-generated images derived from the atomic force microscope (AFM), an exquisitely sensitive electromechanical device in which the distance between the tip of a submicroscopic wire probe and the surface directly below it is recorded as the probe moves along a surface to which atoms are adsorbed. The general principle of the AFM is quite simple, but its realization in an actual device can appear somewhat intimidating! This highly specialized atomic force microscope is one of several similar devices described at this Argonne National Laboratory.
Relative Masses
Dalton's atomic theory immediately led to the realization that although atoms are far too small to be studied directly, their relative masses can be estimated by observing the weights of elements that combine to form similar compounds. These weights are sometimes referred to as combining weights. There is one difficulty, however: we need to know the formulas of the compounds we are considering in order to make valid comparisons. For example, we can find the relative masses of two atoms X and Y that combine with oxygen only if we assume that the values of n in the two formulas \(XO_n\) and \(YO_n\) are the same. But the very relative masses we are trying to find must be known in order to determine these formulas.
The way to work around this was to focus on binary (two-element) compounds that were assumed to have simple atom ratios such as 1:1, 1:2, etc., and to hope that enough 1:1 compounds would be found to provide a starting point for comparing the various pairs of combining weights. Compounds of oxygen, known as oxides, played an especially important role here, partly because almost all of the chemical elements form compounds with oxygen, and most of them do have very simple formulas.
--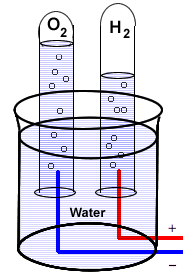
The first proof that water is composed of hydrogen and oxygen was because of the discovery, in 1800, that an electric current could decompose water into these elements. Notice the 2:1 volumes of the two gases displacing the water at the tops of the tubes.
Of these oxygen compounds, the one with hydrogen — ordinary water — had been extensively studied. Earlier experiments had given the composition of water is 87.4 percent oxygen and 12.6 percent hydrogen by weight. This means that if the formula of water is assumed [incorrectly] to be HO, then the mass ratio of the two kinds of atoms must be O:H = 87.4/12.6 = 6.9. Later work corrected this figure to 8, but the wrong assumption about the formula of water would remain to plague chemistry for almost fifty years until studies on gas volumes proved that water is H2O.
Dalton fully acknowledged the tentative nature of weight ratios based on assumed simple formulas such as HO for water, but was nevertheless able to compile in 1810 a list of the relative weights of the atoms of some of the elements he investigated by observing weight changes in chemical reactions.
|
hydrogen
|
nitrogen
|
carbon
|
oxygen
|
phosphorus
|
sulfur
|
iron
|
zinc
|
copper
|
lead
|
|---|---|---|---|---|---|---|---|---|---|
|
1
|
5
|
5.4
|
7
|
9
|
13
|
50
|
56
|
56
|
95
|
Because hydrogen is the lightest element, it was assigned a relative weight of unity. By assigning definite relative masses to atoms of the different elements, Dalton had given reality to the concept of the atom and established the link between atom and element. Once the correct chemical formulas of more compounds became known, more precise combining-weight studies eventually led to the relative weights of the atoms we know today as the atomic weights, which we discuss farther on.
The Nuclear atom
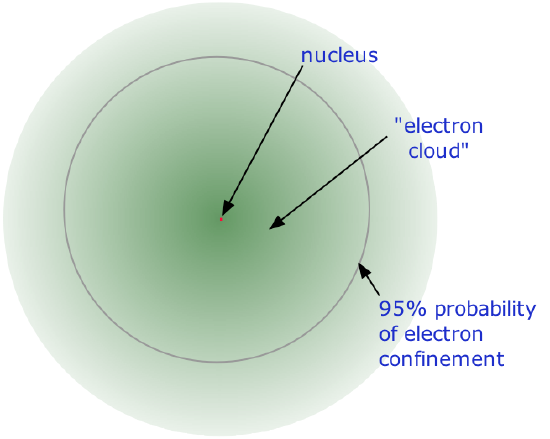
The precise physical nature of atoms finally emerged from a series of elegant experiments carried out between 1895 and 1915. The most notable of these achievements was Ernest Rutherford's famous 1911 alpha-ray scattering experiment, which established that
 •
•
- Almost all of the mass of an atom is contained within a tiny (and therefore extremely dense)nucleus which carries a positive electric charge whose value identifies each element and is known as the atomic number of the element.
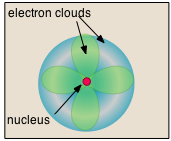
- Almost all of the volume of an atom consists of empty space in which electrons, the fundamental carriers of negative electric charge, reside. The extremely small mass of the electron (1/1840 the mass of the hydrogen nucleus) causes it to behave as a quantum particle, which means that its location at any moment cannot be specified; the best we can do is describe its behavior in terms of the probability of its manifesting itself at any point in space. It is common (but somewhat misleading) to describe the volume of space in which the electrons of an atom have a significant probability of being found as the electron cloud. The latter has no definite outer boundary, so neither does the atom. The radius of an atom must be defined arbitrarily, such as the boundary in which the electron can be found with 95% probability. Atomic radii are typically 30-300 pm.
Protons and Neutrons
The nucleus is itself composed of two kinds of particles. Protons are the carriers of positive electric charge in the nucleus; the proton charge is exactly the same as the electron charge, but of opposite sign. This means that in any [electrically neutral] atom, the number of protons in the nucleus (often referred to as the nuclear charge) is balanced by the same number of electrons outside the nucleus.
Ions
Because the electrons of an atom are in contact with the outside world, it is possible for one or more electrons to be lost, or some new ones to be added. The resulting electrically-charged atom is called an ion.
The other nuclear particle is the neutron. As its name implies, this particle carries no electrical charge. Its mass is almost the same as that of the proton. Most nuclei contain roughly equal numbers of neutrons and protons, so we can say that these two particles together account for almost all the mass of the atom.
Atomic Number (Z)
What single parameter uniquely characterizes the atom of a given element? It is not the atom's relative mass, as we will see in the section on isotopes below. It is, rather, the number of protons in the nucleus, which we call the atomic number and denote by the symbol Z. Each proton carries an electric charge of +1, so the atomic number also specifies the electric charge of the nucleus. In the neutral atom, the Z protons within the nucleus are balanced by Z electrons outside it.

Moseley searched for a measurable property of each element that increases linearly with atomic number. He found this in a class of X-rays emitted by an element when it is bombarded with electrons. The frequencies of these X-rays are unique to each element, and they increase uniformly in successive elements. Moseley found that the square roots of these frequencies give a straight line when plotted against Z; this enabled him to sort the elements in order of increasing atomic number.
You can think of the atomic number as a kind of serial number of an element, commencing at 1 for hydrogen and increasing by one for each successive element. The chemical name of the element and its symbol are uniquely tied to the atomic number; thus the symbol "Sr" stands for strontium, whose atoms all have Z = 38.
Mass number (A)
This is just the sum of the numbers of protons and neutrons in the nucleus. It is sometimes represented by the symbol A, so
\[A = Z + N\]
in which Z is the atomic number and N is the neutron number.
Nuclides and their Symbols
The term nuclide simply refers to any particular kind of nucleus. For example, a nucleus of atomic number 7 is a nuclide of nitrogen. Any nuclide is characterized by the pair of numbers (Z ,A). The element symbol depends on Z alone, so the symbol 26Mg is used to specify the mass-26 nuclide of magnesium, whose name implies Z=12. A more explicit way of denoting a particular kind of nucleus is to add the atomic number as a subscript. Of course, this is somewhat redundant, since the symbol Mg always implies Z=12, but it is sometimes a convenience when discussing several nuclides.
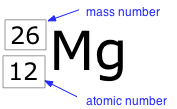
Two nuclides having the same atomic number but different mass numbers are known as isotopes. Most elements occur in nature as mixtures of isotopes, but twenty-three of them (including beryllium and fluorine, shown in the table) are monoisotopic. For example, there are three natural isotopes of magnesium: 24Mg (79% of all Mg atoms), 25Mg (10%), and 26Mg (11%); all three are present in all compounds of magnesium in about these same proportions.
Approximately 290 isotopes occur in nature. The two heavy isotopes of hydrogen are especially important— so much so that they have names and symbols of their own:

Deuterium accounts for only about 15 out of every one million atoms of hydrogen. Tritium, which is radioactive, is even less abundant. All the tritium on the earth is a by-product of the decay of other radioactive elements.
Atomic Weights
Atoms are of course far too small to be weighed directly; weight measurements can only be made on the massive (but unknown) numbers of atoms that are observed in chemical reactions. The early combining-weight experiments of Dalton and others established that hydrogen is the lightest of the atoms, but the crude nature of the measurements and uncertainties about the formulas of many compounds made it difficult to develop a reliable scale of the relative weights of atoms. Even the most exacting weight measurements we can make today are subject to experimental uncertainties that limit the precision to four significant figures at best.
Weighing atoms: Mass Spectrometry
An alternative way of examining the behavior of individual atomic particles became evident in 1912, when J.J. Thomson and F.W. Aston showed that a stream of gaseous neon atoms, broken up by means of an electrical discharge, yielded two kinds of subatomic particles having opposite electrical charges, as revealed by their deflections in externally-applied magnetic and electrostatic fields. (The deflections themselves could be observed by the spots the particles made when they impinged on a photographic plate.) This, combined with the finding made a year earlier by Wilhelm Wien that the degree of deflection of a particle in these fields is proportional to the ratio of its electric charge to its mass, opened the way to characterizing these otherwise invisible particles.
Neutral atoms, having no charge, cannot be accelerated along a path so as to form a beam, nor can they be deflected. They can, however, be made to acquire electric charges by directing an electron beam at them, and this was the basis of the first mass spectrometer developed by Thomson's former student F.W. Aston (1877-1945, 1922 Nobel Prize) in 1919. This enabled him to quickly identify 212 of the 287 naturally occurring isotopes.
The mass spectrometer has become one of the most widely used laboratory instruments. Mass spectrometry is now mostly used to identify molecules. Ionization usually breaks a molecule up into fragments having different charge-to-mass ratios, each molecule resulting in a unique "fingerprint" of particles whose origin can be deduced by a jigsaw puzzle-like reconstruction. For many years, "mass-spec" had been limited to small molecules, but with the development of novel ways of creating ions from molecules, it has now become a major tool for analyzing materials and large biomolecules, including proteins.
The scale of relative weights (the atomic weight scale) we now use is based on \(\ce{^{12}_6C}\), whose relative mass is defined as exactly 12. Atomic weights are the ratios of the weights of an element to the weight of an identical number of \(\ce{^{12}_6C}\) atoms. Being ratios, atomic weights are dimensionless.
From 1850 to 1961, the atomic weight scale was defined relative to oxygen = 16.
A certain number (call it "one zillion") of oxygen atoms weighs 1.200 g. What will be the weight of an equal number of lithium atoms?
Solution
From the atomic weight table, the mass ratio of Li/O = 6.94/16.00, so the weight of one zillion lithium atoms will be
\[ (1.200\; g) \times \dfrac{6.94}{16.00} =0.570\; g \nonumber\]
You can visualize the atomic weight scale as a long line of numbers that runs from 1 to around 280. The beginning of the scale looks like this:

You will notice that the relative masses of the different elements (shown in the upper part) are not all integers. If the nuclei all differ by integral numbers of protons and neutrons that have virtually identical masses, we would expect the atomic weights to be integers. Some are very close to integers (the reason they are not exactly integral will be explained in the next section), but many are nowhere near integral. This puzzling observation eventually led to the concept of isotopes.
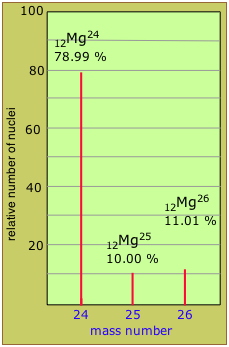
Estimate the average atomic weight of magnesium from the isotopic abundance data shown in the above mass spectrometry plot.
Solution
We just take the weighted average of the mass numbers:
(0.7899 × 24) + (0.1000 × 25) + (0.1101 × 26) = 24.32
Note: The measured atomic weight of Mg (24.305) is slightly smaller than this because atomic masses of nuclear components are not strictly additive, as will be explained further below.
When there are only two significantly abundant isotopes, you can estimate the relative abundances from the mass numbers and the average atomic weight. The following is a favorite exam problem:
The average atomic weight of chlorine is 35.45 and the element has two stable isotopes \(\ce{^{35}_{17}Cl}\) and \(\ce{^{37}_{17}Cl}\). Estimate the relative abundances of these two isotopes.
Solution
Here you finally get to put your high-school algebra to work! If we let x represent the fraction of \(\ce{^{35}Cl}\), then (1-x) gives the fraction of \(\ce{^{37}Cl}\). The weighted average atomic weight is then
35x + 37(1-x) = 35.45
Solving for x gives 2x = 1.55, x = 0.775, so the abundances are 77.5% Cl35 and 22.5% Cl37.
Elemental chlorine, Cl2, is made up of the two isotopes mentioned in the previous example. How many peaks would you expect to observe in the mass spectrum of Cl2?
Solution
The mass spectrometer will detect a peak for each possible combination of the two isotopes in dichlorine: 35Cl-35Cl, 35Cl-37Cl, and 37Cl-37Cl.
Tables of Atomic Weights
are updated every few years as better data becomes available.
One peculiarity you might notice is that the number of significant figures varies from element to element. It tends to be highest for monoisotopic elements, as you can see here for beryllium and fluorine. For some elements, the isotopic abundances vary slightly, depending on the source; this variance reduces the useful precision of a value.
Atomic weights, molecular weights and formula weights
Molecules are composed of atoms, so a molecular weight is just the sum of the atomic weights of the elements it contains.
What is the molecular weight of sulfuric acid, \(H_2SO_4\)?
Solution
The atomic weights of hydrogen and of oxygen are 1.01 and 16.00, respectively (you should have these common values memorized.) From a table, you can find that the atomic weight of sulfur is 32.06. Adding everything up, we have
\[(2 \times 1.01) + 32.06 + (4 \times 16.00) = 98.08\]
Because some solids are not made up of discrete molecules (sodium chloride, NaCl, and silica, SiO2 are common examples), the term formula weight is often used in place of molecular weight. In general, the terms molecular weight and formula weight are interchangeable.
Isotopic Fractionation
The isotopes of a given element are so similar in their chemical behavior that what small differences may exist can be considered negligible for most practical purposes. However, heavier isotopes do tend to react or evaporate slightly more slowly than lighter ones, so that given enough time, various geochemical processes can result in an enrichment of one isotope over the other, an effect known as geochemical isotopic fractionation.
What differences do exist are most evident in the lighter elements, and especially in hydrogen, whose three isotopes differ in mass by relatively large amounts. Thus "heavy water", D2O (2H2O) is not decomposed by electrolysis quite as rapidly as is 1H2O, so it becomes enriched in the the un-decomposed portion of the water in an electrolysis apparatus. Its boiling point is 101.7°C and it freezes at 3.8°. Animals will die if they drink heavy water in place of ordinary water.
The minute differences between the behaviors of most isotopes constitute an invaluable tool for research in geochemistry. For example, the tiny fraction of water molecules containing O18 evaporates more slowly than the lighter (and far more abundant) H2O16. But the ratio of O18 to O16 in the water that evaporates depends on the temperature at which this process occurs. By observing this ratio in glacial ice cores and in marine carbonate deposits, it is possible to determine the average temperature of the earth at various times in the past.
Atomic masses
Here again is the beginning of the atomic weight scale that you saw above:

You understand by now that atomic weights are relative weights, based on a scale defined by 6C12 = 12. But what is the absolute weight of an atom, expressed in grams or kilograms? In other words, what actual mass does each unit on the atomic weight scale represent?
The answer is 1.66053886 × 10–27 kg. This quantity (whose value you do not need to memorize) is known as the unified atomic mass unit, denoted by the abbreviation u or amu. The unified atomic mass unit is defined as 1/12 of the mass of one atom of carbon-12. Fortunately, you do not need to memorize this value, because you can easily calculate its value from Avogadro's number,NA, which you are expected to know:
\[1\, u = \dfrac{1}{N_A} \;g = \dfrac{1}{1000\; N_A} \;Kg\]
Note: Definition of Atomic Mass Unit
The unified atomic mass unit is defined as 1/12 of the mass of one atom of carbon-12.
Masses of the Subatomic Particles
Atoms are composed of protons, neutrons, and electrons, whose properties are shown below:
|
particle
|
mass, g
|
mass, u
|
charge
|
symbol
|
|---|---|---|---|---|
| electron | 9.1093897 × 10–28 | 5.48579903 × 10–4 | 1– | \(\ce{_{–1}^{0}e}\) |
| proton | 1.6726231 × 10–24 | 1.007276470 | 1+ | \(\ce{_1^0H^{+}}\) or \(\ce{_1^0p}\) |
| neutron | 1.6749286 × 10–24 | 1.008664904 | 0 | \(\ce{_1^0n}\) |
Two important points should be noted from Table \(\PageIndex{1}\):
- The mass of the electron is negligible compared to that of the two nuclear particles;
- The proton and neutron have masses that are almost, but not exactly, identical.
Nuclear Masses
As we mentioned in one of the problem examples above, the mass of a nucleus is always slightly different from the masses of the nucleons (protons and neutrons) of which it is composed. The difference, known as the mass defect, is related to the energy associated with the formation of the nucleus through Einstein's famous formula e = mc2. This is the one instance in chemistry in which conservation of mass-energy, rather than of mass alone, must be taken into account. But there is no need for you to be concerned with this in this part of the course.
For all practical purposes, until you come to the section of the course on nuclear chemistry, you can consider that the proton and neutron have masses of about 1 u, and that the mass of an atom (in u) is just the sum of the neutron and proton numbers.


