2.2: A Layer of Metal Atoms
- Page ID
- 189613
Metals are composed of atoms in ordered layers. These atoms form a three-dimensional, crystalline structure. That means that the individual units within the solid -- the atoms, in this case -- are organized in a regularly repeating pattern, like the stars on the American flag.
Three-dimensional things can be difficult to think about. It's much easier to start in two dimensions. On this page, we're going to look at a couple of ways that metal atoms could arrange themselves in a single layer. We'll build up from there later on. In the meantime, we'll try to develop familiarity with a number of terms that are used to describe crystalline structures.
Simple Squares
We live in a Cartesian society. Our houses and buildings are mostly square, our rooms are square, our streets are straight and meet at right angles, unless we live in a meandering place on the water, like Boston or Venice. It's probably easiest to imagine layers of atoms that form nice squares.
Suppose a group of atoms forms a nice, straight line. Another group forms a second line, and each atom in the second line sits directly behind an atom in the first line. A third row forms in the same way. The resulting layer has neat rows and columns of atoms. The pattern of atoms regularly repeats as you look from right to left, and as you look from front to back.
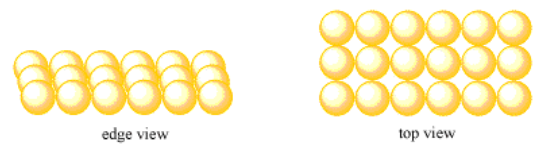
We will call this type of layer a simple square layer.
- In a square layer, atoms are arranged in rows and columns.
Hexagonal Layers
Some metals atoms may be arranged in simple square layers. Others adopt a slightly different arrangement.
Start with the same, neat line of atoms in the first row. This time, when the second row of atoms forms, we won't put them directly behind the atoms in the first row. We'll put them just in between the atoms in front. Each atom in the second row sits behind two atoms in the first row, as if it were peeking between them, like kids in a kindergarten class photo (before they all squirm around).
The third row will also be slightly offset from the row in front of it. If you look carefully, you can see that puts each of the third row atoms directly behind an atom in the first row, but an extra row farther away. The fourth row will be slightly offset from the third, and so on.
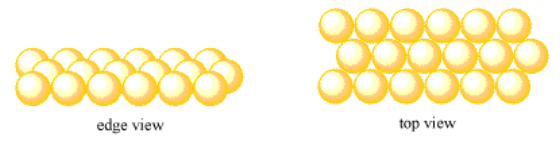
We still have a crystalline structure. There is a regularly repeating pattern as we look from left to right. There is also a repeating pattern as we move from front to back, but now that pattern repeats every other row, instead of every row.
This type of layer is called a hexagonal layer. Sometimes, it is called a close-packed layer.
- In a hexagonal layer, the rows are offset from each other by half an atom.
- Each atom in a hexagonal layer is surrounded by six other atoms.
- Look at the simple square layer. Can you find repeating patterns in other directions (rather than left-right or front-back)? If so, in what direction?
- Look at the hexagonal layer. Can you find repeating patterns in other directions (rather than left-right or front-back)? If so, in what direction?
- Answer a:
-
The pattern also repeats diagonally.
- Answer b:
-
The pattern also repeats diagonally.
We usually think of atoms as little spheres, or circles if we are working in just two dimensions. How might other shapes form an organized layer? Draw an organized layer for each of the following shapes, using about a dozen units in each case.
- squares.
- triangles (equilateral: all sides the same length).
- hexagons.
- pentagons.
In each case, is there only one way to pack the shapes in a regular way? Can you find repeating patterns in the layer? If so, in what direction?
Are there any shapes that seemed more difficult to arrange in a repeating layer?
- Answer
-
The squares can form a number of regularly repeating patterns. The rows can exactly repeat (an aaa pattern), or they can be shifted slightly, so that every other row exactly repeats the first row (an ababab pattern). They could even be shifted so that every third row is an exact repeat of the first (abcabcabc).
The pentagons do not form a repeating layer in two dimensions.
Holes
Unlike some other geometric shapes, circles do not pack together with no space in between them. The spaces in between atoms within a layer are called holes. Note that the use of the word "holes" here has nothing to do with holes in conductivity-speak. On this page, holes are just spaces between atoms. In conductivity, holes are places where there is positive charge that could capture an electron.
Sometimes, the spaces between the atoms are described in other ways, such as "interstitial sites".
Later on, these interstitial sites or holes will be important in building compounds from mixtures of elements. You will see that the empty spaces in an array of atoms leave room for a second kind of atom to pack into the same structure.
Holes generally have particular shapes. The shapes vary, depending on how the atoms are arranged. For example, how would you describe the shape of the holes in the following layers:
- simple square packing.
- hexagonal or close packing.
- Answer a:
-
In the simple square packing, the holes are roughly diamond shaped.
- Answer b:
-
In the hexagonal pattern, the holes are roughly triangular.
You can come up with an answer by looking at a drawing, or you can try packing a layer of dimes or pennies or quarters (as long as they are all the same) and look at the spaces between them
Unit Cells
The simplest repeating unit in a pattern is sometimes called the unit cell. In a layer, the unit cell can be traced again and again over the layer, so that every part of the layer is accounted for (but depending where you start tracing, you might run out of room at the edges).
Because each layer is composed of individual atoms, we might call a single atom the unit cell. However, we also use the unit cell to illustrate the spatial relationship between the atoms in the layer. For that reason, we often shift the unit cell to show multiple atoms.
For example, in a row of atoms, a unit cell might be a square. The ends of the square would cut through two neighbouring atoms. The unit cell contains two half-atoms, for a total of one atom. The square could be repeated in a straight line to reproduce the row of atoms.
- The unit cell is the smallest repeating unit in the structure.
- The unit cell shows the pattern that is found in the structure.
In a layer of atoms, the unit cell might once again be thought of as a single atom. However, we can more clearly show the relationships between these atoms by choosing a slightly different cell. The unit cell in a simple square layer is just a square that contains the corners of four neighbouring atoms. The unit cell in a hexagonal layer is a rhombus that contains the corners of four neighbouring atoms.
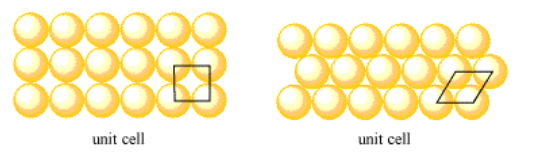
In the following cases, show that the given unit cells repeat throughout the structure.
- simple square layer: a square unit cell
- hexagonal layer: a rhombic unit cell
Note: in the hexagonal layer, you can find an additional way to do this if you rotate copies of the unit cell to get unit cells facing in three different directions.
In the following cases, show what fractions of atoms are found in the unit cell. Add the fractions to find the combined total of atoms in the unit cell.
- simple square layer: a square unit cell
- hexagonal layer: a rhombic unit cell
Packing Efficiency
Packing efficiency is one of the questions people wonder about in crystal structures. It deals with how tightly the atoms are packed together in a structure. Often, the more tightly packed the structure, the better (but it does not always happen that way).
Why might tighter packing of metal atoms be favored? It has to do with the fact that the metal atoms are interacting with each other. The closer they are together, the more strongly they can interact.
There are a couple of ways we can think about that interaction. In the simplest idea of the electron-sea model, metal atoms have become metal cations, and are surrounded by electrons. The closer the metal atoms can get to the electrons, the more strongly they will interact. In general, we think of the metal atoms as sharing their electrons; the closer the metal atoms are to each other, the more efficiently the electrons can be shared.
Let's just work with that idea of electrostatic attraction. Imagine a group of atoms in a simple square layer. All of the atoms are touching their neighbors on either side. Let's think about the distance between a nucleus and an individual electron in the electron sea. We know that the nucleus is in the center of the atom. We don't know exactly where a free electron is, but let's assume it is in the center of the nearest hole. Remember, the closer the electron is to the nucleus, the lower the energy.
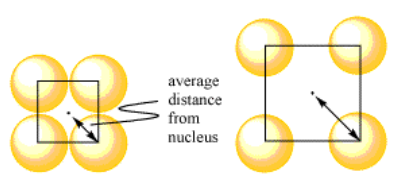
For comparison, maybe there is another set of atoms, also in a simple square layer. Suppose they are well-separated from each other; maybe they are far enough apart that you could fit an extra atom between each pair if you wanted to. If the free electron is in the same place -- the middle of the nearest hole -- you can see that it is much farther from the nucleus in this case. The force of attraction is much lower in this case, and the overall energy is not as low.
- Most metals pack very efficiently together to form a solid.
- Efficient packing leads to stronger bonding interactions.
That first case, with atoms packed more tightly together, may be preferable, because of the stronger interaction between the metal nucleus and the free electron. For reasons like this, understanding the packing efficiency in a crystal can be very important.
Go to your piggy bank and break out a bunch of pennies, nickels, quarters or dimes. You will need at least four of each, but nine of them is a good number. Pack one type of coin into the following layers:
- simple square
- hexagonal or close packed
- Answer a:
-
Using quarters, the distance is about 5 mm.
- Answer b:
-
Using quarters, the distance is about 2.5 mm.
A free electron would be closer to the atoms in a hexagonal close packed layer. There would be stronger electron-ion attraction in that case.
In each case, measure the distance from the edge of one coin to the center of the hole.
In which case is the free electron closer to the atom? Does the packing system (the type of layer) have an effect on how tightly bonded that atoms are?
Go to your piggy bank and break out a bunch of quarters AND a bunch of dimes. You will need at least four of each, but nine of them is a good number. Pack each type of coin into the following layers:
- simple square
- hexagonal or close packed
- Answer a:
-
Using dimes, the distance is about 3.5 mm.
- Answer b:
-
Using dimes, the distance is about 1.5 mm.
A free electron would be closer to the atoms if the atoms were smaller. There would be stronger electron-ion attraction in that case.
In each case, measure the distance from the edge of one coin to the center of the hole.
In which case is the free electron closer to the atom? Does the size of the atom have an effect on how tightly bonded that atoms are?
When a metal melts, the atoms go from a tightly-bound, regular array of atoms to a loosely-bound set of mobile atoms.
Compare the melting points of the following metals, given in degrees Celsius.
potassium: 64 cesium: 29 lithium 181 sodium: 98 francium: 27
- Can you determine any trends among these values?
- Can you provide a physical explanation for your observation? (You may have found a trend, but can you explain it?)
- Answer a:
-
melting points (and force of attraction between atoms): Fr < Cs < K < Na < Li
- Answer b:
-
This trend mirrors the sizes of the atoms. Lithium is the smallest and francium the largest. The electron / ion attraction is greatest in Li and weakest in Fr.
Packing efficiency is often determined more rigorously in terms of the percentage of a unit cell that is actually occupied by atoms. What is the total area of a unit cell in the following layers?
- simple square layer.
- hexagonal layer.
- Answer a:
-
The total area of this square is
\[Area = w^{2} \nonumber\]
in which w = width of the unit cell. The width of the unit cell is
\[w = 2r \nonumber\]
in which r = radius of titanium atom.
\[Area = 4r^{2} = 4 (2.00 \times 10^{-10} m)^{2} = 4(4.00 \times 10^{-20} m^{2}) = 1.60 \times 10^{-19} m^{2} \nonumber\]
- Answer b:
-
The total area of this rhombus is
\[Area = s^{2} sin \theta \nonumber\]
in which s = one side of unit cell and θ = an angle of the unit cell (either 60° or 120°). But
\[s = 2r \nonumber\]
in which r = radius of titanium atom.
\[Area = (2 \times 2.00 \times 10^{-10} m)^{2} sin (60) = 1.60 \times 10^{-19} (0.87) m^{2} = 1.39 \times 10^{-19} m^{2} \nonumber\]
You can assume the atoms are titanium. Titanium has an atomic radius of 2.00 Angstroms (or 2.00 x 10-10 m).
How many titanium atoms are there in a unit cell in the following layers?
- simple square layer.
- hexagonal layer.
- Answer a:
-
\[4 \times \frac{1}{4} = 1 \: atom \nonumber\]
- Answer b:
-
\[2 \times \frac{1}{6} + 2 \times \frac{1}{3} = \frac{2}{6} + \frac{4}{6} = 1 \: atom \nonumber\]
You may need to add up fractions of titanium atoms to arrive at the answer. The answer may or may not be a whole number.
What is the area occupied by a titanium atom?
(If you think the question is ambiguous, assume we're concerned about the area of a cross-section of the atom at its widest part. It is a spherical atom, but we are dealing with its projection in two dimensions, i.e. its shadow when the sun is directly overhead.)
- Answer
-
The cross-sectional (two dimensional) area of a titanium atom is the area of a circle
\[Area = \pi r^{2} \nonumber\]
\[Area = 3.1415 \times (2.00 \times 10^{-10} m)^{2} = 3.1415 \times 4.00 \times 10^{-20} m^{2} = 1.257 \times 10^{-19} m^{2} = 1.26 \times 10^{-19} m^{2} \nonumber\]
In the following cases, what percentage of the unit cell is filled with titanium atoms?
- simple square layer.
- hexagonal layer.
- Answer a:
-
\[Efficiency = \frac{occupied}{total} \times 100 \% = \frac{1.26 \times 10^{-19} m^{2}}{1.39 \times 10^{-19} m^{2}} \times 100 \% = 91 \% \nonumber\]
- Answer b:
-
\[Efficiency = \frac{occupied}{total} \times 100 \% = \frac{1.26 \times 10^{-19} m^{2}}{1.39 \times 10^{-19} m^{2}} \times 100 \% = 91 \% \nonumber\]
A greater percentage of space is occupied in hexagonal close packing.
The percentage of unit cell that is occupied by atoms is called "the packing efficiency".
Coordination Number
There are a number of terms used in describing the relationships between atoms and the atoms to which they are directly bonded. For example, we use the term "coordination number" to describe the number of other atoms that a specific atom is touching in a regular layer.
What is the coordination number of an atom in
- simple square layer
- hexagonal layer
- Answer a:
-
coordination number = 4
- Answer b:
-
coordination number = 6
What is the coordination number of an atom in the following layers:
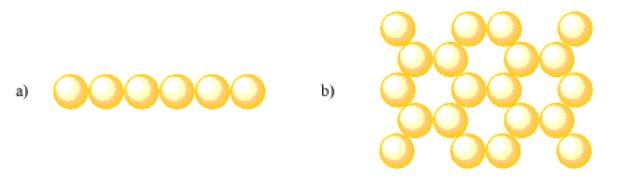
- Answer a:
- Answer b:
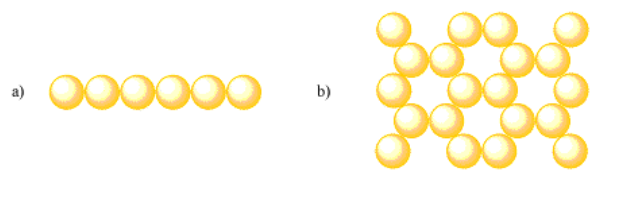
Answer a:Assuming the pattern extends linearly, coordination number = 2. Otherwise, coordination number = 2 for interior atoms and coordination number = 1 for terminal atoms.Answer b:Assuming the pattern extends in two dimensions, coordination number = 3. Otherwise, coordination number = 3 for interior atoms, coordination number = 2 for side edge atoms and coordination number = 1 for corner atoms.Images for Exercise 2.2.14 a and b. a is a single row of six atoms. b is a hexagonal arrangement of atoms; each hexagon has an empty center and is composed of six atoms.
Coordination Geometry
Take a look at all of the atoms surrounding one specific atom in a layer. If you were to draw a line from the center of one of these atoms to the next, and go all the way around until you got back to the beginning, you would get a specific shape. That shape is described as the coordination geometry of the central atom. It's closely related to the coordination number. In two dimensions, two atoms with the same coordination number always have the same coordination geometry. Occasionally in three dimensions, two atoms with the same coordination number can have different coordination geometries; the atoms that they are touching may be arranged in slightly different ways.
What is the coordination geometry of an atom in
- simple square layer
- hexagonal layer
What is the coordination geometry of an atom in the following layers:
Lattice
Sometimes, the arrangement of atoms in a crystal is referred to as "an array" or "a lattice". At this point, an array or lattice is just the two-dimensional network of atoms in a layer. Later, we will see three-dimensional arrays of atoms. Metallic solids are usually three-dimensional, not two-dimensional. However, as we start to build up to a third dimension, you will see that most of the ideas on this page have analogies in 3D.