2.3: Building Metal Atoms in Three Dimensions
- Page ID
- 189614
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)What sort of structures compose the world around us? What sort of shapes do we see in the building blocks of the material world? The ancient Greeks placed special significance on certain perfect shapes, or Platonic solids. These shapes were considered to be perfect because they were so regular, with equally sized sides arranged at identical angles to each other, so that the solid would look the same when viewed from different angles. For example, a cube has four square sides, all connected at right angles to each other. These Platonic solids were sometimes associated with the classic elements as perceived at the time: earth, air, fire and water.
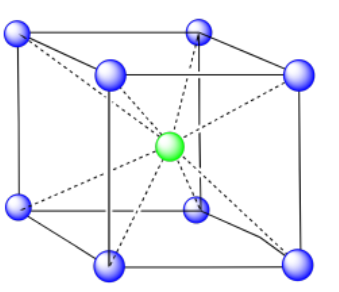
As it happens, the Greeks were not that far from the truth. Certain solids do appear frequently in the structures of nature, including the classic Platonic solids. These shapes just happen to describe the natural way that a group of atoms might arrange themselves when they come together to build a larger structure. Very often, we find an atom at the center of a Platonic solid, with other atoms arranged around it to form the corners of the solid.
In addition to the cube shown above, the tetrahedron and octahedron are extremely common Platonic solids found in natural structures. A couple of non-Platonic solids that we sometimes see are the square pyramid (think of the ones in Egypt) and the trigonal bipyramid; however, we won't encounter those in nature for a few more chapters.
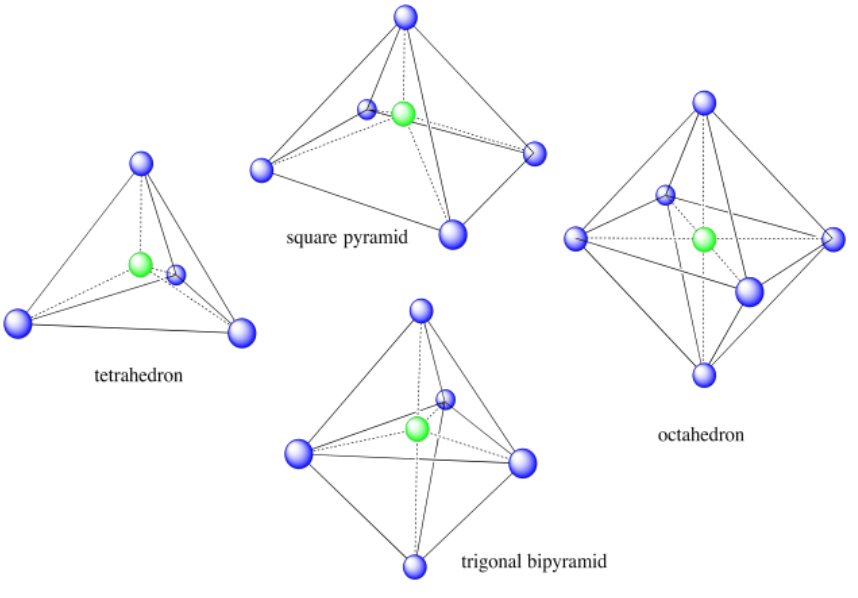
For each of the following solids, identify the number of (i) corners and (ii) faces.
a) cube b) tetrahedron c) square pyramid d) trigonal bipyramid e) octahedron
- Answer a:
-
(i) 8
(ii) 6
- Answer b:
-
(i) 4
(ii) 4
- Answer c:
-
(i) 5
(ii) 5
- Answer d:
-
(i) 5
(ii) 6
- Answer e:
-
(i) 6
(ii) 8
We will see cubic, octahedral and tetrahedral shapes cropping up as we look at the structures of extended solids such as metals and salts. In the solid state, metals are very neat, orderly structures. Metal atoms form a three-dimensional, crystalline structure. We will start thinking about those structures by seeing how they can be built up from simpler, two-dimensional layers.
Building up from Squares: Simple Cubic Packing
Take a simple square layer of atoms. Suppose another layer forms on top of that one, with atoms arranged in the same way as the first layer. Each atom in the second layer sits directly on top of an atom in the first layer.
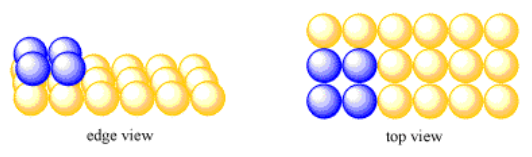
This is a very neat, ordered, simple structure. All of the atoms are lined up in straight rows, aisles and columns. The structure looks exactly the same if viewed along the x-axis, along the y-axis, or along the z-axis.
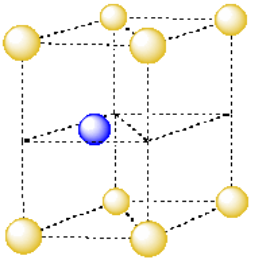
The simplest repeating unit in three dimensions is usually thought of as a box or cube with atoms at each of its eight corners. Alternatively, we might think of the repeating unit as a cube with one atom in its center. However, it's useful to see the relationships between multiple atoms in the unit cell. For that reason, we usually picture the unit cell as the cube with an atom at each corner. Because each of those corners is shared between several unit cells, it is better to think of each unit cell as only owning a fraction of each corner atom.
- A simple cubic unit cell is based on a square layer.
- Squares of atoms are repeated in the x, y and z directions.
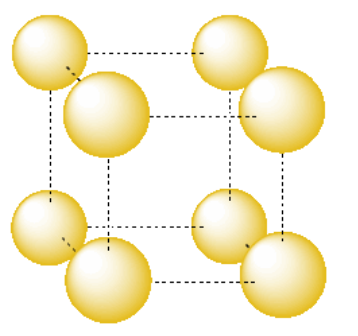
In the following sections, unit cells will be shown with atoms separated even further from each other because the relationships between the atoms are even more complex. In the case of a simple cubic packing system, the unit cell would be shown as follows:
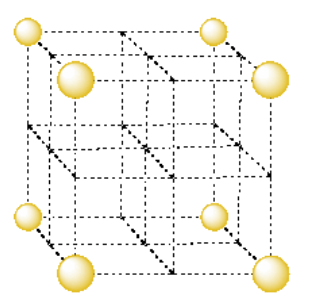
Take a look at the simple cubic unit cell.
- What fraction of an atom is found in each corner of the simple cubic unit cell?
- How many corners are there in the cube?
- What is the total number of atoms in the simple cubic unit cell?
- Answer a:
-
1/8 atom at each corner
- Answer b:
-
8 corners in a cube
- Answer c:
-
\(8 \times \frac{1}{8} = 1\) atom per simple cube
Building up from Squares: Body-Centered Cubic Packing
That isn't the only way a three-dimensional solid could be built up from a simple square layer. Remember from the discussion of layers that atoms can sit a little more tightly together by staggering, so that one atom does not sit directly behind another. Instead, an atom in the second row sits behind a pair of atoms in the first row, and right in between them as viewed from the front. This sort of staggering happens easily in three dimensions, too.
In fact, if you take four oranges and make a square with them, and then decide to place a fifth orange on top of that layer, where is the obvious place to put this last orange? You would put it right in the middle of the first four, perched in the little valley on top of them.
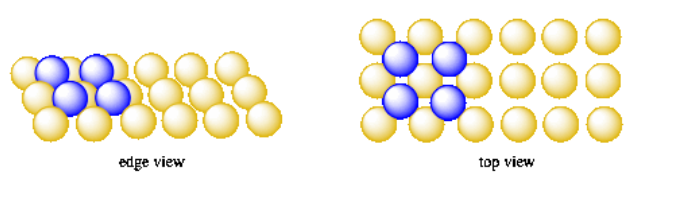
If you have a whole produce box full of oranges, you can make a bigger first layer of oranges, and start placing additional oranges in all of the little square valleys between the oranges of the first layer. Soon you will find that you have built a second, simple square layer. It is just like the first layer, but offset by half a unit cell to the side and half a unit cell to the back.
You can keep adding more layers until you run out of oranges or the whole thing falls down and rolls away. If you do so, you might notice that all the oranges in the third layer sit directly above the oranges in the first layer, and all the oranges in the fourth layer sit directly above the ones in the second layer. That's because each new layer is offset by half a unit cell, so every two layers, that shift adds up to one unit cell, and the oranges line up again. This pattern is sometimes described as an ABABAB pattern; that means the odd layers line up exactly with each other, and the even layers line up exactly with each other.
- Body-centered cubic packing allows the second layer of atoms to get a little closer to the atoms in the first layer.
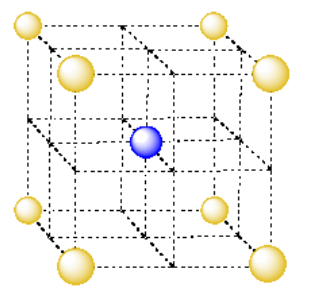
The unit cell in this system, like the simple cubic system, is a cube with an eighth of an atom (or orange) at each corner. However, the corner atoms are not found in adjacent layers, but in alternating layers (such as the first and the third). An atom from the middle layer is also included in the cell; the entire atom is right in the center of the unit cell. This packing system is called body-centered cubic.
- The unit cell of a body-centered cubic system is a lot like the simple cubic unit cell.
- The body-centered cubic unit cell has an extra atom in its center.
One important note: in a body-centered cubic system (and the other systems to follow), the atoms in the first layer are not quite touching each other. By backing off slightly from each other within a layer, there are closer interactions from one layer to another. The extra room allowed by spreading an individual layer out a little bit allows subsequent layers of atoms to nestle more deeply in those valleys. Stronger bonding interactions result from those close connections between layers.
By the way, you would have a hard time building up a simple cubic structure with oranges, unless you glued them together or used slightly flattened oranges, like clementines. There is more structural support in the body-centered cubic structure, because the oranges resting in valleys are distributing their weight to and getting support from four oranges beneath them, not just one.
Take a look at the body-centered cubic unit cell.
- What fraction of an atom is found in each corner of the body-centered cubic unit cell?
- How many corners are there in the cube?
- Are there atoms anywhere else in the cube?
- What is the total number of atoms in the body-centered cubic unit cell?
- Answer a:
-
1/8 atom at each corner
- Answer b:
-
8 corners in a cube
- Answer c:
-
1 atom in middle of cube
- Answer d:
-
\(1 + 8 \times \frac{1}{8} = 2\) atoms per body-centered cube
Building up from Hexagonal Layers: Hexagonal Close Packing
Some metal atoms form hexagonal layers. Instead of being in close contact with four neighbouring atoms in a layer, an atom in a hexagonal layer is in close contact with six neighbouring atoms.
Do you still have your oranges? Suppose you start with a hexagonal layer of them. When another layer of oranges is added on top of a hexagonal layer, the new oranges don't sit right on top of the ones in the first layer. Instead, they sit in the little valleys between the oranges of the first layer. This is a little like the second layer of body-centered cubic packing. The difference is, in body centered cubic packing, all of the valleys between the oranges of the first layer are occupied by oranges from the second layer. In hexagonal packing, each orange in the first layer has six small valleys around it. You can't easily fit six oranges into all of those valleys at the same time; there isn't enough room. Instead, only every other valley is occupied by an orange, forming the second layer.
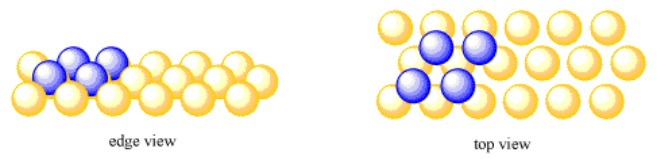
In the drawing, you might notice that the atoms in one layer are separated slightly from each other. That's also to the second layer of atoms to fit more deeply into the valleys between the atoms in the first layer. Some close interaction between the atoms within a layer is given up in order to get better interactions between the atoms in different layers. It's a trade-off that leads to slightly stronger interactions overall.
Again, just like the systems based on simple squares, the second layer that forms looks a lot like the first. It is another hexagonal layer. It is shifted away from the first layer by half an atom to the side, and half an atom to the front or back.
- Hexagonal layers are not usually stacked with atoms directly on top of each other.
- Hexagonal layers get a little closer to each other by shifting so that atoms above can sit in valleys below.
- There isn't room for every valley to be occupied by an atom. Every other valley is left open.
Once we begin to add a third layer, we have a choice. Just like with the second layer, we can't add a new orange into every valley. We will have to add them into every other valley. We can either add them directly over the oranges in the first layer, or directly over the valleys that were left empty when we filled in the second layer.
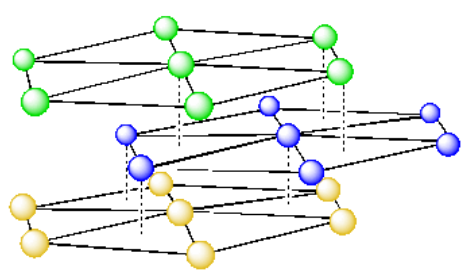
Let's put them directly over the oranges in the first layer. When we add the oranges for the fourth layer, we'll put them directly over the ones in the second layer. This system of packing is called hexagonal close-packing.
- In hexagonal close packing, the third layer of atoms is directly above the first layer.
- This system is a little like body-cenetered cubic, but with a hexagonal base instead of a square one.
Before we consider the unit cell in this system (which is a little more complicated than in the cubic packing systems), let's take a look at these layers of atoms, with a little bit greater separation.
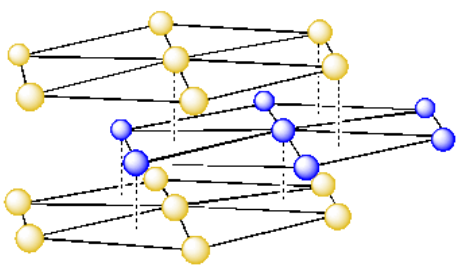
Because the atoms in the top layer are directly over the atoms in the bottoms layer, we can think of these two layers as being identical. We can show that by drawing them in the same color.
In a hexagonal single layer, the unit cell was a rhombus. We could use that to build the unit cell for a hexagonal close packed system. We would just add walls into the cell to build the simplest repeating unit.
The pattern of layers in the simple cubic packing system was AAAAAA; each layer was placed so that each atom was directly above an atom in the layer below it. The pattern of layers in the body centered cubic arrangement was ABABAB; each atom in a layer was directly above one that was two layers down. Which pattern fits hexagonal close packing?
- Answer
-
Hexagonal close packed pattern is ABAB.
Take a look at the hexagonal close-packed unit cell.
- What fraction of an atom is found in each corner of the hexagonal close-packed cubic unit cell?
- Adding up all those fractions, how many corner atoms are within the cell?
- Are there atoms anywhere else in the cell?
- What is the total number of atoms in the hexagonal close-packed unit cell?
- Answer a:
-
At both the top and bottom layer, two atoms are 1/3 within the cell and two atoms are 1/6 within the cell.
- Answer b:
-
That makes \(2 \times (2 \times \frac{1}{3} + 2 \times \frac{1}{6}) = \frac{4}{3} + \frac{4}{6} = \frac{4}{3} + \frac{2}{3} = 1\) atom total in corners
- Answer c:
-
1 atom inside the cell.
- Answer d:
-
2 atoms total.
In the following variation on hexagonal close packing, the two unit cells appear to be slightly different.
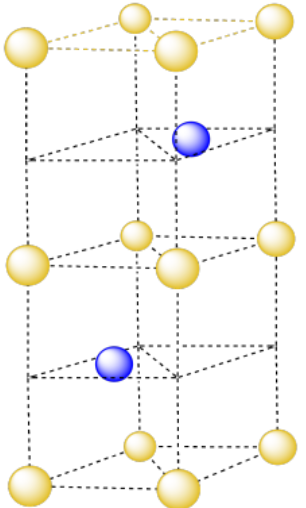
- What is the relationship between the two unit cells in the above structure?
- How would you describe the relationships between the layers in the above structure (i.e. ABCABC etc)?
- Answer
-
The pattern in this variation is ABACA.
Building up from Hexagonal Layers: Cubic Close Packing (or Face-Centered Cubic Packing)
Start with the same hexagonal layer of oranges. Once again, when another layer is added on top of that hexagonal layer, the new oranges don't sit right on top of the ones in the first layer. Instead, they sit in the little valleys between the oranges of the first layer. Remember, in hexagonal packing, each orange in the first layer has six small valleys around it. You can't easily fit six oranges into all of those valleys at the same time; there isn't enough room. Instead, only every other valley is occupied by an orange, forming the second layer.
Again, just like in the other systems, the second layer looks a lot like the first. It is another hexagonal layer. It is shifted away from the first layer.
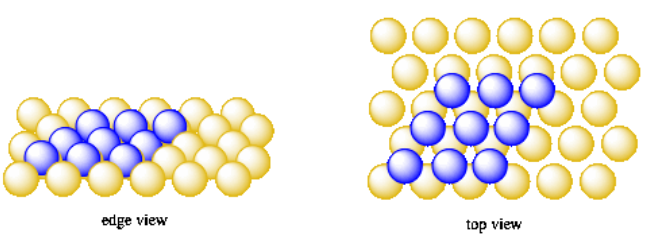
Once we begin to add a third layer, we have a choice. Just like with the second layer, we can't add a new orange into every valley. We will have to add them into every other valley. We can either add them directly over the oranges in the first layer, or directly over the valleys that were left empty when we filled in the second layer.

This time, let's put them directly over the holes in the first layer that were not filled before. When we add the oranges for the fourth layer, we'll put them directly over the oranges in the first layer. The oranges in the fifth layer will sit above the ones in the second layer, and the ones in the sixth layer will sit over those in the third layer.
- In cubic close-packing, the layers are actually hexagonal (also called "close-packed").
- In the third layer, the atoms do not lie directly above atoms in the first layer.
- Instead, the atoms in the third layer sit above the empty valleys from the first layer.
This system of packing is called cubic close-packing or face centered cubic packing.
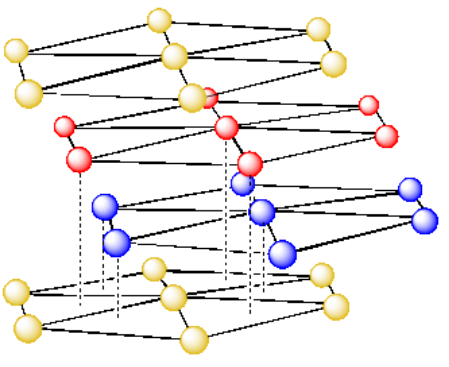
The pattern of layers in the simple cubic packing system was AAAAAA. The pattern of layers in the body centered cubic arrangement was ABABAB. How would you describe the pattern in cubic close-packing?
- Answer
-
ABCABC.
The unit cell in the hexagonal close-packed system was based on a unit cell from a single layer. Propose a similar unit cell for a cubic close-packed system.
- What two-dimensional unit cell forms the base of this three-dimensional unit cell?
- How many layers does the cubic close-packed unit cell cut through?
- Draw the cubic close-packed unit cell.
- Answer a:
-
The rhombus-shaped hexagonal unit cell.
- Answer b:
-
4 layers.
Hey, wait a minute. Why do they call it cubic packing if the unit cell is based on a rhombus instead of a square? Maybe there is another way of looking at this structure. Maybe there is an alternative unit cell.
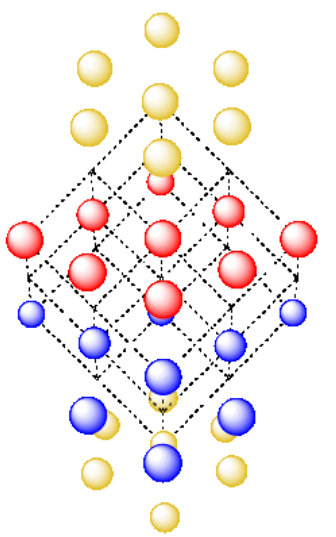
There is a cubic unit cell, but it is harder to see. The cube is tipped on one of its corners. We will strip away some of the extra atoms in the hexagonal layers so we can get a better look.
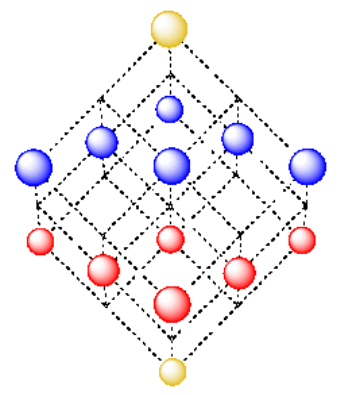
There is an atom in the lowest layer that forms one corner of the cube. The opposite corner of the cube is an atom in the fourth layer. That atoms sits directly above the one in the first layer, the bottom corner of the cube. In between, three faces of the cube are tilted downwards. There is an atom in the middle of each of these faces; together with atoms at the three corners in between them, these form a second layer in the structure. There are also three faces tilted upwards. There is an atom in the center of each of these faces; together with atoms at the three corners in between them, these form a third layer in the structure.
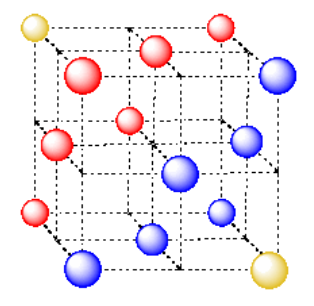
Note that this cube has an atom in the center of each face; hence the name, face-centered cubic.
- A cubic close-packed takes the name "cubic" from the presence of a cubic unit cell.
- This cubic unit cell is oriented diagonally to the close-packed layers.
- This cubic unit cell has an atom in the ceneter of each face; it is also called "face-centered cubic".
Take a look at your new cubic close-packed unit cell.
- What fraction of an atom is found in each corner of the cubic close-packed cubic unit cell?
- How many corners are there in the cell?
- Are there atoms anywhere else in the cell?
- What is the total number of atoms in the cubic close-packed unit cell?
- Answer a:
-
1/8 atom at each corner
- Answer b:
-
8 corners in a cube
- Answer c:
-
1/2 atom on each face of cube
- Answer d:
-
\(6 \times \frac{1}{2} + 8 \times {1}{8} = 4\) atoms per face-centered cube
The type of packing adopted by a metal actually has some influence on the physical properties of the metal. For example, the metals that are closely associated with metal-working during antiquity, such as lead, gold, silver, and copper, generally adopt cubic close-packed structures. These metals have high values of "physical ductility" -- an index of how easily they can be stretched into wire. Titanium, cobalt, and zinc are hexagonal close-packed and have moderate values of physical ductility. Metals that adopt body-centered cubic packing, such as iron, tungsten, and chromium, usually have lower physical ductility.
This trend isn't a strict rule; some body-centered metals are more ductile than some cubic close-packed metals. Nevertheless, metal packing seems to be one factor in how easily metals can be stretched, bent, and worked. The reason it plays a role is because of the presence of "slip planes" in metal structure. Remember the idea that rows of metal atoms can slide across each other? It turns out that cubic close-packed metals form rows in lots of different directions, so their atoms can slip past each other pretty easily. In contrast, that central atom in a body-centered cubic cell acts like a speed bump for the layer of atoms above and below it, slowing down their movement.
We saw previously that the number of near neighbors of a metal atom is called the coordination number. What is the coordination number in each of the following cases?
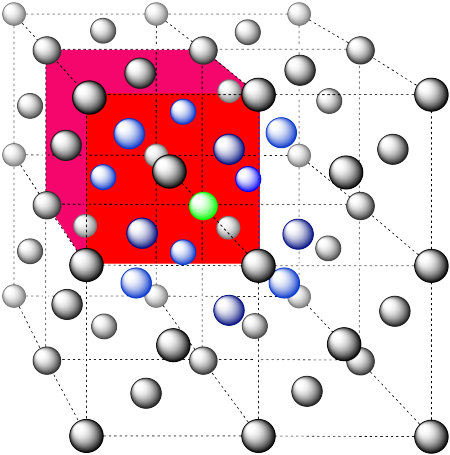
- an atom at the corner of a simple cubic cell. Remember, it is surrounded by other unit cells, too.
- an atom in the center of a body-centered cubic cell.
- an atom in the corner of a body-centered cubic cell.
- an atom in the corner of a face-centered cubic cell.
- an atom on the face of a face-centered cubic cell.
- Answer a:
-
coordination number = 6 (3 within the cube, along the three adjacent edges, plus three on adjacent cubes).
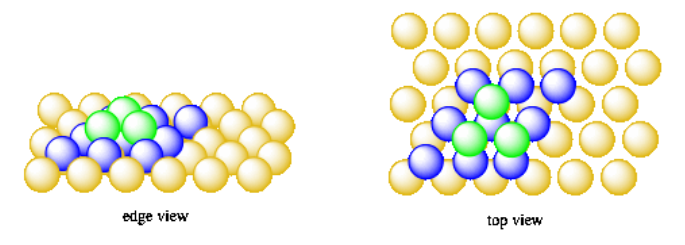
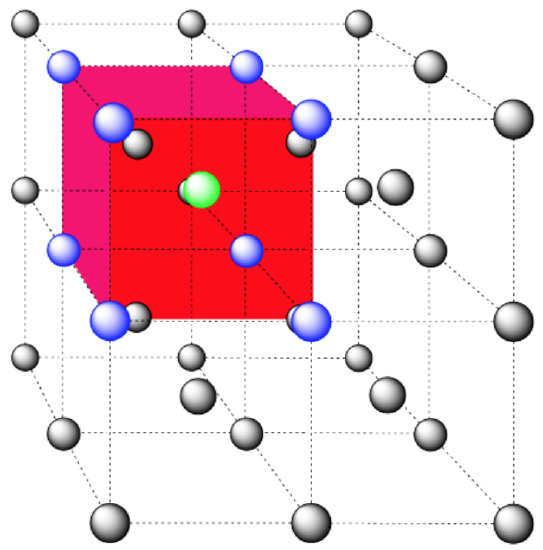
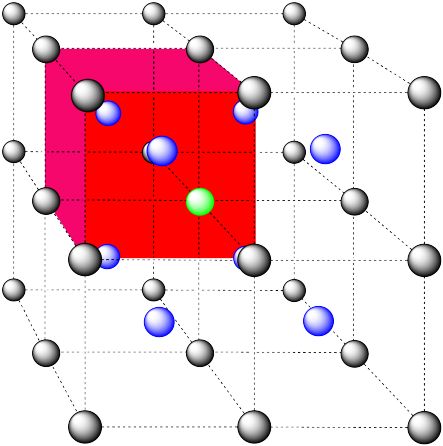
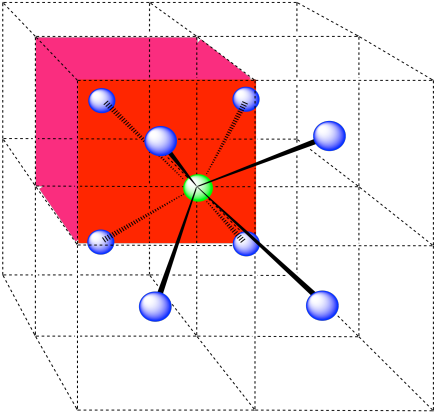
In the picture, consider the green atom coordinated by its nearest neighbors, the blue atoms. One unit cell is highlighted in red.

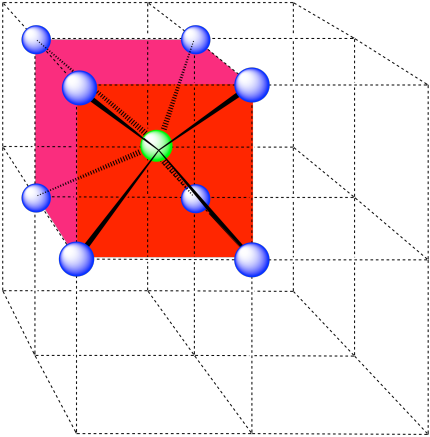
Here is the coordination environment without the surrounding atoms.
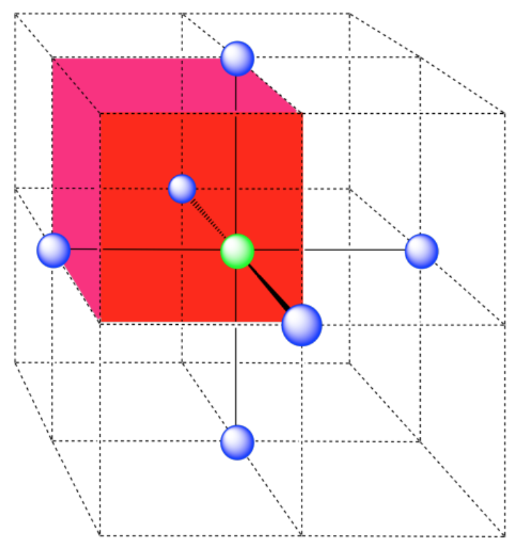
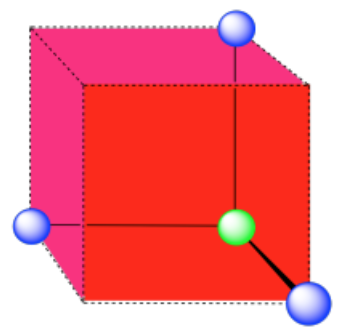
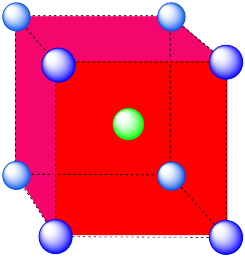
A single unit cell is shown for comparison. The three other nearest atoms are in cells below, behind and to the right of the one shown.
- Answer b:
-
coordination number = 8 (corners of the cube).
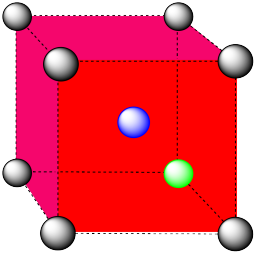
Here is the coordination environment without the surrounding atoms.
A single unit cell is shown below for simplicity. All of the coordinated atoms are found within the cell.
- Answer c:
-
The closest atoms are in the centers of the adjacent cells; the other corners are further away; coordination number = 8.
Here is the coordination environment without the surrounding atoms.
A single unit cell is shown below, for simplicity. Because the atom is in a corner, there are eight other cells arranged around this one: one on the right, two behind, and then four more below.
- Answer d:
-
The closest atoms are on the faces adjacent to the corner position; these faces are found along three planes, with four faces surrounding the corner on each plane; coordination umber = 12.
Here is the coordination environment, without the atoms that are further from the green one.
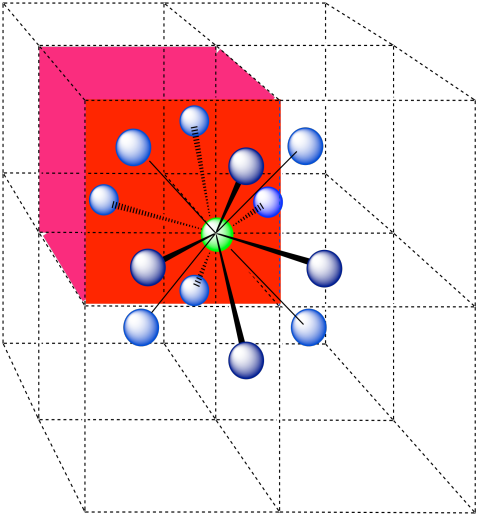
A single unit cell is shown below. Because the atom is in a corner, there are seven other cells arranged around this one: one on the right, two behind, and then four more below.
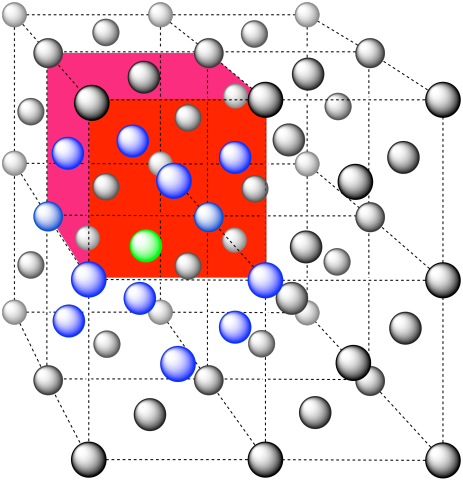
- Answer e:
-
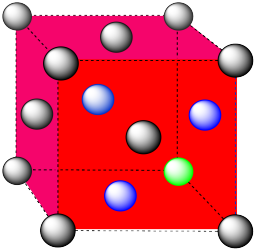
The closest atoms are at the corners around the face (4), as well as the atoms in the middle of each adjacent face (8); coordination number = 12.
Here is the coordination environment without the other atoms.
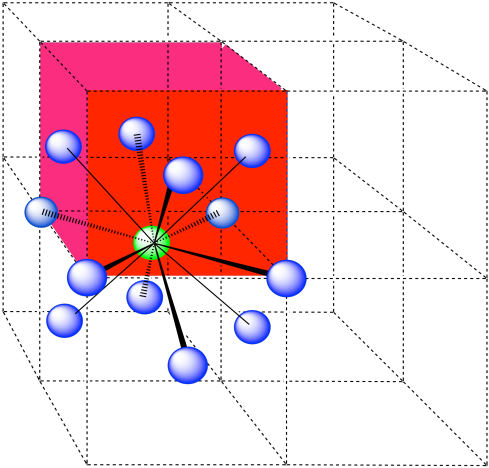
A single unit cell is shown below. There is another cell directly below it.
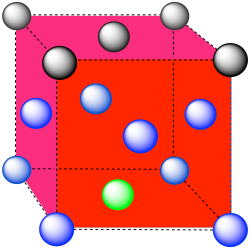
Coordination geometry is related to the coordination number. What is the coordination geometry in each of the following cases?
- an atom at the corner of a simple cubic cell. Remember, it is surrounded by other unit cells, too.
- an atom in the center of a body-centered cubic cell.
- an atom in the corner of a body-centered cubic cell.
- Answer a:
-
Octahedral. An octahedron has six vertices and eight faces.
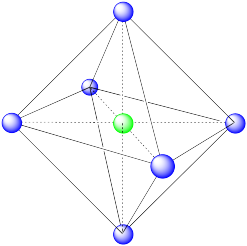
- Answer b:
-
Cubic. A cube has eight vertices and six faces.
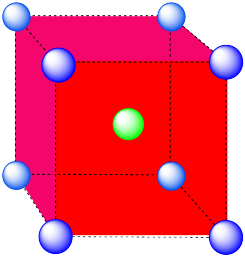
- Answer c:
-
This is also a cube, translated from the last one (i.e. the cube is just shifted to a different position in the lattice).
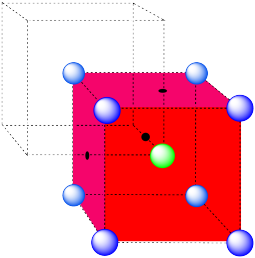
We learned earlier about the holes or interstitial spaces between atoms in a layer. There are also holes between atoms in a three dimensional structure. For example, how would you describe the shape of the holes in the following cases:
- the hole in the middle of a simple cubic cell.
- a hole between the central atom and the face of a body-centered cubic cell.
- the hole right in the middle of the face of a body-centered cubic cell.
- the hole between the atoms forming a valley in one hexagonal layer and the atom sitting in the valley.
- the hole between the atoms forming an empty valley in one hexagonal layer and the atoms in the layer above.
- Answer a:
-
A cubic hole.
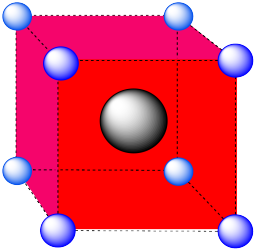
- Answer b:
-
A square pyramidal hole. The atom in the hole is above a square of atoms, with an additional atom right above it.
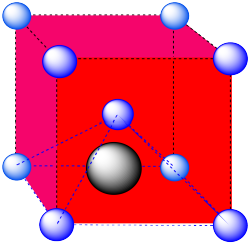
- Answer c:
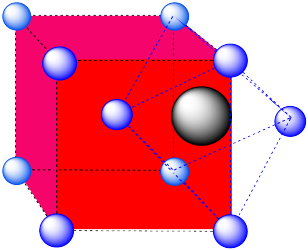
-
An octahedral hole. The atom occupying the hole has been pushed all the way to the face of the cube. It is right in the middle of a square of atoms. One of the vertices is in the center of the next cube.
- Answer d:
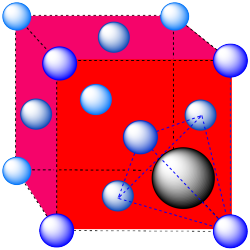
-
A tetrahedral hole. Note that the layers in the cubic closest-packed system run diagonally through the cubic unit cell. The atom in the hole sits above a trio of atoms on three adjacent faces, and is topped by the atom in the corner of the cube. Because a tetrahedron is so symmetric, the arrangement can be described in a number of other ways, choosing any three surrounding atoms as the base and the fourth atom as the cap of the tetrahedron.
- Answer e:
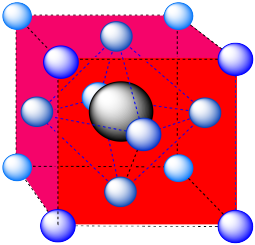
-
An octahedron. Again, the hexagonal layers run diagonally through the unit cell.
Packing efficiency is often determined in terms of the percentage of the volume of a unit cell that is actually occupied by atoms.
In the following cases, calculate the volume of the entire unit cell.
- a simple cubic unit cell.
- a body-centered cubic unit cell.
- a face-centered cubic unit cell.
- a hexagonal close-packed unit cell (remember, this cell is a rhombic prism, not a cube).
You can assume the atoms in the cell are titanium. Titanium has an atomic radius of 2.00 Angstroms (or 2.00 x 10-10 m).
How many atoms are there in a unit cell in the following layers?
- a simple cubic unit cell.
- a body-centered cubic unit cell.
- a face-centered cubic unit cell.
- a hexagonal close-packed unit cell (remember, this cell is a rhombic prism, not a cube).
You may need to add up fractions of titanium atoms to arrive at the answer. The answer may or may not be a whole number.
What is the volume occupied by a titanium atom?
In the following cases, what percentage of the unit cell would be filled with titanium atoms?
- a simple cubic unit cell.
- a body-centered cubic unit cell.
- a face-centered cubic unit cell.
- a hexagonal close-packed unit cell.
The percentage of unit cell that is occupied by atoms is called "the packing efficiency".
Use the appropriate template to draw one unit cell for each of the following metals.
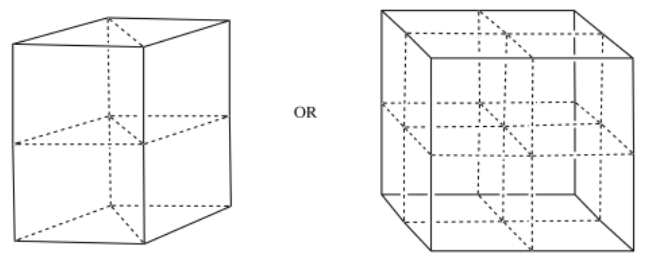
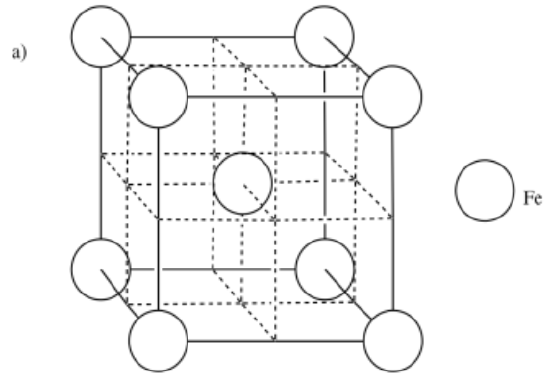
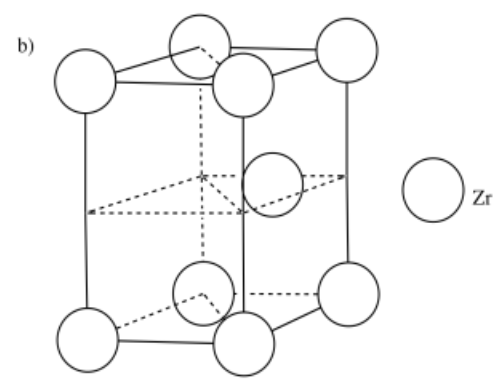
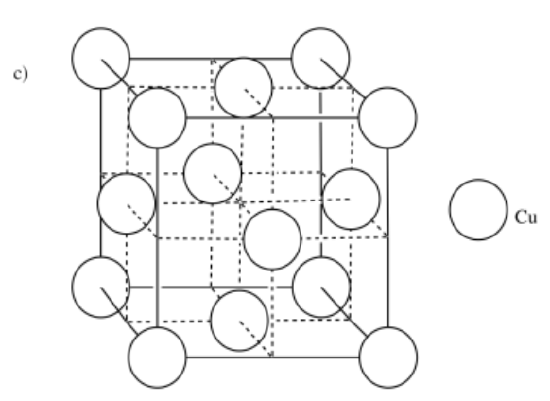
a) iron, Fe, is BCC b) zirconium, Zr, is HCP c) copper, Cu, is FCC
d) manganese, Mn, is BCC e) platinum, Pt, is CCP f) osmium, Os, is HCP
- Answer a:
-
- Answer b:
-
- Answer c:
-
- Answer d:
-
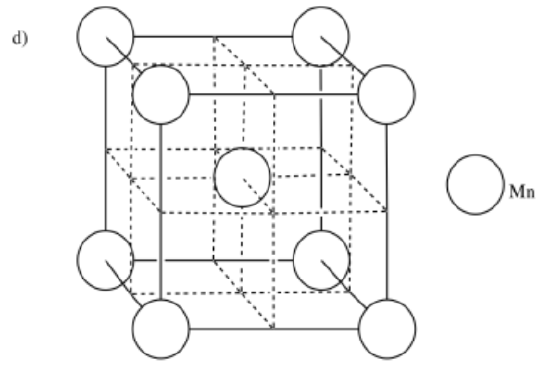
- Answer e:
-
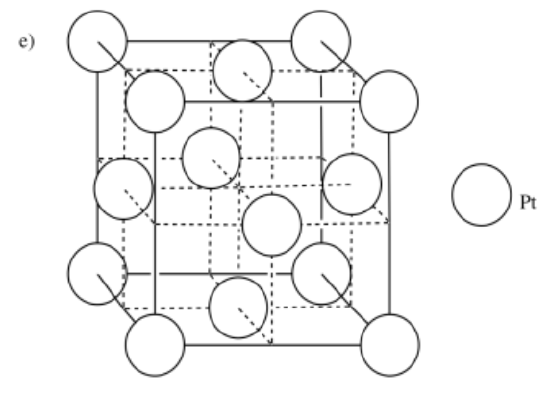
- Answer f:
-
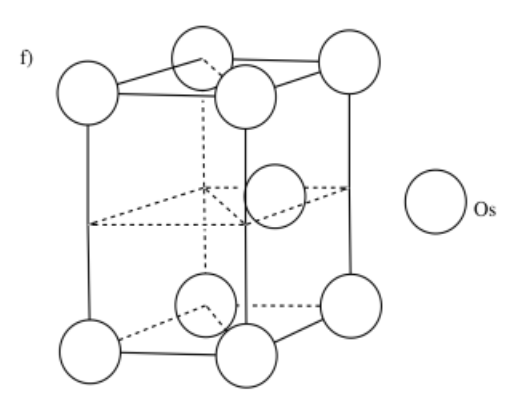
Want to see some additional information? Try these other sites that provide three-dimensional pictures of how atoms pack together.
Kings College Crystal Packing Lab
Naval Research Lab site
Visualization of solid state structures: unit cells, etc.
Oxford University Solid Structures
Visualization of solid state structures: unit cells, etc.


