Molarity
- Page ID
- 54580
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Skills to Develop
- Distinguish the parts of a solution
- Define the units for concentration
Concentration means how much of something there is in a given volume, kind of like density, except that it describes solutions. A solution is some compound, called the solute that is dissolved in another, more abundant compound, called the solvent. To be a solution, the molecules or ions of the solute must be separated from each other and surrounded by solvent molecules or ions. If very small bits of one compound are mixed into another compound, but not actually dissolved into molecules or ions, that is called a suspension (a solid in a liquid) or emulsion (two liquids). In a solution, both the solute and solvent can be any phase, solid, liquid or gas. The concentration of a solution is the amount of solute divided by the total amount of solution, usually. However, there are many different units used for concentration, and some of them assume that there is so much more solvent than solute that you can use amount of solvent instead of amount of solution.
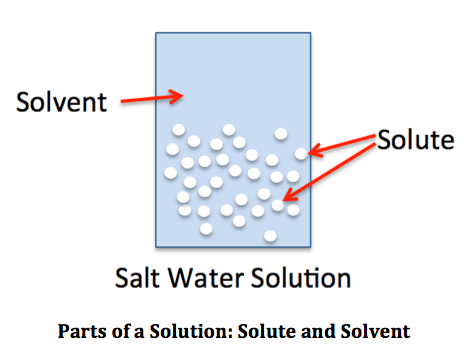
Units for Concentration
There are many, many units used for concentration. Some are mostly used to describe concentrated solutions (that have a lot of solute) and others are mostly used to describe dilute solutions (that have very little solute). The most common unit in chemistry is molarity (abbreviated M), which is moles of solute divided by liters of solution.
\[Molarity=\frac{(moles\; of\; solute)}{(liters\; of\; solution)}\]
For example, if you dissolve 1 mol of NaCl in 1L of water, that is a 1 M (read "1 molar") NaCl solution.
Another common unit is weight %, which means
\[Weight\; (Mass)\; \%=\frac{(mass\; of\; solute)}{(mass\; of\; solution)}\; \times 100\%\]
This is often used for very concentrated solutions. For very dilute solutions, you'll see ppm (parts per million) or ppb (parts per billion):
\[ppm=\frac{(mass\; of\; solute)}{(mass\; of\; solution)}\; \times 10^{6}\]
\[ppb=\frac{(mass\; of\; solute)}{(mass\; of\; solution)}\; \times 10^{9}\]
Many compounds are important even at these very low concentrations. Some chemicals used in agriculture or industry are called "endocrine disrupters" and studies suggest that they can be dangerous for living things at the ppb level. (Example abstract of a scientific paper: note that ppm is described as "high concentration.") In semiconductors, which are what computer chips and LEDs are made of, ppm-level solid solutions enable the essential properties.
Example
HCl (hydrogen chloride) is a really nasty, dangerous gas, but dissolved in water it makes a convenient acid (hydrochloric acid) for many applications in the lab or in industry. When working with an HCl solutions in the lab, we often want to measure the mass of volume of solution used and know how many moles of HCl we added. Unfortunately, when you buy HCl, it usually comes as concentrated HCl, and the bottle will say something like "32% by weight, density 1.1593." Convert this to molarity.
To solve this, we need to think of it like a unit conversion. A good trick for dealing with % quantities is just to translate that into g/g, like this: 32 weight % = (32 g HCl)/(100 g solution). Now we do our usual unit conversion:
\[\left(\dfrac{32\; \cancel{g\; HCl}}{100\; \cancel{g\; solution}}\right) \left(\dfrac{1\; mol\; HCl}{36.46\; \cancel{g\; HCl}}\right) \left(\dfrac{1.1593\; \cancel{g}}{1\; \cancel{mL\; solution}}\right) \left(\dfrac{\cancel{1000\; mL}}{1\; L}\right)=10\; M\; HCl\]
Here we started with units of g HCl/g solution, and converted the g HCl to moles, and the g solution to liters using the density, which is (g/ml). Notice that the number of significant figures is fairly low. This is because the gas HCl can evaporate out of the solution, just like the water, so the concentration might change a little over time. If you want to know the concentration more precisely, see the next section on titrations to find out how to measure it.
Now suppose you want to make 2.5 M HCl using the 10 M HCl. You will need to dilute it, which means adding solvent to decrease the concentration. If you want to make 1 L of 2.5 M HCl, how much 10 M HCl do you dilute?
To solve this, we can still think about it like a unit conversion. We want 1 L of 2.5 M HCl solution. In the first step, we will convert to the number of moles of HCl needed to make that solution. In the second step, we will find how many ml of 10 M solution have this number of moles HCl.
\[(1\; \cancel{L\; of\; 2.5\; M\; HCl}) \left(\dfrac{2.5\; \cancel{mol\; HCl}}{1\; \cancel{L\; of\; 2.5\; M\; HCl}}\right) \left(\dfrac{1000\; mL\; of\; 10\; M\; HCl}{10\; \cancel{mol\; HCl}}\right)=250\; mL\; of\; 10\; M\; HCl\]
To make the solution, we will take 250 mL of 10 M HCl, and we will put it in a 1 L volumetric flask, and then add water slowly, with mixing, until the volume reaches the 1 L mark. The reason we do it this way, instead of just adding 750 mL of water, is that the density can change because of the solute. If we use the volumetric flask, we can be sure that we have exactly 2.5 mol HCl in exactly 1 L of solution.
Contributors and Attributions
Emily V Eames (City College of San Francisco)