8.2: Ionic Bonding
- Page ID
- 349435
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To quantitatively describe the energetic factors involved in the formation of an ionic bond
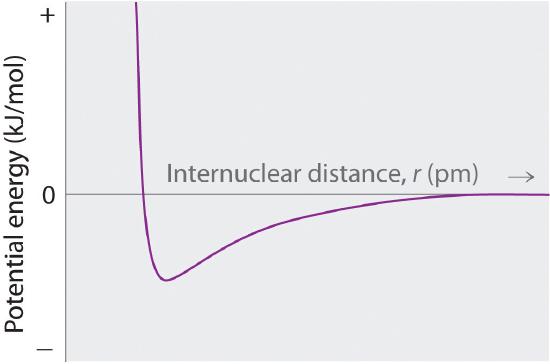
Ionic bonds are formed when positively and negatively charged ions are held together by electrostatic forces. The energy of the electrostatic attraction (E), a measure of the force’s strength, is inversely proportional to the internuclear distance between the charged particles (r):
\(E \propto \dfrac{Q_{1}Q_{2}}{r}\quad \quad E = k\dfrac{Q_{1}Q_{2}}{r} \tag{4.1.1} \)
where each ion’s charge is represented by the symbol Q. The proportionality constant k is equal to 2.31 × 10−28 J·m.This value of k includes the charge of a single electron (1.6022 × 10−19 C) for each ion. The equation can also be written using the charge of each ion, expressed in coulombs (C), incorporated in the constant. In this case, the proportionality constant, k, equals 8.999 × 109 J·m/C2. In the example given, Q1 = +1(1.6022 × 10−19 C) and Q2 = −1(1.6022 × 10−19 C). If Q1 and Q2 have opposite signs (as in NaCl, for example, where Q1 is +1 for Na+ and Q2 is −1 for Cl−), then E is negative, which means that energy is released when oppositely charged ions are brought together from an infinite distance to form an isolated ion pair.

For ions of opposite charge attraction increases as the charge increases and decreases as the distance between the ions increases
As shown by the green curve in the lower half of Figure 4.1.2 predicts that the maximum energy is released when the ions are infinitely close to each other, at r = 0. Because ions occupy space and have a structure with the positive nucleus being surrounded by electrons, however, they cannot be infinitely close together. At very short distances, repulsive electron–electron interactions between electrons on adjacent ions become stronger than the attractive interactions between ions with opposite charges, as shown by the red curve in the upper half of Figure 4.1.2. The total energy of the system is a balance between the attractive and repulsive interactions. The purple curve in Figure 4.1.2 shows that the total energy of the system reaches a minimum at r0, the point where the electrostatic repulsions and attractions are exactly balanced. This distance is the same as the experimentally measured bond distance.
Note the Pattern
Energy is released when a bond is formed.
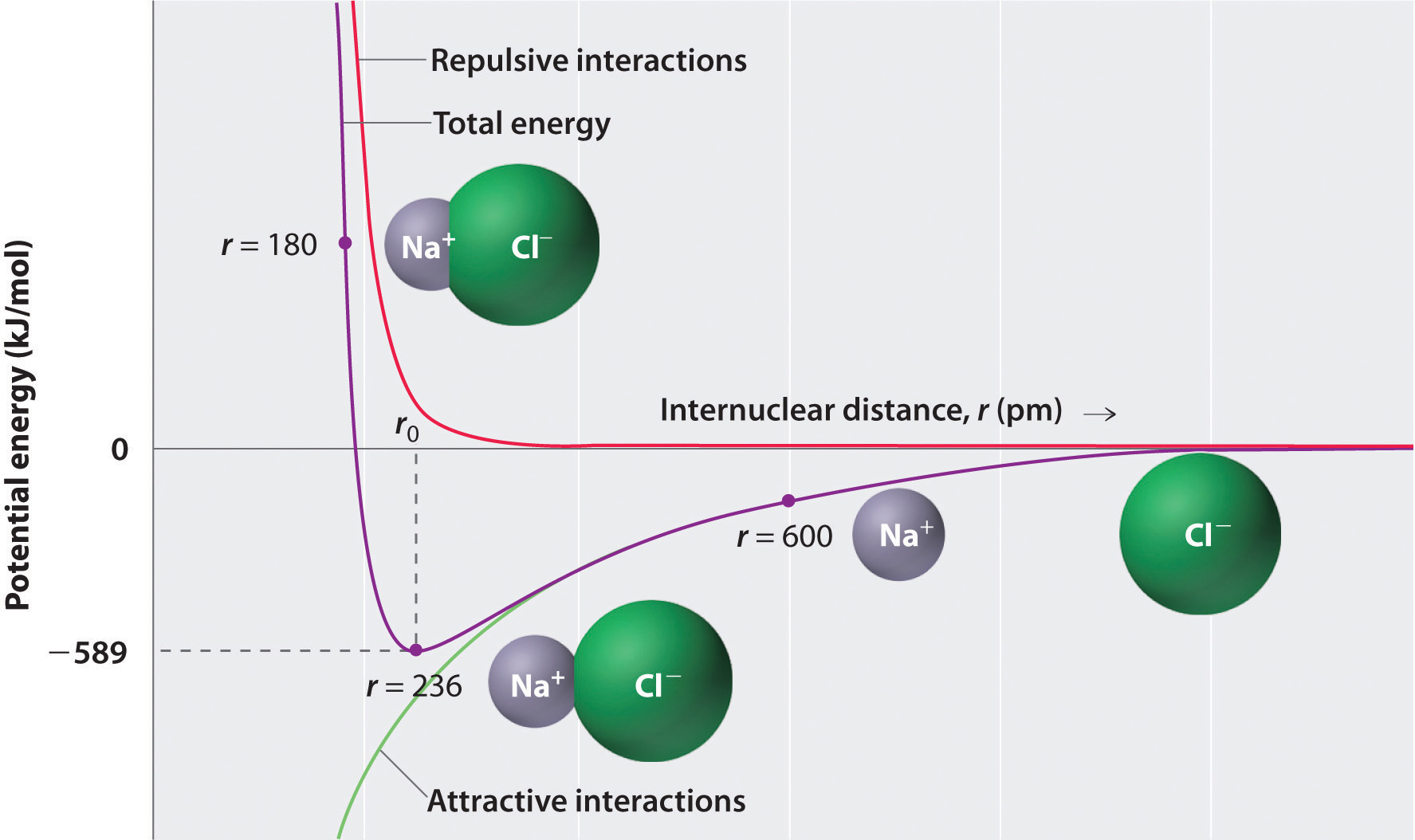
Let’s consider the energy released when a gaseous Na+ ion and a gaseous Cl− ion are brought together from r = ∞ to r = r0. Given that the observed gas-phase internuclear distance is 236 pm, the energy change associated with the formation of an ion pair from an Na+(g) ion and a Cl−(g) ion is as follows:
\( E = k\dfrac{Q_{1}Q_{2}}{r_{0}} = (2.31 \times {10^{ - 28}}\rm{J}\cdot \cancel{m} ) \left( \dfrac{( + 1)( - 1)}{236\; \cancel{pm} \times 10^{ - 12} \cancel{m/pm}} \right) = - 9.79 \times 10^{ - 19}\; J/ion\; pair \tag{4.1.2} \)
The negative value indicates that energy is released. Our convention is that if a chemcal process provides energy to the outside world, the energy change is negative. If it requires energy, the energy change is positive, energy has to be given to the atoms. To calculate the energy change in the formation of a mole of NaCl pairs, we need to multiply the energy per ion pair by Avogadro’s number:
\( E=\left ( -9.79 \times 10^{ - 19}\; J/ \cancel{ion pair} \right )\left ( 6.022 \times 10^{ 23}\; \cancel{ion\; pair}/mol\right )=-589\; kJ/mol \tag{4.1.3} \)
This is the energy released when 1 mol of gaseous ion pairs is formed, not when 1 mol of positive and negative ions condenses to form a crystalline lattice. Because of long-range interactions in the lattice structure, this energy does not correspond directly to the lattice energy of the crystalline solid. However, the large negative value indicates that bringing positive and negative ions together is energetically very favorable, whether an ion pair or a crystalline lattice is formed.
We summarize the important points about ionic bonding:
- At r0, the ions are more stable (have a lower potential energy) than they are at an infinite internuclear distance. When oppositely charged ions are brought together from r = ∞ to r = r0, the energy of the system is lowered (energy is released).
- Because of the low potential energy at r0, energy must be added to the system to separate the ions. The amount of energy needed is the bond energy.
- The energy of the system reaches a minimum at a particular internuclear distance (the bond distance).
Ionic Crystal Lattices
An ionic solid is formed out of endlessly repeating patterns of ionic pairs. Because we want to establish the basics about ionic bonding and not get involved in detail we will continue to use table salt, NaCl, to discuss ionic bonding.
In NaCl, of course, an electron is transferred from each sodium atom to a chlorine atom leaving Na+ and Cl-. The size of the lattice depends on the physical size of the crystal which can be microscopic, a few nm on a side to macroscopic, centimeters or even more. Salt crystals that you buy at the store can range in size from a few tenths of a mm in finely ground table salt to a few mm for coarsely ground salt used in cooking. Given that the spacing between the Na+ and Cl- ions, is ~240 pm, a 2.4 mm on edge crystal has 10+7 Na+ - Cl- units, and a cube of salt 2mm on edge will have about 2 x 1021 atoms.
The ions arrange themselves into an extended lattice. The distinguishing feature of these lattices is that they are space filling, there are no voids. Thinking about this in three dimensions this turns out to be a bit complex. In nature, there are only 14 such lattices, called Bravais lattices after August Bravais who first classified them in 1850. If interested, you can view a video visualization of the 14 lattices by Manuel Moreira Baptista

Remember that the Na+ ions, shown here in purple, will be much smaller than Na atoms, and Cl- ions will be much larger than Cl atoms. The repeating pattern is called the unit cell.

Figure 4.1.4The unit cell for an NaCl crystal lattice. If you look at the diagram carefully, you will see that the sodium ions and chloride ions alternate with each other in each of the three dimensions.
This diagram is easy enough to draw with a computer, but extremely difficult to draw convincingly by hand. We normally draw an "exploded" version which looks like this:

By chance we might just as well have centered the diagram around a chloride ion - that, of course, would be touched by 6 sodium ions. Sodium chloride is described as being 6:6-coordinated. This diagram represents only a tiny part of the whole sodium chloride crystal; the pattern repeats in this way over countless ions.
Sodium chloride has a high melting and boiling point
There are strong electrostatic attractions between the positive and negative ions, and it takes a lot of heat energy to overcome them. Ionic substances all have high melting and boiling points. Differences between ionic substances will depend on things like:
- The number of charges on the ions: Magnesium oxide has exactly the same structure as sodium chloride, but a much higher melting and boiling point. The 2+ and 2- ions attract each other more strongly than 1+ attracts 1-.
- The sizes of the ions: If the ions are smaller they get closer together and so the electrostatic attractions are greater. Rubidium iodide, for example, melts and boils at slightly lower temperatures than sodium chloride, because both rubidium and iodide ions are bigger than sodium and chloride ions. The attractions are less between the bigger ions and so less heat energy is needed to separate them.
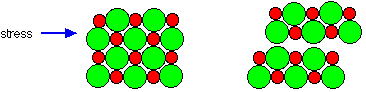
Sodium chloride crystals are brittle
Brittleness is again typical of ionic substances. Imagine what happens to the crystal if a stress is applied which shifts the ion layers slightly.
The electrical behavior of sodium chloride
Solid sodium chloride does not conduct electricity, because there are no electrons which are free to move. When it melts, at a very high temperature of course, the sodium and chloride ions can move freely when a voltage is placed across the liquid. The positive sodium ions move towards the negatively charged electrode (the cathode). When they get there, each sodium ion picks up an electron from the electrode to form a sodium atom. These float to the top of the melt as molten sodium metal. (And assuming you are doing this open to the air, this immediately catches fire and burns with an orange flame.)
The power source (the battery or whatever) moves electrons along the wire in the external circuit so that the number of electrons is the same. That flow of electrons would be seen as an electric current (the external circuit is all the rest of the circuit apart from the molten sodium chloride.) Thus, in the process called electrolysis, sodium and chlorine are produced. This is a chemical change rather than a physical process.
\[Na^++e^-\rightarrow Na \notag \]
Meanwhile, chloride ions are attracted to the positive electrode (the anode). When they get there, each chloride ion loses an electron to the anode to form an atom. These then pair up to make chlorine molecules. Chlorine gas is produced. Overall, the change is . . .
\[2Cl^− \rightarrow Cl)2+2e^− \notag \]
The new electrons deposited on the anode are pumped off around the external circuit by the power source, eventually ending up on the cathode where they will be transferred to sodium ions. Molten sodium chloride conducts electricity because of the movement of the ions in the melt, and the discharge of the ions at the electrodes. Both of these have to happen if you are to get electrons flowing in the external circuit. In solid sodium chloride, of course, that ion movement can not happen and that stops any possibility of any current flow in the circuit.
Acknowlegement: The discussion of the NaCl lattice is a slightly modified version of the Jim Clark's article on the ChemWiki
Example 1
Calculate the amount of energy released when 1 mol of gaseous Li+F− ion pairs is formed from the separated ions. The observed internuclear distance in the gas phase is 156 pm.
Given: cation and anion, amount, and internuclear distance
Asked for: energy released from formation of gaseous ion pairs
Strategy:
Substitute the appropriate values into Equation 4.1.1 to obtain the energy released in the formation of a single ion pair and then multiply this value by Avogadro’s number to obtain the energy released per mole.
Solution:
Inserting the values for Li+F− into Equation 4.1.1 (where Q1 = +1, Q2 = −1, and r = 156 pm), we find that the energy associated with the formation of a single pair of Li+F− ions is
\( E = k\dfrac{Q_{1}Q_{2}}{r_{0}} = (2.31 \times {10^{ - 28}}\rm{J}\cdot \cancel{m}) \left( \dfrac{( + 1)( - 1)}{156\; \cancel{pm} \times 10^{ - 12} \cancel{m/pm}} \right) = - 1.48 \times 10^{ - 18}\; J/ion\; pair \)
Then the energy released per mole of Li+F− ion pairs is
\( E=\left ( -1.48 \times 10^{ - 18}\; J/ \cancel{ion pair} \right )\left ( 6.022 \times 10^{ 23}\; \cancel{ion\; pair}/mol\right )=-891\; kJ/mol \)
Because Li+ and F− are smaller than Na+ and Cl− (see Figure 3.2.7 ), the internuclear distance in LiF is shorter than in NaCl. Consequently, in accordance with Equation 4.1.1, much more energy is released when 1 mol of gaseous Li+F− ion pairs is formed (−891 kJ/mol) than when 1 mol of gaseous Na+Cl− ion pairs is formed (−589 kJ/mol).
Exercise
Calculate the amount of energy released when 1 mol of gaseous MgO ion pairs is formed from the separated ions. The internuclear distance in the gas phase is 175 pm.
Answer: −3180 kJ/mol = −3.18 × 103 kJ/mol
Summary
The strength of the electrostatic attraction between ions with opposite charges is directly proportional to the magnitude of the charges on the ions and inversely proportional to the internuclear distance. The total energy of the system is a balance between the repulsive interactions between electrons on adjacent ions and the attractive interactions between ions with opposite charges.
Ionic compounds usually form hard crystalline solids that melt at rather high temperatures and are very resistant to evaporation. They can be easily cleaved. When the dissolve in aqueous solution, the ions make the solution a good conductor of electricity. These properties stem from the characteristic internal structure of an ionic solid, illustrated schematically in part (a) in Figure 4.1.5 , which shows the three-dimensional array of alternating positive and negative ions held together by strong electrostatic attractions.
Key Takeaway
- The amount of energy needed to separate a gaseous ion pair is its bond energy.
Conceptual Problems
-
Describe the differences in behavior between NaOH and CH3OH in aqueous solution. Which solution would be a better conductor of electricity? Explain your reasoning.
-
What is the relationship between the strength of the electrostatic attraction between oppositely charged ions and the distance between the ions? How does the strength of the electrostatic interactions change as the size of the ions increases?
-
Which will result in the release of more energy: the interaction of a gaseous sodium ion with a gaseous oxide ion or the interaction of a gaseous sodium ion with a gaseous bromide ion? Why?
-
Which will result in the release of more energy: the interaction of a gaseous chloride ion with a gaseous sodium ion or a gaseous potassium ion? Explain your answer.
-
What are the predominant interactions when oppositely charged ions are
- far apart?
- at internuclear distances close to r0?
- very close together (at a distance that is less than the sum of the ionic radii)?
-
Several factors contribute to the stability of ionic compounds. Describe one type of interaction that destabilizes ionic compounds. Describe the interactions that stabilize ionic compounds.
-
What is the relationship between the electrostatic attractive energy between charged particles and the distance between the particles?
Answer
-
The interaction of a sodium ion and an oxide ion. The electrostatic attraction energy between ions of opposite charge is directly proportional to the charge on each ion (Q1 and Q2 in Equation 4.1.1). Thus, more energy is released as the charge on the ions increases (assuming the internuclear distance does not increase substantially). A sodium ion has a +1 charge; an oxide ion, a −2 charge; and a bromide ion, a −1 charge. For the interaction of a sodium ion with an oxide ion, Q1 = +1 and Q2 = −2, whereas for the interaction of a sodium ion with a bromide ion, Q1 = +1 and Q2 = −1. The larger value of Q1 × Q2 for the sodium ion–oxide ion interaction means it will release more energy.
Numerical Problems
-
How does the energy of the electrostatic interaction between ions with charges +1 and −1 compare to the interaction between ions with charges +3 and −1 if the distance between the ions is the same in both cases? How does this compare with the magnitude of the interaction between ions with +3 and −3 charges?
-
How many grams of gaseous MgCl2 are needed to give the same electrostatic attractive energy as 0.5 mol of gaseous LiCl? The ionic radii are Li+ = 76 pm, Mg+2 = 72 pm, and Cl− = 181 pm.
-
Sketch a diagram showing the relationship between potential energy and internuclear distance (from r = ∞ to r = 0) for the interaction of a bromide ion and a potassium ion to form gaseous KBr. Explain why the energy of the system increases as the distance between the ions decreases from r = r0 to r = 0.
-
Calculate the magnitude of the electrostatic attractive energy (E, in kilojoules) for 85.0 g of gaseous SrS ion pairs. The observed internuclear distance in the gas phase is 244.05 pm.
-
What is the electrostatic attractive energy (E, in kilojoules) for 130 g of gaseous HgI2? The internuclear distance is 255.3 pm.
Answers
-
According to Equation 4.1.1, in the first case Q1Q2 = (+1)(−1) = −1; in the second case, Q1Q2 = (+3)(−1) = −3. Thus, E will be three times larger for the +3/−1 ions. For +3/−3 ions, Q1Q2 = (+3)(−3) = −9, so E will be nine times larger than for the +1/−1 ions.