Ionic Structures
- Page ID
- 3627
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This page explains the relationship between the arrangement of the ions in a typical ionic solid like sodium chloride and its physical properties - melting point, boiling point, brittleness, solubility and electrical behavior. It also explains why cesium chloride has a different structure from sodium chloride even though sodium and cesium are both in Group 1 of the Periodic Table.
The structure of a typical ionic solid - sodium chloride
Sodium chloride is taken as a typical ionic compound. Compounds like this consist of a giant (endlessly repeating) lattice of ions. So sodium chloride (and any other ionic compound) is described as having a giant ionic structure.
You should be clear that giant in this context does not just mean very large. It means that you can't state exactly how many ions there are. There could be billions of sodium ions and chloride ions packed together, or trillions, or whatever - it simply depends how big the crystal is. That is different from, say, a water molecule which always contains exactly 2 hydrogen atoms and one oxygen atom - never more and never less. A small representative bit of a sodium chloride lattice looks like this:
If you look at the diagram carefully, you will see that the sodium ions and chloride ions alternate with each other in each of the three dimensions. This diagram is easy enough to draw with a computer, but extremely difficult to draw convincingly by hand. We normally draw an "exploded" version which looks like this:
Only those ions joined by lines are actually touching each other. The sodium ion in the center is being touched by 6 chloride ions. By chance we might just as well have centered the diagram around a chloride ion - that, of course, would be touched by 6 sodium ions. Sodium chloride is described as being 6:6-coordinated. This diagram represents only a tiny part of the whole sodium chloride crystal; the pattern repeats in this way over countless ions.
How to draw this structure
Draw a perfect square:
Now draw an identical square behind this one and offset a bit. You might have to practice a bit to get the placement of the two squares right. If you get it wrong, the ions get all tangled up with each other in your final diagram.
Turn this into a perfect cube by joining the squares together:
Now the tricky bit! Subdivide this big cube into 8 small cubes by joining the mid point of each edge to the mid point of the edge opposite it. To complete the process you will also have to join the mid point of each face (easily found once you've joined the edges) to the mid point of the opposite face.
Now all you have to do is put the ions in. Use different colors or different sizes for the two different ions, and don't forget a key. It does not matter whether you end up with a sodium ion or a chloride ion in the center of the cube - all that matters is that they alternate in all three dimensions.
You should be able to draw a perfectly adequate free-hand sketch of this in under two minutes - less than one minute if you're not too fussy!
Why is sodium chloride 6:6-coordinated?
The more attraction there is between the positive and negative ions, the more energy is released. The more energy that is released, the more energetically stable the structure becomes. That means that to gain maximum stability, you need the maximum number of attractions. So why does each ion surround itself with 6 ions of the opposite charge? That represents the maximum number of chloride ions that you can fit around a central sodium ion before the chloride ions start touching each other. If they start touching, you introduce repulsions into the crystal which makes it less stable.
The different structure of cesium chloride
We'll look first at the arrangement of the ions and then talk about why the structures of sodium chloride and cesium chloride are different afterwards. Imagine a layer of chloride ions as shown below. The individual chloride ions aren't touching each other. That's really important - if they were touching, there would be repulsion.

Now let's place a similarly arranged layer of cesium ions on top of these.
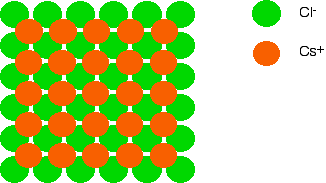
Notice that the cesium ions aren't touching each other either, but that each cesium ion is resting on four chloride ions from the layer below.
Now let's put another layer of chloride ions on, exactly the same as the first layer. Again, the chloride ions in this layer are NOT touching those in the bottom layer - otherwise you are introducing repulsion. Since we are looking directly down on the structure, you can't see the bottom layer of chloride ions any more, of course.
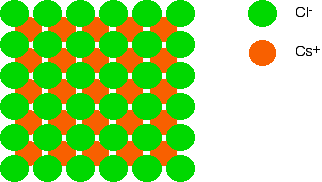
If you now think about a cesium ion sandwiched between the two layers of chloride ions, it is touching four chloride ions in the bottom layer, and another four in the top one. Each cesium ion is touched by eight chloride ions. We say that it is 8-coordinated. If we added another layer of cesium ions, you could similarly work out that each chloride ion was touching eight cesium ions. The chloride ions are also 8-coordinated. Overall, then, cesium chloride is 8:8-coordinated.
The final diagram in this sequence takes a slightly tilted view of the structure so that you can see how the layers build up. These diagrams are quite difficult to draw without it looking as if ions of the same charge are touching each other. They aren't!
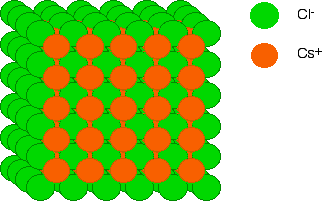
Diagrams of ionic crystals are usually simplified to show the most basic unit of the repeating pattern. For cesium chloride, you could, for example, draw a simple diagram showing the arrangement of the chloride ions around each cesium ion:
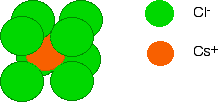
By reversing the colors (green chloride ion in the center, and orange cesium ions surrounding it), you would have an exactly equivalent diagram for the arrangement of cesium ions around each chloride ion.
Why are the cesium chloride and sodium chloride structures different?
When attractions are set up between two ions of opposite charges, energy is released. The more energy that can be released, the more stable the system becomes. That means that the more contact there is between negative and positive ions, the more stable the crystal should become.
If you can surround a positive ion like cesium with eight chloride ions rather than just six (and vice versa for the chloride ions), then you should have a more stable crystal. So why does not sodium chloride do the same thing? Look again at the last diagram:

Now imagine what would happen if you replaced the cesium ion with the smaller sodium ion. Sodium ions are, of course, smaller than cesium ions because they have fewer layers of electrons around them.
You still have to keep the chloride ions in contact with the sodium. The effect of this would be that the whole arrangement would shrink, bringing the chloride ions into contact with each other - and that introduces repulsion.
Any gain in attractions because you have eight chlorides around the sodium rather than six is more than countered by the new repulsions between the chloride ions themselves. When sodium chloride is 6:6-coordinated, there are no such repulsions - and so that is the best way for it to organize itself.
Which structure a simple 1:1 compound like NaCl or CsCl crystallizes in depends on the radius ratio of the positive and the negative ions. If the radius of the positive ion is bigger than 73% of that of the negative ion, then 8:8-coordination is possible. Less than that (down to 41%) then you get 6:6-coordination.
In CsCl, the cesium ion is about 93% of the size of the chloride ion - so is easily within the range where 8:8-coordination is possible. But with NaCl, the sodium ion is only about 52% of the size of the chloride ion. That puts it in the range where you get 6:6-coordination.
The physical properties of sodium chloride
Sodium chloride is taken as typical of ionic compounds, and is chosen rather than, say, cesium chloride, because it is found on every syllabus at this level.
Sodium chloride has a high melting and boiling point
There are strong electrostatic attractions between the positive and negative ions, and it takes a lot of heat energy to overcome them. Ionic substances all have high melting and boiling points. Differences between ionic substances will depend on things like:
- The number of charges on the ions: Magnesium oxide has exactly the same structure as sodium chloride, but a much higher melting and boiling point. The 2+ and 2- ions attract each other more strongly than 1+ attracts 1-.
- The sizes of the ions: If the ions are smaller they get closer together and so the electrostatic attractions are greater. Rubidium iodide, for example, melts and boils at slightly lower temperatures than sodium chloride, because both rubidium and iodide ions are bigger than sodium and chloride ions. The attractions are less between the bigger ions and so less heat energy is needed to separate them.
Sodium chloride crystals are brittle
Brittleness is again typical of ionic substances. Imagine what happens to the crystal if a stress is applied which shifts the ion layers slightly.
Ions of the same charge are brought side-by-side and so the crystal repels itself to pieces!
Sodium chloride is soluble in water
Many ionic solids are soluble in water - although not all. It depends on whether there are big enough attractions between the water molecules and the ions to overcome the attractions between the ions themselves. Positive ions are attracted to the lone pairs on water molecules and co-ordinate (dative covalent) bonds may form. Water molecules form hydrogen bonds with negative ions.
Sodium chloride is insoluble in organic solvents
This is also typical of ionic solids. The attractions between the solvent molecules and the ions are not big enough to overcome the attractions holding the crystal together.
The electrical behavior of sodium chloride
Solid sodium chloride does not conduct electricity, because there are no electrons which are free to move. When it melts, sodium chloride undergoes electrolysis, which involves conduction of electricity because of the movement and discharge of the ions. In the process, sodium and chlorine are produced. This is a chemical change rather than a physical process.
The positive sodium ions move towards the negatively charged electrode (the cathode). When they get there, each sodium ion picks up an electron from the electrode to form a sodium atom. These float to the top of the melt as molten sodium metal. (And assuming you are doing this open to the air, this immediately catches fire and burns with an orange flame.)
\[ Na^+ + e^- \rightarrow Na \nonumber \]
The movement of electrons from the cathode onto the sodium ions leaves spaces on the cathode. The power source (the battery or whatever) moves electrons along the wire in the external circuit to fill those spaces. That flow of electrons would be seen as an electric current (the external circuit is all the rest of the circuit apart from the molten sodium chloride.)
Meanwhile, chloride ions are attracted to the positive electrode (the anode). When they get there, each chloride ion loses an electron to the anode to form an atom. These then pair up to make chlorine molecules. Chlorine gas is produced. Overall, the change is . . .
\[ 2Cl^- \rightarrow Cl_2 + 2e^- \nonumber \]
The new electrons deposited on the anode are pumped off around the external circuit by the power source, eventually ending up on the cathode where they will be transferred to sodium ions. Molten sodium chloride conducts electricity because of the movement of the ions in the melt, and the discharge of the ions at the electrodes. Both of these have to happen if you are to get electrons flowing in the external circuit. In solid sodium chloride, of course, that ion movement ca not happen and that stops any possibility of any current flow in the circuit.
Contributors
Jim Clark (Chemguide.co.uk)


