17.3: Collision and activation- the Arrhenius law
- Page ID
- 46070
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Make sure you thoroughly understand the following essential ideas which have been presented above. It is especially imortant that you know the precise meanings of all the green-highlighted terms in the context of this topic.
- Explain the meaning of a reaction mechanism and define elementary step and intermediate.
- Describe the role of collisions in reaction mechanisms, and explain why not all collisions lead to the formation of products.
- Sketch out activation energy diagrams for simple reactions that are endothermic or exothermic,
- Explain how an activated complex differs from an intermediate.
- Define catalyst, and sketch out an activation energy diagram that illustrates how catalysts work.
- Explain the significance of the various terms that appear in the Arrhenius Law.
- Sketch out a typical Arrhenius Law plot for a hypothetical reaction at higher and lower temperatures.
- Explain how the activation energy of a reaction can be determined experimentally.
- Explain the significance of the various terms that appear in the pre-exponential factor of the Arrhenius equation.
Why are some reactions so much faster than others, and why are reaction rates independent of the thermodynamic tendency of the reaction to take place? These are the central questions we address in this unit. In doing so, we open the door to the important topic of reaction mechanisms: what happens at the microscopic level when chemical reactions take place? We can thank Prof. Svante Arrhenius for unlocking this door! To keep things as simple as possible, we will restrict ourselves to reactions that take place in the gas phase.The same principles will apply to reactions in liquids and solids, but with added complications that we will discuss in a later unit.
Reaction mechanisms
The mechanism of a chemical reaction is the sequence of actual events that take place as reactant molecules are converted into products. Each of these events constitutes an elementary step that can be represented as a coming-together of discrete particles ("collison") or as the breaking-up of a molecule ("dissociation") into simpler units. The molecular entity that emerges from each step may be a final product of the reaction, or it might be an intermediate — a species that is created in one elementary step and destroyed in a subsequent step, and therefore does not appear in the net reaction equation.
A reaction mechanism must ultimately be understood as a "blow-by-blow" description of the molecular-level events whose sequence leads from reactants to products. These elementary steps (also called elementary reactions) are almost always very simple ones involving one, two, or [rarely] three chemical species which are classified, respectively, as
| unimolecular | A → | by far the most common |
| bimolecular | A + B → | |
| termolecular | A + B + C → | very rare |
Collision theory of chemical change: Molecules must collide before they can react
This fundamental rule must guide any analysis of an ordinary chemical reaction mechanism.

This explains why termolecular processes are so uncommon. The kinetic theory of gases tells us that for every 1000 binary collisions, there will be only one event in which three molecules simultaneously come together. Four-way collisions are so improbable that this process has never been demonstrated in an elementary reaction. Consider a simple bimolecular step
\[\ce{A + B -> products} \nonumber\]
Clearly, if two molecules A and B are to react, they must approach closely enough to disrupt some of their existing bonds and to permit the creation of any new ones that are needed in the products. We call such an encounter a collision.
The frequency of collisions between A and B in a gas will be proportional to the concentration of each; if we double [A], the frequency of A-B collisions will double, and doubling [B] will have the same effect. So if all collisions lead to products, than the rate of a bimolecular process will be first-order in A and B, or second-order overall:
\[\text{rate} = k[\ce{A}][\ce{B}] \nonumber\]
However, not all collisions are equal. In a gas at room temperature and normal atmospheric pressure, there will be about 1033 collisions in each cubic centimetre every second. If every collision between two reactant molecules yielded products, all reactions would be complete in a fraction of a second.
When two billiard balls collide, they simply bounce off of each other. This is also the most likely outcome if the reaction between A and B requires a significant disruption or rearrangement of the bonds between their atoms. In order to effectively initiate a reaction, collisions must be sufficiently energetic (kinetic energy) to bring about this bond disruption. More about this further on.

And there is often one additional requirement. In many reactions, especially those involving more complex molecules, the reacting species must be oriented in a manner that is appropriate for the particular process. For example, in the gas-phase reaction of dinitrogen oxide with nitric oxide, the oxygen end of N2O must hit the nitrogen end of NO; reversing the orientation of either molecule prevents the reaction.
Owing to the extensive randomization of molecular motions in a gas or liquid, there are always enough correctly-oriented molecules for some of the molecules to react. But of course, the more critical this orientational requirement is, the fewer collisions will be effective.
Anatomy of a collision
Energetic collisions between molecules cause interatomic bonds to stretch and bend farther, temporarily weakening them so that they become more susceptible to cleavage. Distortion of the bonds can expose their associated electron clouds to interactions with other reactants that might lead to the formation of new bonds. Chemical bonds have some of the properties of mechanical springs, whose potential energy depends on the extent to which they are stretched or compressed. Each atom-to-atom bond can be described by a potential energy diagram that shows how its energy changes with its length. When the bond absorbs energy (either from heating or through a collision), it is elevated to a higher quantized vibrational state (indicated by the horizontal lines) that weakens the bond as its length oscillates between the extended limits corresponding to the curve.
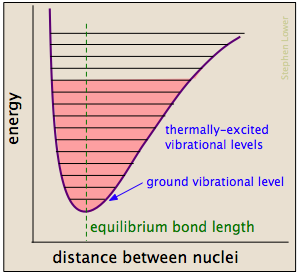
A particular collision will typically excite a number of bonds in this way. Within about 10–13 second this excitation gets distributed among the other bonds in the molecule in rather complex and unpredictable ways that can concentrate the added energy at a particularly vulnerable point. The affected bond can stretch and bend farther, making it more susceptible to cleavage. Even if the bond does not break by pure stretching, it can become distorted or twisted so as to expose nearby electron clouds to interactions with other reactants that might encourage a reaction.
Consider, for example, the isomerization of cyclopropane to propene which takes place at fairly high temperatures in the gas phase.

We can imagine the collision-to-product sequence in the following [grossly oversimplified] way:
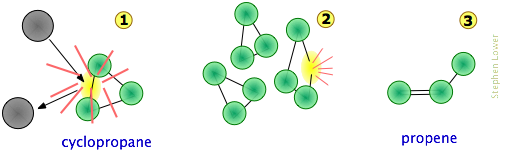
Note that
- To keep things simple, we do not show the hydrogen atoms here. This is reasonable because C–C bonds are weaker then C–H bonds and thus less likely to be affected.
- The collision at
will usually be with another cyclopropane molecule, but because no part of the colliding molecule gets incorporated into the product, it can in principle be a noble gas or some other non-reacting species;
- Although the C–C bonds in cyclopropane are all identicial, the instantaneous localization of the collisional energy can distort the molecule in various ways (
), leading to a configuration sufficiently unstable to initiate the rearrangement to the product.
The cyclopropane isomerization described above is typical of many decomposition reactions that are found to follow first-order kinetics, implying that the process is unimolecular. Until about 1921, chemists did not understand the role of collisions in unimolecular processes. It turns out that the mechanisms of such reactions are really rather complicated, and that at very low pressures they do follow second-order kinetics. Such reactions are more properly described as pseudounimolecular.
Activation energy
Higher temperatures, faster reactions
The chemical reactions associated with most food spoilage are catalyzed by enzymes produced by the bacteria which mediate these processes. It is common knowledge that chemical reactions occur more rapidly at higher temperatures. Everyone knows that milk turns sour much more rapidly if stored at room temperature rather than in a refrigerator, butter goes rancid more quickly in the summer than in the winter, and eggs hard-boil more quickly at sea level than in the mountains. For the same reason, cold-blooded animals such as reptiles and insects tend to be noticeably more lethargic on cold days.
It is not hard to understand why this should be. Thermal energy relates direction to motion at the molecular level. As the temperature rises, molecules move faster and collide more vigorously, greatly increasing the likelyhood of bond cleavages and rearrangements as described above.
Activation energy diagrams
Most reactions involving neutral molecules cannot take place at all until they have acquired the energy needed to stretch, bend, or otherwise distort one or more bonds. This critical energy is known as the activation energy of the reaction. Activation energy diagrams of the kind shown below plot the total energy input to a reaction system as it proceeds from reactants to products.
In examining such diagrams, take special note of the following:
- The "reaction coordinate" plotted along the abscissa represents the changes in atomic coordinates as the system progresses from reactants to products. In the very simplest elementary reactions it might correspond to the stretching or twisting of a particular bond, and be shown to a scale. In general, however, the reaction coordinate is a rather abstract concept that cannot be tied to any single measurable and scaleable quantity.
- The activated complex (also known as the transition state) represents the structure of the system as it exists at the peak of the activation energy curve. It does not correpond to an identifiable intermediate structure (which would more properly be considered the product of a separate elementary process), but rather to whatever configuration of atoms exists during the collision, which lasts for only about 0.1 picosecond.
- Activation energy diagrams always incorporate the energetics (ΔU or ΔH) of the net reaction, but it is important to understand that the latter quantities depend solely on the thermodynamics of the process which are always independent of the reaction pathway. This means that the same reaction can exhibit different activation energies if it can follow alternative pathways.
- With a few exceptions for very simple processes, activation energy diagrams are largely conceptual constructs based on our standard collision model for chemical reactions. It would be unwise to read too much into them.
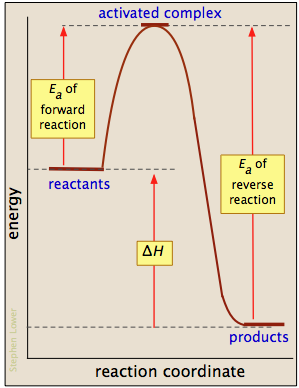
Gallery of activation energy plots
Activation energy diagrams can describe both exothermic and endothermic reactions:
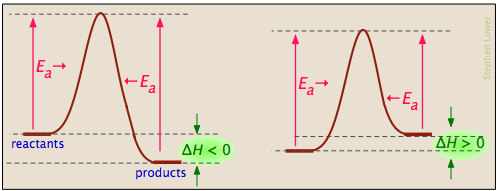
... and the activation energies of the forward reaction can be large, small, or zero (independently, of course, of the value of ΔH):
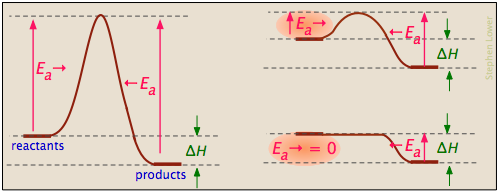
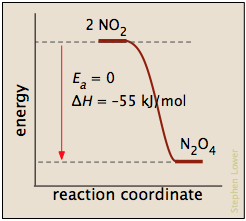
Processes with zero activation energy most commonly involve the combination of oppositely-charged ions or the pairing up of electrons in free radicals, as in the dimerization of nitric oxide (which is an odd-electron molecule).
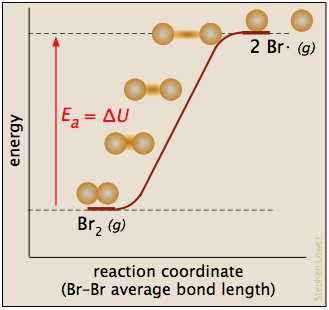
In this plot for the dissociation of bromine, the Ea is just the enthalpy of atomization
Br2(g) → 2 Br· (g)
and the reaction coordinate corresponds roughly to the stretching of the vibrationally-excited bond. The "activated complex", if it is considered to exist, is just the last, longest "stretch". The reverse reaction, being the recombination of two radicals, occurs immediately on contact.
Where does the activation energy come from?
In most cases, the activation energy is supplied by thermal energy, either through intermolecular collisions or (in the case of thermal dissocation) by thermal excitation of a bond-stretching vibration to a sufficiently high quantum level.
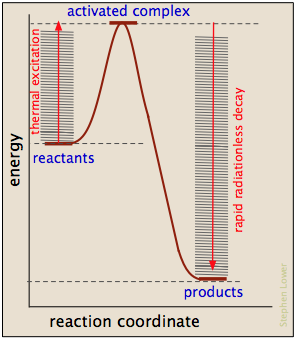
As products are formed, the activation energy is returned in the form of vibrational energy which is quickly degraded to heat. It's worth noting, however, that other sources of activation energy are sometimes applicable:
- Absorption of light by a molecule (photoexcitation) can be a very clean and efficient, but it doesn't always work. It's not enough that the wavelength of the light correspond to the activation energy; it must also fall within the absorption spectrum of the molecule, and (in a complex molecule) enough of it must end up in the right part of the molecule, such as in a particular bond.
- Electrochemical activation. Molecules capable of losing or gaining electrons at the surface of an electrode can undergo activation from an extra potential (known as the overvoltage) between the electrode and the solution. The electrode surface often plays an active role, so the process is also known as electrocatalysis.
Catalysts can reduce activation energy
A catalyst is usually defined as a substance that speeds up a reaction without being consumed by it. More specifically, a catalyst provides an alternative, lower activation energy pathway between reactants and products. As such, they are vitally important to chemical technology; approximately 95% of industrial chemical processes involve catalysts of various kind. In addition, most biochemical processes that occur in living organisms are mediated by enzymes, which are catalysts made of proteins.
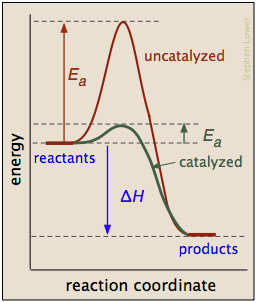
It is important to understand that a catalyst affects only the kinetics of a reaction; it does not alter the thermodynamic tendency for the reaction to occur. Thus there is a single value of ΔH for the two pathways depicted in the plot on the right
Temperature and kinetic energy
A review of the principles of gas molecular velocities and the Boltzmann distribution can be found on the "KMT-classic" page.
In the vast majority of cases, we depend on thermal actvation, so the major factor we need to consider is what fraction of the molecules possess enough kinetic energy to react at a given temperature. According to kinetic molecular theory, a opulation of molecules at a given temperature is distributed over a variety of kinetic energies that is described by the Maxwell-Boltzman distribution law.
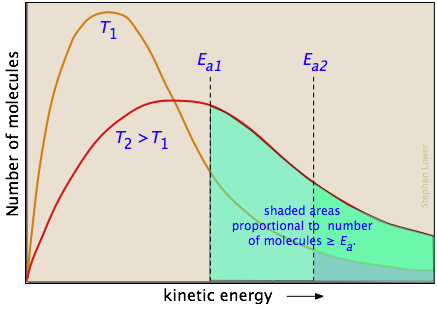
The two distribution plots shown here are for a lower temperature T1 and a higher temperature T2. The area under each curve represents the total number of molecules whose energies fall within particular range. The shaded regions indicate the number of molecules which are sufficiently energetic to meet the requirements dictated by the two values of Ea that are shown.
It is clear from these plots that the fraction of molecules whose kinetic energy exceeds the activation energy increases quite rapidly as the temperature is raised. This the reason that virtually all chemical reactions (and all elementary reactions) are more rapid at higher temperatures.
2 The Arrhenius law
By 1890 it was common knowledge that higher temperatures speed up reactions, often doubling the rate for a 10-degree rise, but the reasons for this were not clear. Finally, in 1899, the Swedish chemist Svante Arrhenius (1859-1927) combined the concepts of activation energy and the Boltzmann disribution law into one of the most important relationships in physical chemistry:

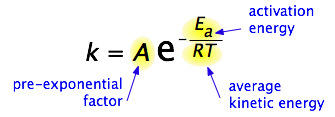
Take a moment to focus on the meaning of this equation, neglecting the A factor for the time being.
First, note that this is another form of the exponential decay law we discussed in the previous section of this series. What is "decaying" here is not the concentration of a reactant as a function of time, but the magnitude of the rate constant as a function of the exponent –Ea /RT. And what is the significance of this quantity? If you recall that RT is the average kinetic energy, it will be apparent that the exponent is just the ratio of the activation energy Ea to the average kinetic energy. The larger this ratio, the smaller the rate (hence the negative sign.) This means that high temperature and low activation energy favor larger rate constants, and thus speed up the reaction. And because these terms occur in an exponent, their effects on the rate are quite substantial.
The two plots below show the effects of the activation energy (denoted here by E‡) on the rate constant. Even a modest activation energy of 50 kJ/mol reduces the rate by a factor of 108.
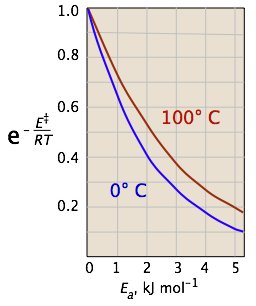
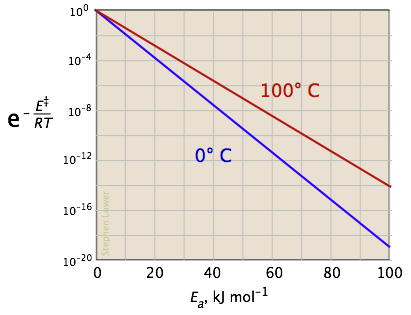
The logarithmic scale in the right-hand plot leads to nice straight lines, as described under the next heading below.
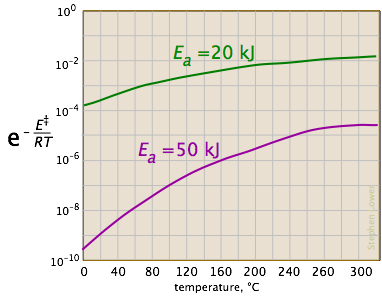
Looking at the role of temperature, we see a similar effect. (If the x-axis were in "kilodegrees" the slopes would be more comparable in magnitude with those of the kilojoule plot at the above right.)
Determining the activation energy
The Arrhenius equation
\[k=A \mathrm{e}^{-E_{a} / R T}\]
can be written in a non-exponential form which is often more convenient to use and to interpret graphically. Taking the logarithms of both sides and separating the exponential and pre-exponential terms yields
\[\ln k=\ln \left(A \mathrm{e}^{-E_{\mathrm{a}} / R T}\right)=\ln A+\ln \left(\mathrm{e}^{-E_{\mathrm{a}} / R T}\right)\]
\[\ln k=\ln A-\dfrac{E_{a}}{R T}\]
which is the equation of a straight line whose slope is \(–E_a /R\). This affords a simple way of determining the activation energy from values of \(k\) observed at different temperatures; we just plot \(\ln k\) as a function of \(1/T\).
Thus for the isomerization of cyclopropane to propene

the following data were obtained (calculated values shaded in pink):
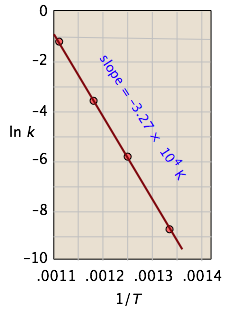
| T, °C | 477 | 523 | 577 | 623 |
|---|---|---|---|---|
| 1/T, K–1 × 103 | 1.33 | 1.25 | 1.18 | 1.11 |
| k, s–1 | 0.00018 | 0.0027 | 0.030 | 0.26 |
| ln k | –8.62 | –5.92 | –3.51 | –1.35 |
From the calculated slope, we have
– (Ea/R) = –3.27 × 104 K
Ea=– (8.314 J mol–1 K–1) (–3.27 × 104 K) = 273 kJ mol–1
Comment: This activation energy is rather high, which is not surprising because a carbon-carbon bond must be broken in order to open the cyclopropane ring. (C–C bond energies are typically around 350 kJ/mol.) This is why the reaction must be carried out at high temperature.
You don't always need a plot
(... if you are willing to live a bit dangerously!) Since the ln k-vs.-1/T plot yields a straight line, it is often convenient to estimate the activation energy from experiments at only two temperatures. To see how this is done, consider that
\[\ln k_{2}-\ln k_{1}=\left(\ln A-\frac{E_{a}}{R T_{2}}\right)-\left(\ln A-\frac{E_{a}}{R T_{1}}\right)=\frac{E_{a}}{R}\left(\frac{1}{T_{1}}-\frac{1}{T_{2}}\right) \nonumber\]
(... in which we have made the ln-A term disappear by subtracting the expressions for the two ln-k terms.) Solving the expression on the right for the activation energy yields
\[E_{a}=\dfrac{R \ln \dfrac{k_{2}}{k_{1}}}{\dfrac{1}{T_{1}}-\dfrac{1}{T_{2}}} \nonumber\]
A widely used rule-of-thumb for the temperature dependence of a reaction rate is that a ten-C° rise in the temperature approximately doubles the rate. (This is obviously not generally true, especially when a strong covalent bond must be broken.) But for a reaction that does show this behavior, what would the activation energy be?
Solution
We will center our ten-degree interval at 300 K. Substituting into the above expression yields
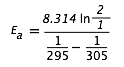 = (8.314)(0.693) / (.00339 - 0.00328)
= (8.314)(0.693) / (.00339 - 0.00328)
= (5.76 J mol–1 K–1) / (0.00011 K–1) = 52400 J mol–1 = 52.4 kJ mol–1
It takes about 3.0 minutes to cook a hard-boiled egg in Los Angeles, but at the higher altitude of Denver, where water boils at 92°C, the cooking time is 4.5 minutes. Use this information to estimate the activation energy for the coagulation of egg albumin protein.
Solution:
The ratio of the rate constants at the elevations of LA and Denver is 4.5/3.0 = 1.5, and the respective temperatures are 373K and 365K. With the subscripts 2 and 1 referring to LA and Denver respectively, we have
Ea = (8.314)(ln 1.5) / (1/365 – 1/273) = (8.314)(.405) / (0.00274 – 0.00366)
= (3.37 J mol–1 K–1) / (0.000923 K–1) = 3650 J mol–1 = 3.65 kJ mol–1
Comment: This rather low value seems reasonable because protein denaturation involves the disruption of relatively weak hydrogen bonds; no covalent bonds are broken
Crickets and popcorn
- Many biological processes exhibit a temperature dependence that follows the Arrhenius law, and can thus be characterized by an activation energy. See this interesting Dartmouth U. page that looks at the kinetics of cricket chirps.
The pre-exponential factor
It is now time to focus in on the pre-exponential term A in the Arrhenius equation. We have been neglecting it because it is not directly involved in relating temperature and activation energy, which is the main practical use of the equation. But since A multiplies the exponential term, its value clearly contributes to the value of the rate constant and thus of the rate.
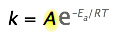
and of the temperature.
If this fraction were unity, the Arrhenius law would reduce to
\[k = A\]
In other words, A is the fraction of molecules that would react if either the activation energy were zero, or if the kinetic energy of all molecules exceeded Ea — admittedly, an uncommon scenario.
It's all about collisions
So what would limit the rate constant if there were no activation energy requirements? The most obvious factor would be the rate at which reactant molecules come into contact. This can be calculated from kinetic molecular theory and is known as the frequency- or collision factor Z. In some reactions, the relative orientation of the molecules at the point of collision is important, so we can also define a geometrical or steric factor (commonly denoted by ρ (Greek lower case rho).
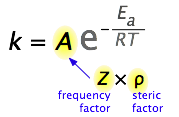
In general, we can express A as the product of these two factors:
\[A = Zρ\]
Values of \(ρ\) are generally very difficult to assess; they are sometime estimated by comparing the observed rate constant with the one in which A is assumed to be the same as Z.
Direction makes a difference
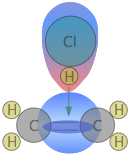
The more complicated the structures of the reactants, the more likely that the value of the rate constant will depend on the trajectories at which the reactants approach each other. We showed one example of this near the top of the page, but for another, consider the addition of a hydrogen halide such as HCl to the double bond of an alkene, converting it to a chloroalkane. This kind of electrophilic addition reaction is well-known to all students of organic chemistry.
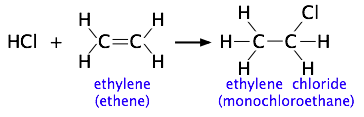
Experiments have shown that the reaction only takes place when the HCl molecule approaches the alkene with its hydrogen-end, and in a direction that is approximately perpendicular to the double bond, as shown at  below.
below.
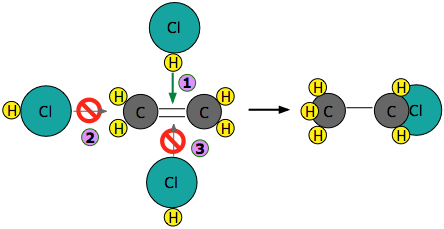
The reason for this becomes apparent when we recall that HCl is highly polar owing to the high electronegativity of chlorine, so that the hydrogen end of the molecule is slightly positive. The double bond of ethene consists of two clouds of negative charge corresponding to the σ (sigma) and π (pi) molecular orbitals. The latter, which extends above and below the plane of the C2H4 molecule, interacts with and attracts the HCl molecule.
If, instead, the HCl approaches with its chlorine end leading as in  , electrostatic repulsion between the like charges causes the two molecules to bounce away from each other before any reaction can take place. The same thing happens in
, electrostatic repulsion between the like charges causes the two molecules to bounce away from each other before any reaction can take place. The same thing happens in  ; the electronegativity difference between carbon and hydrogen is too small to make the C–H bond sufficiently polar to attract the incoming chlorine atom.
; the electronegativity difference between carbon and hydrogen is too small to make the C–H bond sufficiently polar to attract the incoming chlorine atom.
The lesson you should take from this example is that once you start combining a variety of chemical principles, you gradually develop what might be called "chemical intuition" which you can apply to a wide variety of problems. This is far more important than memorizing specific examples. Now that you know what it takes to get a reaction started, you are ready for the next lesson that describes their actual mechanisms.


