8.7: Colligative Properties and Entropy

All four solution effects (Reduced Vapor Pressure, Freezing Point depression, Boiling Point Elevation, Osmotic pressure) result from “dilution” of the solvent by the added solute. Because of this commonality they are referred to as colligative properties (Lat. co ligare, connected to.) The key role of the solvent concentration is obscured by the greatly-simplified expressions used to calculate the magnitude of these effects, in which only the solute concentration appears. The details of how to carry out these calculations and the many important applications of colligative properties are covered elsewhere. Our purpose here is to offer a more complete explanation of why these phenomena occur.

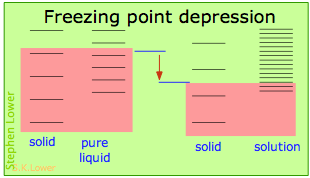
Basically, these all result from the effect of dilution of the solvent on its entropy, and thus in the increase in the density of energy states of the system in the solution compared to that in the pure liquid. Equilibrium between two phases (liquid-gas for boiling and solid-liquid for freezing) occurs when the energy states in each phase can be populated at equal densities. The temperatures at which this occurs are depicted by the shading.

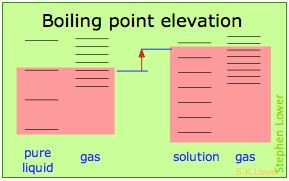
• Dilution of the solvent adds new energy states to the liquid, but does not affect the vapor phase. This raises the temperature required to make equal numbers of microstates accessible in the two phases.
• Dilution of the solvent adds new energy states to the liquid, but does not affect the solid phase. This reduces the temperature required to make equal numbers of states accessible in the two phases.

Effects of pressure on the entropy: Osmotic Pressure

When a liquid is subjected to hydrostatic pressure— for example, by an inert, non-dissolving gas that occupies the vapor space above the surface, the vapor pressure of the liquid is raised. The pressure acts to compress the liquid very slightly, effectively narrowing the potential energy well in which the individual molecules reside and thus increasing their tendency to escape from the liquid phase. (Because liquids are not very compressible, the effect is quite small; a 100-atm applied pressure will raise the vapor pressure of water at 25°C by only about 2 torr.) In terms of the entropy, we can say that the applied pressure reduces the dimensions of the "box" within which the principal translational motions of the molecules are confined within the liquid, thus reducing the density of energy states in the liquid phase.

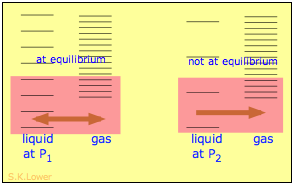
Applying hydrostatic pressure to a liquid increases the spacing of its microstates, so that the number of energetically accessible states in the gas, although unchanged, is relatively greater— thus increasing the tendency of molecules to escape into the vapor phase. In terms of free energy, the higher pressure raises the free energy of the liquid, but does not affect that of the gas phase.

This phenomenon can explain osmotic pressure. Osmotic pressure, students must be reminded, is not what drives osmosis, but is rather the hydrostatic pressure that must be applied to the more concentrated solution (more dilute solvent) in order to stop osmotic flow of solvent into the solution. The effect of this pressure \(\Pi\) is to slightly increase the spacing of solvent energy states on the high-pressure (dilute-solvent) side of the membrane to match that of the pure solvent, restoring osmotic equilibrium.

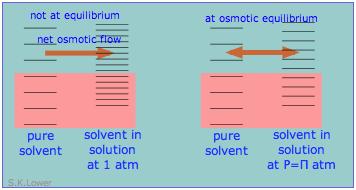
Osmotic pressure does not drive osmosis, but is rather the hydrostatic pressure that must be applied to the more concentrated solution (more dilute solvent) in order to stop osmotic flow of solvent into the solution.