3.1: Units and Dimensions
- Page ID
- 78928
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Make sure you thoroughly understand the following essential ideas which have been presented above. It is especially important that you know the precise meanings of all the italicized terms in the context of this topic.
- Describe the names and abbreviations of the SI base units and the SI decimal prefixes.
- Define the liter and the metric ton in these units.
- Explain the meaning and use of unit dimensions; state the dimensions of volume.
- State the quantities that are needed to define a temperature scale, and show how these apply to the Celsius, Kelvin, and Fahrenheit temperature scales.
- Explain how a Torricellian barometer works.
Have you ever estimated a distance by “stepping it off”— that is, by counting the number of steps required to take you a certain distance? Or perhaps you have used the width of your hand, or the distance from your elbow to a fingertip to compare two dimensions. If so, you have engaged in what is probably the first kind of measurement ever undertaken by primitive mankind. The results of a measurement are always expressed on some kind of a scale that is defined in terms of a particular kind of unit. The first scales of distance were likely related to the human body, either directly (the length of a limb) or indirectly (the distance a man could walk in a day).
As civilization developed, a wide variety of measuring scales came into existence, many for the same quantity (such as length), but adapted to particular activities or trades. Eventually, it became apparent that in order for trade and commerce to be possible, these scales had to be defined in terms of standards that would allow measures to be verified, and, when expressed in different units (bushels and pecks, for example), to be correlated or converted.
Over the centuries, hundreds of measurement units and scales have developed in the many civilizations that achieved some literate means of recording them. Some, such as those used by the Aztecs, fell out of use and were largely forgotten as these civilizations died out. Other units, such as the various systems of measurement that developed in England, achieved prominence through extension of the Empire and widespread trade; many of these were confined to specific trades or industries. The examples shown here are only some of those that have been used to measure length or distance. The history of measuring units provides a fascinating reflection on the history of industrial development.
The most influential event in the history of measurement was undoubtedly the French Revolution and the Age of Rationality that followed. This led directly to the metric system that attempted to do away with the confusing multiplicity of measurement scales by reducing them to a few fundamental ones that could be combined in order to express any kind of quantity. The metric system spread rapidly over much of the world, and eventually even to England and the rest of the U.K. when that country established closer economic ties with Europe in the latter part of the 20th Century. The United States is presently the only major country in which “metrication” has made little progress within its own society, probably because of its relative geographical isolation and its vibrant internal economy.
Science, being a truly international endeavor, adopted metric measurement very early on; engineering and related technologies have been slower to make this change, but are gradually doing so. Even the within the metric system, however, a variety of units were employed to measure the same fundamental quantity; for example, energy could be expressed within the metric system in units of ergs, electron-volts, joules, and two kinds of calories. This led, in the mid-1960s, to the adoption of a more basic set of units, the Systeme Internationale (SI) units that are now recognized as the standard for science and, increasingly, for technology of all kinds.
The SI base Units
In principle, any physical quantity can be expressed in terms of only seven base units. Each base unit is defined by a standard which is described in the NIST Web site.
| length | meter | m |
| mass | kilogram | kg |
| time | second | s |
| temperature (absolute) | kelvin | K |
| amount of substance | mole | mol |
| electric current | ampere | A |
| luminous intensity | candela | cd |
A few special points about some of these units are worth noting:
- The base unit of mass is unique in that a decimal prefix (see below) is built-in to it; that is, it is not the gram, as you might expect.
- The base unit of time is the only one that is not metric. Numerous attempts to make it so have never garnered any success; we are still stuck with the 24:60:60 system that we inherited from ancient times. (The ancient Egyptians of around 1500 BC invented the 12-hour day, and the 60:60 part is a remnant of the base-60 system that the Sumerians used for their astronomical calculations around 100 BCE.)
- Of special interest to Chemistry is the mole, the base unit for expressing the quantity of matter. Although the number is not explicitly mentioned in the official definition, chemists define the mole as Avogadro’s number (approximately \(6.02 \times 10^{23}\)) of anything.
The SI decimal prefixes
Owing to the wide range of values that quantities can have, it has long been the practice to employ prefixes such as milli and mega to indicate decimal fractions and multiples of metric units. As part of the SI standard, this system has been extended and formalized.
| prefix | abbreviation | multiplier | prefix | abbreviation | multiplier |
|---|---|---|---|---|---|
| exa | E | 1018 | deci | d | 10–1 |
| peta | P | 1015 | centi | c | 10–2 |
| tera | T | 1012 | milli | m | 10–3 |
| giga | G | 109 | micro | μ | 10–6 |
| mega | M | 106 | nano | n | 10–9 |
| kilo | k | 103 | pico | p | 10–12 |
| hecto | h | 102 | femto | f | 10–15 |
| deca | da | 10 | atto | a | 10–18 |
For a more complete table, see the NIST page on SI prefixes
Non-SI Units
There is a category of units that are “honorary” members of the SI in the sense that it is acceptable to use them along with the base units defined above. These include such mundane units as the hour, minute, and degree (of angle), etc., but the three shown here are of particular interest to chemistry, and you will need to know them.
- liter (\(L\)) \[1\, L = 1\, dm^3 = 10^{–3} m^3 \nonumber\]
- metric ton (\(t\)) \[1\, t = 10^3 kg \nonumber\]
- atomic mass unit (\(u\)) \[1\, u = 1.66054×10^{–27}\, kg \nonumber\]
Most of the physical quantities we actually deal with in science and also in our daily lives, have units of their own: volume, pressure, energy and electrical resistance are only a few of hundreds of possible examples. It is important to understand, however, that all of these can be expressed in terms of the SI base units; they are consequently known as derived units.
In fact, most physical quantities can be expressed in terms of one or more of the following five fundamental units:
| mass M | length L | time T | electric charge Q | temperature Θ (theta) |
Consider, for example, the unit of volume, which we denote as V. To measure the volume of a rectangular box, we need to multiply the lengths as measured along the three coordinates:
\[V = x · y · z\]
We say, therefore, that volume has the dimensions of length-cubed:
\[dim.V = L^3\]
Thus the units of volume will be m3 (in the SI) or cm3, ft3 (English), etc. Moreover, any formula that calculates a volume must contain within it the L3 dimension; thus the volume of a sphere is 4/3 πr3.
Consider, for example, the unit of volume, which we denote as V. To measure the volume of a rectangular box, we need to multiply the lengths as measured along the three coordinates: V = x · y · z We say, therefore, that volume has the dimensions of length-cubed: dim.V = L3 Thus the units of volume will be m3 (in the SI) or cm3, ft3 (English), etc. Moreover, any formula that calculates a volume must contain within it the L3 dimension; thus the volume of a sphere is 4/3 πr3.
Find the dimensions of energy.
Solution
When mechanical work is performed on a body, its energy increases by the amount of work done, so the two quantities are equivalent and we can concentrate on work. The latter is the product of the force applied to the object and the distance it is displaced. From Newton’s law, force is the product of mass and acceleration, and the latter is the rate of change of velocity, typically expressed in meters per second per second. Combining these quantities and their dimensions yields the result shown here.
Units and Their Ranges in Chemistry
In this section, we will look at some of the quantities that are widely encountered in Chemistry, and at the units in which they are commonly expressed. In doing so, we will also consider the actual range of values these quantities can assume, both in nature in general, and also within the subset of nature that chemistry normally addresses. In looking over the various units of measure, it is interesting to note that their unit values are set close to those encountered in everyday human experience
Mass and Weight
These two quantities are widely confused. Although they are often used synonymously in informal speech and writing, they have different dimensions: weight is the force exerted on a mass by the local gravational field:
\[f = m a = m g\]
where g is the acceleration of gravity. While the nominal value of the latter quantity is 9.80 m s–2 at the Earth’s surface, its exact value varies locally. Because it is a force, the SI unit of weight is properly the newton, but it is common practice (except in physics classes!) to use the terms "weight" and "mass" interchangeably, so the units kilograms and grams are acceptable in almost all ordinary laboratory contexts.
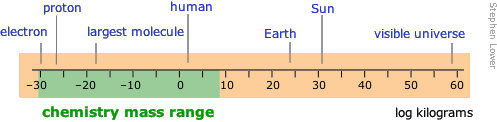
The range of masses spans 90 orders of magnitude, more than any other unit. The range that chemistry ordinarily deals with has greatly expanded since the days when a microgram was an almost inconceivably small amount of material to handle in the laboratory; this lower limit has now fallen to the atomic level with the development of tools for directly manipulating these particles. The upper level reflects the largest masses that are handled in industrial operations, but in the recently developed fields of geochemistry and environmental chemistry, the range can be extended indefinitely. Flows of elements between the various regions of the environment (atmosphere to oceans, for example) are often quoted in teragrams.
Length
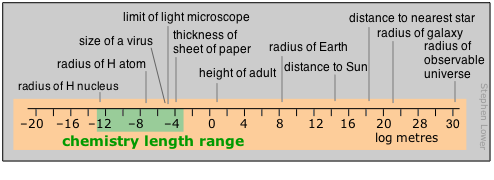
Chemists tend to work mostly in the moderately-small part of the distance range. Those who live in the lilliputian world of crystal- and molecular structures and atomic radii find the picometer a convenient currency, but one still sees the older non-SI unit called the Ångstrom used in this context; 1Å = 10–10 m = 100pm. Nanotechnology, the rage of the present era, also resides in this realm. The largest polymeric molecules and colloids define the top end of the particulate range; beyond that, in the normal world of doing things in the lab, the centimeter and occasionally the millimeter commonly rule.
Time
For humans, time moves by the heartbeat; beyond that, it is the motions of our planet that count out the hours, days, and years that eventually define our lifetimes. Beyond the few thousands of years of history behind us, those years-to-the-powers-of-tens that are the fare for such fields as evolutionary biology, geology, and cosmology, cease to convey any real meaning for us. Perhaps this is why so many people are not very inclined to accept their validity.
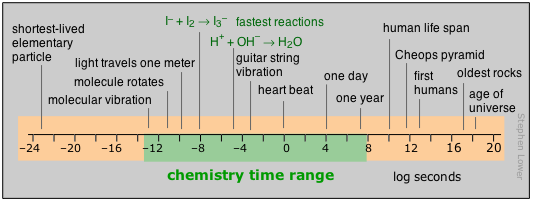
Most of what actually takes place in the chemist’s test tube operates on a far shorter time scale, although there is no limit to how slow a reaction can be; the upper limits of those we can directly study in the lab are in part determined by how long a graduate student can wait around before moving on to gainful employment. Looking at the microscopic world of atoms and molecules themselves, the time scale again shifts us into an unreal world where numbers tend to lose their meaning. You can gain some appreciation of the duration of a nanosecond by noting that this is about how long it takes a beam of light to travel between your two outstretched hands. In a sense, the material foundations of chemistry itself are defined by time: neither a new element nor a molecule can be recognized as such unless it lasts around sufficiently long enough to have its “picture” taken through measurement of its distinguishing properties.
Temperature
Temperature, the measure of thermal intensity, spans the narrowest range of any of the base units of the chemist’s measure. The reason for this is tied into temperature’s meaning as a measure of the intensity of thermal kinetic energy. Chemical change occurs when atoms are jostled into new arrangements, and the weakness of these motions brings most chemistry to a halt as absolute zero is approached. At the upper end of the scale, thermal motions become sufficiently vigorous to shake molecules into atoms, and eventually, as in stars, strip off the electrons, leaving an essentially reaction-less gaseous fluid, or plasma, of bare nuclei (ions) and electrons.
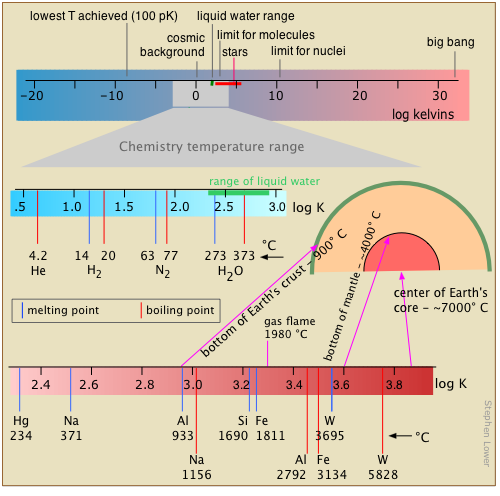
We all know that temperature is expressed in degrees. What we frequently forget is that the degree is really an increment of temperature, a fixed fraction of the distance between two defined reference points on a temperature scale.
Pressure
Pressure is the measure of the force exerted on a unit area of surface. Its SI units are therefore newtons per square meter, but we make such frequent use of pressure that a derived SI unit, the pascal, is commonly used:
1 Pa = 1 N m–2
The concept of pressure first developed in connection with studies relating to the atmosphere and vacuum that were first carried out in the 17th century. The molecules of a gas are in a state of constant thermal motion, moving in straight lines until experiencing a collision that exchanges momentum between pairs of molecules and sends them bouncing off in other directions. This leads to a completely random distribution of the molecular velocities both in speed and direction— or it would in the absence of the Earth’s gravitational field which exerts a tiny downward force on each molecule, giving motions in that direction a very slight advantage. In an ordinary container this effect is too small to be noticeable, but in a very tall column of air the effect adds up: the molecules in each vertical layer experience more downward-directed hits from those above it. The resulting force is quickly randomized, resulting in an increased pressure in that layer which is then propagated downward into the layers below.
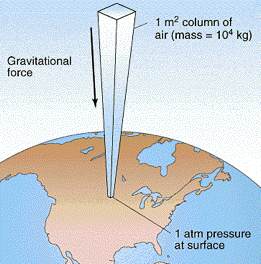
At sea level, the total mass of the sea of air pressing down on each 1-cm2 of surface is about 1034 g, or 10340 kg m–2. The force (weight) that the Earth’s gravitional acceleration g exerts on this mass is
f = ma = mg = (10340 kg m–2)(9.81 m s–2) = 1.013 × 105 kg m s–2 = 1.013 × 105 newtons
resulting in a pressure of
\[1.013 × 10^5 N\, m^{–2} = 1.013 × 10^5 pa.\]
The actual pressure at sea level varies with atmospheric conditions, so it is customary to define standard atmospheric pressure as 1 atm = 1.013105 pa or 101 kpa. Although the standard atmosphere is not an SI unit, it is still widely employed. In meteorology, the bar, exactly 1.000 × 105 = 0.967 atm, is often used.
In the early 17th century, the Italian physicist and mathematician Evangalisto Torricelli invented a device to measure atmospheric pressure. The Torricellian barometer consists of a vertical glass tube closed at the top and open at the bottom. It is filled with a liquid, traditionally mercury, and is then inverted, with its open end immersed in the container of the same liquid. The liquid level in the tube will fall under its own weight until the downward force is balanced by the vertical force transmitted hydrostatically to the column by the downward force of the atmosphere acting on the liquid surface in the open container. Torricelli was also the first to recognize that the space above the mercury constituted a vacuum, and is credited with being the first to create a vacuum.

One standard atmosphere will support a column of mercury that is 76 cm high, so the “millimeter of mercury”, now more commonly known as the torr, has long been a common pressure unit in the sciences: 1 atm = 760 torr.


