Carbon Oxides

Discussion Questions

• What are the molecular structures of carbon oxides?
• What atomic orbitals are involved in the molecular orbitals of carbon oxides?
• Why do CO molecules form strong bonds with metal atoms in carbonyls?
• What are some of the applications of carbon oxides?
• How has carbon dioxide level changed?
• What measure can be taken to reduce CO₂ emission?

Carbon Oxides

Carbon forms two important gases with oxygen: carbon monoxide, CO, and carbon dioxide, CO₂. Carbon oxides are important components of the atmosphere, and they are parts of the carbon cycle.

Carbon dioxide is naturally produced by respiration and metabolism, and consumed by plants in their photosynthesis. Since the industrial revolution, greater amount of carbon dioxide has been generated for over a hundred years due to increased industrial activities.

Today, information on carbon oxides is important. Issues related to carbon oxides have no boundaries. The Carbon Dioxide Information Analysis Center (CADIAC) provides global datasets on carbon dioxide and other atmosphere gases and climate. These datasets are available to international researchers, policymakers, managers, and educators to help evaluate complex environmental issues associated with potential climate change.

Carbon monoxide is also a national and global concern. The Consumer Product Safety Commission (CPSC) considers CO a senseless killer, and it provides information on CO poisoning and detection.

What are the molecular structures of carbon oxides?

The formation of carbon oxides is due to electronic configurations of carbon and oxygen. They have 4 and 6 valence electrons respectively. Using these valence electrons, we can give the Lewis dot structure for CO and three resonance structures for CO2 as follows:

           ..     ..     ..                ..
:C:::O:    :O::C::O: « :O:C:::O: « :O:::C:O:
                         ''                ''

These formulas suggest very strong bonding between carbon and oxygen in these gaseous molecules: triple bond in CºO, and double bonds in O=C=O. However, a formula containing a triple bond contribute to the resonance structure.

What atomic orbitals are involved in the molecular orbitals of carbon oxides?

The chemical bonding is more of an interpretation of the molecules in view of their properties. Using results from quantum mechanical approach, we may start by reviewing the electronic configurations of carbon and oxygen:

C: 1s² 2s²2p²
O: 1s² 2s²2p⁴

Thus, the carbon has 4 valence electrons and oxygen has 6 valence electrons. The s and p atomic orbitals are available for chemical bonding.

The valence bond approach suggests that p orbitals of carbon and oxygen are used in these molecules. In CO, only one such atomic orbital from each atom of C and O are employed to form a sigma, s, bond, and overlapping of two p orbitals leads to the formation of the two pi, p, bond. Thus, the bond order is 3 between C and O in CºO.

Note

A \(CO\) molecule has the same number of electrons as \(N_2\), and these molecules are said to be iso-electronic. The N₂ molecule is also represented by NºN.

The molecular orbital (MO) approach for CO is describe in the lecture, and the MO energy level diagram has been given there. The plots of contours of equal electron densities has also been shown in earlier lectures, and the diagram for CO molecular orbitals is shown below:

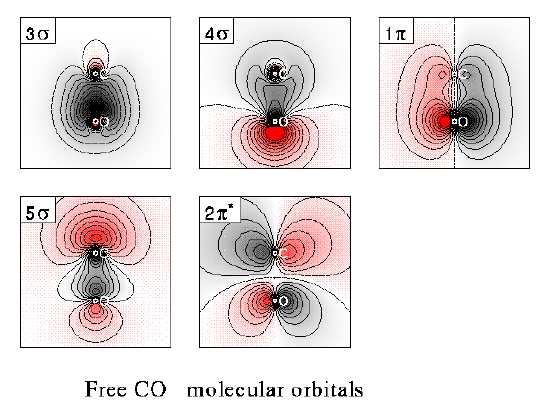
The valence bond approach for CO₂ bonding is also very interesting. The two sp hybrid orbitals of central carbon overlaps with one p orbital from each of the oxygen atoms to from the two C-O s bonds in O-C-O. The two remaining p orbitals of carbon overlap with a p orbital each of the two oxygen atoms forming two p bonds, leading to the formation of O=C=O.

Here is a challenge: find a suitable diagram for either valence bond approach or for the MO approach for carbon dioxide in the web.

Why do CO molecules form strong bonds with metal atoms in carbonyls?

Molecules of \(CO\) and \(NN\) have two \(\pi\) bonds. Since the two atoms in \(CO\) are different, this made \(CO\) much more reactive than nitrogen. Indeed, \(CO\) forms many carbonyls with metal atoms or ions. For example, you have encountered some of the following carbonyls on the page of Heterogeneous catalysts

• Ni(CO)4
• Fe(CO)5
• Co2(u-CO)2(CO)6, (u-CO meaning CO bridged between two metal atoms)
• Mn2(CO)10
• Fe3(CO)12
• Co4(CO)12
• Rh4(CO)12
• CFe5(CO)15
• Rh6(CO)16
• Os6(CO)18

The study of metal carbonyls started with the discover of ferrocene Fe(C₅H₅)₂ and now hundreds if not thousands of metal carbonyls have been synthesized..

A sbond is formed between the carbon of CO and the metal atom. Such a bonding is very sensible if we consider the sp hybrid atomic orbitals of carbon being used in this case. Since there are two electrons in this orbitals of CO, the metal atom gains at least some fraction of electron due to the formation of this bond.

The empty antibonding \(pi\) orbital \(\pi^*\) of \(CO\) has the right symmetry and orientation to receive the back-donated electron from the filled d-orbitals of the metal atom. The back donation reinforce the sigma bond, and vice versa. This type of bonding has been called the synergic bonding mechanism by Cotton and Wilkinson in their Advanced Inorganic Chemistry. A diagram showing this type of bonding scheme is shown on page 159 in Inorganic Chemistry by Swaddle.

What are some of the applications of carbon oxides?

Carbon oxides are useful commodities. A gas containing CO and hydrogen is called synthetic gas, because it can be converted to methanol using a catalyst. During the past few decades, many metal carbonyls have been prepared. These carbonyls are potential catalysts. When the metal carbonyl is a gas, the purified metal carbonyl gas can be used for the production of extra-pure metals.

Carbon dioxide is also a useful industrial gas. It is widely used in food and beverage industry. Here are some of its applications.

• making efferescent drinks
• manufacture of urea, CO(NH₂)₂, as fertilizer
• promote plant growth in green house
• making dry ice
• fire extinguisher
• provide an inert atmosphere for fruit and vegetable preservation
• as a supercritical fluid for solvent extraction

The critical temperature of carbon dioxide is only 304 K at a critical pressure of 7.39 MPa (almost 7 atm). These conditions can easily be met to generate supercritical carbon dioxide, which is a powerful and descriminating solvent. The supercritical fluid penetrates porous solids, evaporates without leaving a trace. Thus, this fluid is widely used as an extracting solvent. This fluid is also very useful in the field of analytical chemsitry.

On the high technology side, carbon dioxide lasers can provide a continuous laser beam from several milliwatts to several killowatts with a typical efficiency of 30%, one of the most efficient laser generation devices. This link also illustrates the basic theory of laser. Among many applications of laser, carbon dioxide laser has been used for skin resurfacing as an art of cosmetic surgery.

On the other hand, the heavier carbon dioxide usually stay in lower grounds, and when its concentration is very high, it can be a thread to living beings who will die of asphyxiation.

How has carbon dioxide level changed?

When Henry Ford put people to work on the assembly line, he did not worry about the consequence of automobile exhaust. He probably did not foresee the change of the society. Now everyone wants a piece of the carbondioxide generating machine. You can imagine that when all countries use as much energy as Canadians do, the carbon dioxide level of the atmosphere will be much higher. We need good measurements about carbon dioxide level in order to know how it is changing.

The National Oceanic and Atmospheric Administration (NOAA) of the U.S. is keeping track of it, and the measurements at Barrow, Alaska. The annual increase has been reported to be 1.49 ppm by volume per year. On the other hand, the atmospheric CO₂ concentration was about 280 ppm by volume in the 1700s before the industrial revolution, and it was 360 ppm in 1994. If you want more details about Carbon Dioxide Emissions in the U.S., this link is full of data.

Engineers, scientists, politician and the general public believe that increase level of CO₂ will cause the world to warm up, because some scientists have demonstrated their findings and the experts agreed. Lengthy discussion is required to present scientific evidences for the so called green house effect of CO₂, and hopefully some day you will be able to judge the argument yourself. I have not found simple and convincing evidence to present at this time. However, experts have suggested a correlation with the increase level of CO₂ and the average temperature of the globe.

What measure can be taken to reduce CO₂ emission?

The green house effect of \(CO_2\) has attracted attention not only of expert and politicians, the public pressure (mostly the news media) have made the reduction of \(CO_2\) emission an international priority. The United Nations Panel on Climate Change made several recommendations regarding \(CO_2\).

• use natural gas as fuel rather than coal or oil
• use solar or nuclear energy instead of fossil fuels for electricity generation
• reduce rate of deforestation
• limit use of automobiles

Well, what can be done at a personal level, as a community, and as a country requires the determination of individuals. This is a challenge for us all especially engineers, because they are at the forefront of many industries. We face many front for a solution to the problem of carbon dioxide emission.

Example 1

The standard enthalpy of formation of NO is 90.25 kJ / mol and the standard entropies of \(N_2\), \(O_2\), \(NO\) are 191.61, 205.138 and 210.761 J (K mol)^-1 respectively. Calculate the Gibb's energy for the reaction

\[\ce{N_2 + O_2 \rightarrow 2 NO}\nonumber \]

at standard conditions.

Solution

The entropy of formation for the above reaction is

\[\begin{align*} \Delta S^o &= 2 \times 210.761 - (205.138 + 191.61) \\[4pt] &= 24.77 \frac{J}{K mol} \end{align*}\]

The Gibb's energy of formation is then:

\[ \begin{align*} \Delta G^o &= \Delta H^o - T\Delta S^o \\[4pt] &= 180.5 - 298*0.02477 \\[4pt] & = 180.5 - 7.38 \,kJ \\[4pt] &= 173.12\, kJ \end{align*}\]

This value shows that the reaction is endothermic.

DISCUSSION

What is the equilibrium constant for the reaction as written and what is the implication of the result in the discussion of NO in air?

Contributors and Attributions

• Chung (Peter) Chieh (Professor Emeritus, Chemistry @ University of Waterloo)