Carbon Cycle

Discussion Questions

• How is carbon cycled at a global scale?

The Global Carbon Cycle

A scientist and an engineer may be called upon to solve a particular problem involving coal (carbon), gasoline (hydrocarbon), combustion of carbon or carbon containing fuel, lime stone, sea shells, carbon monoxide, or carbon dioxide. When we formulate a solution, we should be aware of the impact not only of the problem, but also of the solution for such a problem. Otherwise, the solution may result in a problem that is more expensive to solve later. Thus, it is important to know how carbon evolve at a global scale. The carbon cycle? is part of the Earth cycle. The diagram from this link is shown here, because it illustrate the global cycle of carbon without including respiration and metabolism. It illustrates the geological processes.

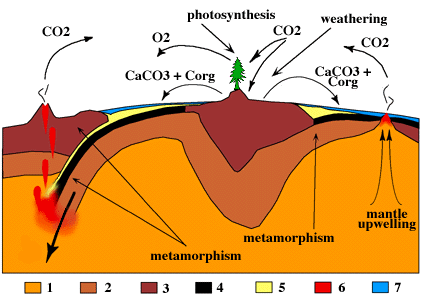
How is carbon cycled at a global scale?

The carbon atoms undergo a complicated chemistry forming what is known as the global carbon cycle, as do oxygen, nitrogen, and other elements; but the carbon cycle is the most widely recognized. An animal produces carbon dioxide and consumes oxygen in its metabolism of food. Glucose is a typical food and a metabolic reaction can be represented by:

\[C_6H_{12}O_6 + 6 O_2 \rightarrow 6 CO_2+ 6 H_2O\]

A plant and green bacteria, on the other hand, produces oxygen and consumes carbon dioxide in its photo synthesis. Energy in the form of electromagnetic radiation (or photons) is supplied so that the low-energy-content carbon dioxide can be converted to high-energy-content glucose. An overall reaction for the complicated multi-step photosynthesis reaction can be represented by:

\[6 CO_2+ 12 H_2O -- h\nu \rightarrow C_6H_{12}O_6 + 6 O_2 + 6 H_2O\]

At a glance, animals and plants make food for each other. The plants convert solar energy into high-energy food for the animals. Water is a reactant and a product in the photosynthesis. Radioactive labeled studies showed that the oxygen in the water produced comes from those in carbon dioxide. You may be thinking about plants with leaves that give beautiful flowers. In fact, primitive plants in the ocean play a more important role in in the photosynthesis process, because of the large number of them.

The solubility of carbon dioxide depends on its partial pressure. As we know, carbon dioxide dissolves in water to form carbonic acid:

\[CO_2+ H_2O \rightarrow H_2CO_3\]

\[H_2CO_3 \rightarrow H^+ + HCO_3^- K_{a1} = 4.2 \times 10^{-7}\]

\[HCO_3^- \rightarrow H^+ + CO_3^{2-} K_{a2} = 4.8 \times 10^{-11}\]

The dissolved carbon dioxide further reacts with metal ions in the water forming calcium and magnesium carbonates. The K_sp values for CaCO₃ and MgCO₃ are \(5\times 10^{-9}\) and \(3\times 10^{-3}\) respectively. Extensive limestone (CaCO₃) and dolomite (mixture of CaCO₃ and MgCO₃) have been formed this way.

\[CaCO_3 \rightarrow Ca^{2+} + CO_3^{2-} \;\;\ K_{sp} = 5 \times 10^{-9}\]

\[MgCO_3 \rightarrow Mg^{2+} + CO_3^{2-} \;\;\; K_{sp} = 3 \times 10^{-3}\]

Some believed that this is how lime stone produced. Lime stone is soluble in acidic solutions, which may be formed by dissolving large amount of carbon dioxide.

\[CaCO_{3(s)} + 2 H^+_{(aq)} \rightarrow Ca^{2+}{(aq)} + H_2CO_{3(aq)}\]

or,

\[CO2(aq) + H2O(l) + CaCO3(s) \rightarrow Ca2+(aq) + 2 HCO3-(aq)\]

When the concentration of carbon dioxide is reduced, the acidity decreases and the reverse reaction takes place forming a solid, CaCO₃(s). Thus, metabolism, photosynthesis, mineralization and geological process are the major chemical processes in the global carbon cycle.

Example 1

In general, it is known that rain water saturated with carbon dioxide has a pH of 5.6. Lower than 5.6 is called acid rain due to the presence of sulfur oxides and nitrogen oxides. Assume the water to be otherwise pure than the dissolved carbon dioxide, estimate the solubility of carbon dioxide in water?

Solution

Since pH = 5.6,

\[ [H+] = 10-5.6 M \notag \]
\[= 2.5\times 10^{-6} M \notag \]

Thus, the contribution of hydrogen ions from self ionization of water (pH = 7) is negligible. We have \([H^+] = 2.5 \times 10^{-6}\; M\) = \([HCO_3^-]\)

The ionization of dissolved carbon dioxide is represented by these reactions,

\[CO_2 + H_2O \rightarrow H_2CO_3\notag \]

\[H_2CO_3 \rightarrow H^+ + HCO_3^- \;\; \; K_{a1} = 4.2 \times 10^{-7}\notag \]

\[HCO_3^- \rightarrow H^+ + CO_3^{2-} \;\;\; K_{a2} = 4.8 \times 10^{-11}\notag \]

The major contribution to the production of hydrogen ion comes from the first ionization of H₂CO₃, and other contributions are almost negligible. If we assume the concentration of H₂CO₃ to be x M in its ionization,

\[H_2CO_3 \rightarrow H^+ + HCO_3^- \;\;\; K_{a1} = 4.2 \times 10^{-7}\notag \]

then, by definition of K_a1 we have

\[\dfrac{(2.5\times 10^{-6)} }{x} = 4.2\times 10^{-7}\notag \]

Thus,

\[x = 1.5 \times 10^{-5}\; M\notag \]
= 0.65 mg / L

Thus, the solubility is about 0.65 ppm by weight.

DISCUSSION
Many assumptions have been made here, other wise the solution will be more complicated. Make sure you understand the assumptions.

Example 2

From the solubility products of \(CaCO_3\), estimate its molar solubility in natural water saturated with carbon dioxide at pH 5.6 and 298 K.

Solution

From the estimates given in Example 1, we still have to consider these equilibria:

\[H_2CO_3 \rightarrow H^+ + HCO_3^- \;\;\; K_{a1} = 4.2\times 10^{-7}\notag \]

\[HCO_3^- \rightarrow H^+ + CO_3^{2-} \;\;\; K_{a2} = 4.8\times 10^{-11}\notag \]

Since the second ionization constant K_a2 << K_a1, it is safe to assume the following:

\[[H+] = [HCO3-] = 2.5\times 10^{-6} M\notag \]

in the above equilibria. The following formulation is derived by the definition of K_a2:

[H⁺] [CO₃^2-] 2.5\times 10^{^-6 [CO₃^2-]
-------------- = -------------------- = 4.8\times 10^{-11}
[HCO₃^-] 2.5\times 10^{^-6

Thus, [CO₃^2-] = 4.8\times 10^{^-11.

By the definition of the solubility product,

\[CaCO_3 \rightarrow Ca^{2+} + CO_3^{2-} \;\;\; K_{sp} = 5\times 10^{-9}\]

we have

[Ca2+] = 5\times 10^{-9/4.8\times 10^{-11
= 100 M

DISCUSSION
This value is obviously too high and unreasonable. The result is certainly incorrect. Thus, we should re-examine the last assumption. As CaCO₃ dissolves, the concentration of carbonate ion also increase. If this concentration is high, then the contribution due to dissolved carbon dioxide is negligible. Effectively, we have [Ca²⁺] = [CO₃^2-] = y, and

\[y^2 = 5 \times 10^{-9}\notag \]

Thus,

y = 7\times 10^{-5 M = 0.007 g CaCO3 / L.

This results is obtained by ignoring the dissolved carbon dioxide. The true value is probably somewhere in between, because as calcium carbonates dissolves, the pH of the solution changes.

Questions

1. Skill - Explain the chemistry involved in the global carbon cycle.
2. Skill - Explain and identify the chemical composition of minerals and ores.
3. Skill - Explain the meaning of a scientific datum, K_sp in plain language.
4. Skill - Describe the trend of a chemical property when a variable changes.

Solutions

1. Metabolism, photosynthesis, and mineralization are the major chemical processes.
2. Calcium carbonate
3. Since Ksp for MgCO3 is larger, it is more soluble.
4. In general terms, the solubility of limestone decreases as pH increases.

Contributors and Attributions

• Chung (Peter) Chieh (Professor Emeritus, Chemistry @ University of Waterloo)