18: Cooperativity

Last updated
Save as PDF

Page ID: 294350

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

It is often observed in molecular biology that nanoscale structures with sophisticated architectures assemble spontaneously, without the input of external energy. The behavior is therefore governed by physical principles that we can describe with thermodynamics and statistical mechanics. Examples include:

Protein and RNA folding
DNA hybridization
Assembly of protein complexes and viral capsids
Micelle and vesicle formation

Although each of these processes has distinct characteristics, they can be broadly described as self-assembly processes.

A characteristic of self-assembly is that it appears thermodynamically and kinetically as a simple “two-state transition”, even if thousands of atomic degrees of freedom are involved. That is, as one changes thermodynamic control variables such as temperature, one experimentally observes an assembled state and a disassembled state, but rarely an intermediate, partially assembled state. Furthermore, small changes in these thermodynamic variables can lead to dramatic changes, i.e., melting of DNA or proteins over a few degrees. This binary or switch-like behavior is very different from the smoothly varying unfolding curves we derived for simple lattice models of polymers.

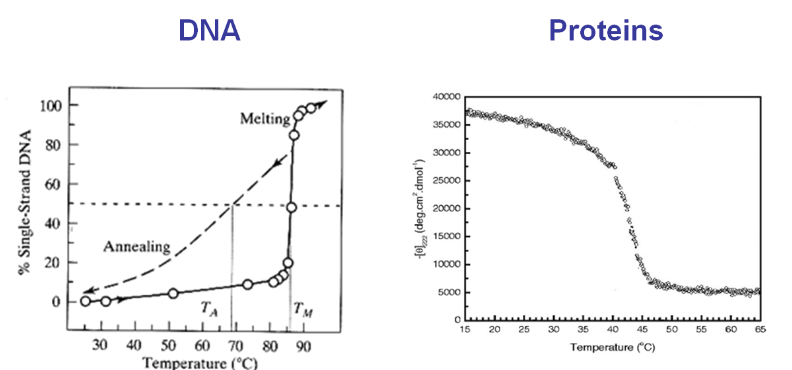
Phase transitions and phase equilibria are related phenomena described by the presence (or coexistence) of two states. These manifest themselves as a large change in the macroscopic properties of the system with only small changes in temperature or other thermodynamic variables. Heating liquid water from 99 °C to 101 °C has a profound effect on the density, which a 2° change at 25 °C would not have.

Such a “first-order” phase transition arises from a discontinuity in the free energy as a function of an intensive thermodynamic variable.¹ The thermodynamic description of two-state behavior governing a phase transition is illustrated below for the equilibrium between phases A and B. The free-energy profile is plotted as a function of an order parameter, a variable that distinguishes the physical characteristics relevant to the change of phase. For instance for a liquid–gas-phase transition, the volume or density are order parameters that change dramatically. As the temperature is increased the free energy of each state, characterized by its free energy minimum (G_i), decreases smoothly and continuously. However, state B decreases more rapidly that state A. While state A is the global free-energy minimum at low temperatures, state B is at high temperature. The phases are at equilibrium with each other at the temperature where G_A = G_B.

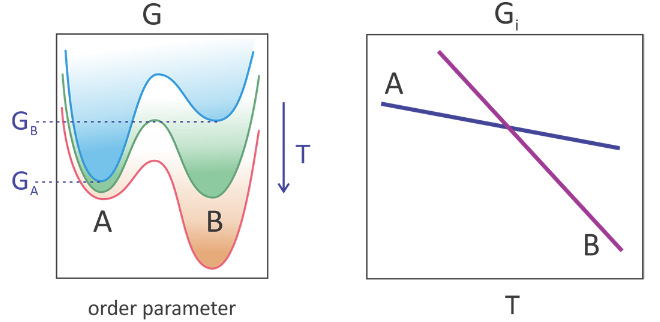
The presence of a phase transition is dependent on all molecules of the system changing state together, or cooperatively. In a first-order phase transition, this change is infinitely sharp or discontinuous, but the helix–coil transition and related cooperative phenomena can be continuous. Cooperativity is a term that can refer both to macroscopic phenomena and to a molecular scale. We use it to refer to many degrees of freedom changing concertedly. The size or number of particles or molecules participating in a cooperative process is the cooperative unit. In the case of a liquid–gas-phase transition, the cooperative unit is the macroscopic sample, whereas for protein folding it may involve most of the molecule.

What underlies cooperativity? We find that the free energy of the system is not simply additive in the parts. The energy of a particular configurational state depends on the configuration of its neighbors. For instance, the presence of one contact or molecular interaction increases or decreases the propensity for a second contact or interaction. We refer to this as positive or negative cooperativity. Beyond self-assembly, cooperativity plays a role in the binding of multiple ligands and allostery. Here we want to discuss the basic concepts relevant to cooperativity and its relationship to two-state behavior.

Based on observations we have previously made in other contexts, we can expect that cooperative behavior must involve competing thermodynamic effects. Structure is formed at the expense of a large loss of entropy, but the numerous favorable contacts that are formed lower the enthalpy even more. The free-energy change may be small, but this results from two opposing effects of large magnitude and opposite sign (H vs. TS). A small tweak in temperature can completely change the system.

________________________________________________

1. A first order transition is described as a discontinuity in ∂G/∂S or ∂G/∂V. A second order transition is one in which two phases merge into one at a critical point and is described by a discontinuity in the heat capacity or expansivity/compressibility of the system (∂S/∂T, ∂S/∂P, ∂V/∂T, or ∂V/∂P).