Direct Indicator Electrodes
- Page ID
- 78000
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The simplest type of direct indicator electrode is a metal, M, in contact with a solution containing its own cation, M+. At the metal-solution interface, a potential develops that is proportional to the activity of the metal ion in solution. The potential can be measured directly with respect to a reference electrode using the simple arrangement shown in Figure 1.
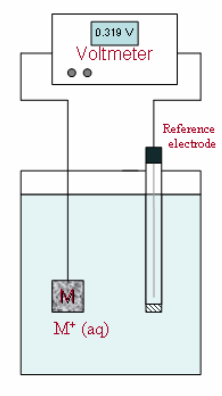
Figure 1. Electrochemical cell for a potentiometric measurement with a metallic indicator electrode.
The voltage measured is simply the difference between the potential at each electrode:
\[E_\ce{cell} = E_\ce{indicator} - E_\ce{reference} \tag{1}\]
Inert metal electrodes like Pt or Au can be used as indicator electrodes for ions involved in redox reactions that occur in solution but do not include the metallic form of the analyte.
Let’s discuss how a simple metal electrode can be used to measure the activity of its cation. This type of measurement is based on the fact that when a metal is in contact with a solution containing its cation, a potential develops. For example, when a piece of copper is placed in a copper sulfate solution:
The half-reaction is
\[\ce{Cu^2+}(aq) + 2e^- ↔ \ce{Cu}(s) \tag{2}\]
And the cell notation is
\[\ce{Cu}(s) / \ce{Cu^2+}(aq) \tag{3}\]
These types of electrodes develop an electrical potential in response to the equilibrium between the cation and metal surface, as shown in equation 2. The potential developed is proportional to analyte activity ( ACu2+ ) as determined from the Nernst Equation. For example, for the Cu(s) / Cu2+(aq) half cell:
\[E_{ind} = E^0_\mathrm{Cu^{2+}/Cu} − \dfrac{0.05916}{2} \log \dfrac{1}{A_\mathrm{Cu^{2+}}} = E^0_\mathrm{Cu^{2+}/Cu} + \dfrac{0.05916}{2} \log A_\mathrm{Cu^{2+}} \tag{4}\]
With a logarithmic dependence of potential on activity, it is convenient to express the analyte activity as a p-function (pCu = -log ACu2+ ). Substituting this relationship into equation 4 gives
\[E_{ind} = E^0_\mathrm{Cu^{2+}/Cu} - \dfrac{0.05916}{2} \mathrm{pCu} \tag{5}\]
In dilute solution of fixed ionic strength, we can assume that the analyte activity is approximately the same as its molar concentration, i.e. ACu2+ = [Cu2+] and that pCu is related to [Cu2+].
Let’s work on an example problem that shows the relationship between potential and analyte concentration.
Let’s put a metal electrode in solution with its mono-valent cation:
\[\ce{M+} (aq) + e^- ⇋ \ce{M}(s) \hspace{40px} E_{ind} = E^0_{ind} - 0.05916 \log(1/[\ce{M+}])\]
We can use a saturated calomel electrode (SCE) as a reference electrode:
\[\ce{\frac{1}{2} Hg2Cl2}(s) + e^- ⇋ \ce{Hg}(l) + \ce{Cl-} (aq) \hspace{40px} E_{ref} = \mathrm{0.241\: V}\]
The cell potential (or voltage you measure) is related to M+ concentration as defined by the Nernst Equation:
\[E_{cell} = E_{ind} - E_{ref} = E^0_{ind} - \mathrm{0.05916\log \left( \dfrac{1}{[M^+]} \right) - 0.241\: V}\]
Which reduces to:
\[E_{cell} = \left\{E^0_{ind} - 0.241\: \ce V\right\} + 0.05916 \log [\ce{M+}] = \left\{E^0_{ind} - 0.241\: \ce V\right\} - 0.05916\: p\ce{M}\]
What voltage change (in mV) would you expect for a 10X increase in cation concentration? What about a 100X increase?
Make your prediction and continue onto the next steps to see if you are correct . . .
Problem Exercise
Open up the following spreadsheet and follow the instructions below to see if your predictions are correct. Also try to answer the questions. Click here to open up the spreadsheet.
- Make sure that the sheet for the monovalent tab is showing.
- Enter a value for E0ind in the pink box. For example, E0 = +0.799 V for the Ag+/Ag system and E0 = +0.337 V for the Cu2+/Cu system.
- Enter a range of concentration values for the cation in the yellow boxes. Use the range from 5.00 x 10-6 to 1.00 x 10-3M.
- Inspect the graph that is generated from your values and answer the following questions.
- What is the voltage change for in 10X increase in cation activity? Was your prediction correct?
- What is the voltage change for in 100X increase in cation activity? Was your prediction correct?
- What do you predict is the slope of the line in the plot?
- Create a trendline by right-clicking on the data points and choosing “Add trendline” in the menu. Under the Type tab, make sure that “linear” is highlighted. Under the Options tab, click on the box next to “Display equation on chart”. Click OK. Was your prediction correct for the slope of the line?
- Repeat steps 2-8 for creating a plot in the “divalent” tab.
Summary
When making a potentiometric measurement, we do not want the measurement itself to alter potential. Therefore the following conditions must be met:
- Little to no current is passed through the cell.
- There is no net reaction.
- An equilibrium (static) measurement is made.
Direct indicator electrodes can experience interference from more easily reduced cations, thus decreasing their selectivity. Some metals used as the indicator electrode can be oxidized. Therefore, they are not as widely used as the next type of indicator electrodes – membrane electrodes, also referred to as ion-selective electrodes (ISE’s).


