pH / Ion Selective Electrodes
- Page ID
- 226219
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Because H+ binds more strongly than Na+ to the –SiO- function in glass, the H+ will displace more Na+. As the sample becomes more acidic, there are more H+ present. This greater H+ concentration will displace more Na+ from the hydrated gel.
Q2: What do you think is meant by mobility of ions?
Students will usually consider Mobility to mean how well something moves around. The mobility of ions can be defined as the rate at which they move around.
The smaller an object is the more mobile it will tend to be. For ions the mobility will be based on its effective ionic radius.
This is a challenging question – based on effective ionic radii in water, Na+ is smaller, so it should have a higher mobility in solution, but not necessarily in glass membrane. H+ is smaller than Na+, so it would have a higher mobility in glass.
Q4: Do you think other cations (e.g., Li+. K+) may have some ability to migrate into the hydrated gel layer of a pH electrode? If so, is this a problem?
Yes they will be able to migrate into the gel layer. This can cause a problem in that those ions will also displace Na+ giving rise to a higher membrane potential. This is a cause of the sodium error in pH measurements.
For the Na+ ion selective electrode, the varying junction potential only depends on the concentration of Na+.
It should be noted that liquid junction potentials will happen whenever two different electrolytes come in contact. Thus in the combination pH electrode, a potential can arise at the frit between the electrode and the solution. This junction potential arises due to the difference in mobility as the electrolyte moves across the boundary. This potential can be difficult to reproduce or known with any accuracy.
In solutions with a very low ionic strength, e.g. the surface waters of interest in the salmon declines, there is greater driving force for diffusion across the frit. Thus the propensity for junction potential errors becomes important to consider. This junction potential can be unstable, leading to drift; therefore periodic checks of the calibration (often hourly) may be needed. Calibration needs to be with low ionic strength buffers to better reflect the samples of interest, and make it so that the potential across the glass membrane is the only potential that is changing. It can also be important to note that the electrode design is important, therefore there are recommended electrodes for some types of environmental analyses when measuring surface or rain waters of low ionic strength.
This issue generally leads to a validation of the pH measurement by measuring the pH of distilled water that is in equilibrium with air. The pH should be around 5.7, thus pH readings should stabilize rather quickly between 5.6 and 5.8 to demonstrate the pH electrode is responding appropriately.
Q5: Consider a solution that has some Na+ and very high concentrations of K+Cl-. What effect do you think this might have on the activity of Na+ in the solution?
The high concentration of K+Cl- will affect the ionic strength of the solution, this will affect the activity coefficient of Na+. This can be calculated more formally using the extended Debye-Huckel equation (Equation 6.63 in the Harvey Analytical 2.0 text)
The relationship between activity and concentration for sodium is illustrated in Equation 2.
\[\mathrm{a_{Na}= γ_{Na} [Na^+]} \tag{2}\]
In eq 2, aNa is the sodium ion activity (mol L-1) , [Na+] is the sodium ion concentration (mol L-1), and γNa is the activity coefficient for the sodium ion. As we just discussed, as the sample ionic strength increases, there is a greater probability that analyte ions will interact with oppositely charged ions from the supporting electrolyte(s) dissolved in the sample. This effectively decreases the concentration of the “free ion”, which is represented by a decrease in the activity coefficient. As the ionic strength of a solution approaches zero, the activity coefficient approaches one, and under infinitely dilute conditions, the analyte activity and analyte concentration are equal. The relationship between the oxidized and reduced forms of sodium written as a reduction reaction can be described in Equation 3.
\[\ce{Na+ (aq) + e- → Na (s)} \tag{3}\]
The half-cell potential of the indicator electrode responds to changes in the activity of the analyte as described by the generalized form of the Nernst equation in Equation 4:
\[\mathrm{E_{ind}= E_{ind}^o- \dfrac{RT}{nF} \ln\left(\dfrac{1}{a_{Na}} \right)} \tag{4}\]
In eq 4, E° is the indicator electrode potential under standard conditions (298 K, 1.00 M Na+), R is the molar gas constant (8.314 J K-1 mol-1) , T is the absolute temperature (K) , n is the number of moles of electrons in the half-reaction, and F is Faraday’s constant (96485 C mol-1).
Q6: If the indicator electrode potential under standard conditions is -0.100 V, what is the indicator electrode potential at 298 K if the activity of the sodium ion is 0.10 M?
\[\mathrm{E_{ind}= -0.100\:V- \dfrac{ \dfrac{8.314\:J}{K\:mol}\times 298\:K}{1\:mol\: e^- \times \dfrac{96485\:C}{mol}} \ln \left(\dfrac{1}{0.1\:M}\right)}\nonumber\]
Therefore Eind = -0.1591 V
Q7: How does the indicator electrode potential change in the previous question if the temperature is increased by 10 degrees?
\[\mathrm{E_{ind}= -0.100\:V- \dfrac{\dfrac{8.314\:J}{K\:mol}\times 308\:K}{1\:mol\: e^- \times\dfrac{96485\:C}{mol}} \ln\left(\dfrac{1}{0.1\:M}\right)}\nonumber\]
Therefore Eind = -0.1611 V
Thus the measured potential is dependent on the temperature. This temperature effect has led to most meters have an automatic temperature correction.
Q8: How would you go about calibrating a sodium ion selective electrode?
You basically have to measure the response as a function of concentration. There are several practical ways that this is done. Most ISE are standardized by doing standard addition, where you start with distilled water and ionic strength adjuster. You then add increments of the analyte to the solution and measure the potential for each step.
The electrode could be also be calibrated using different solutions of known concentration (similar to how the pH electrode is calibrated using at least two solutions of known pH).
Q9: Can you think of a way to mitigate possible effects of ionic strength to insure that your calibration procedure and sample analysis provide an accurate measurement of the concentration of Na+ in the unknown?
The ionic strength needs to be rather constant, so the ionic strength is adjusted using the addition of an ionic strength adjuster solution. This solution contains a high concentration of ions that do not interfere or mask the indicator electrode response.
Q10: Would this proposed way to mitigate possible effects of ionic strength be utilized in pH measurements?
The ionic strength adjustor solution would have to have species that would not affect pH, thus greatly limiting the possible solution. In, practice this does not work well for measuring pH, as most ionic strength adjustments will have trace contamination that will affect pH, or the cations will introduce additional errors when the cation interacts with the glass membrane (the source of the Na+ error in pH measurements).
Q11: In the potentiometric determination of sodium ion of a mineral water sample, indicate if either of the following supporting electrolytes can be used for ionic strength adjustment: a 4.0M NH3 – NH4Cl buffer (pH 10) or 4.0M NaCl.
The 4.0 M NaCl would introduce sodium ions into the solution, which affects the concentration of what you are trying to measure. Therefore the ammonia buffer solution would be able to be used for the ionic strength adjuster.
Q12: What would be the general criteria you would need to use in selecting a suitable supporting electrolyte for an analysis using an ion selective electrode?
You want a supporting electrolyte that:
- Is different than analyte.
- Will not interfere with the concentration of the analyte (it does not react or bind with the analyte)
- It will not mask the presence of the analyte
- The indicator electrode does not respond to it.
- It will not foul the electrode or any electrode junction.
Q13: Based on the relationship in eq 6, how would you construct a calibration that links the changes in electrode potential to changes in the concentration of the sodium ion?
In the Nernst equation (eq 6) the cell potential varies with the log of the activities. The measured electrode potential is graphed versus the log of the concentration. The line of best fit is linear. The equation of the line of best fit is used to determine the concentration of the unknown.
Q14: What is the expected slope of a potentiometric calibration curve for sodium at 35°C? What effect does temperature have on the slope of a potentiometric calibration curve?
\[\mathrm{E_{ind}= E^0-\dfrac{\dfrac{8.314\:J}{K\:mol}\times 308\:K}{1\:mol\: e^-\times\dfrac{96485\:C}{mol}} 2.303 \log(Na^+)}\nonumber\]
If you plot the potential as a function of log concentration then the slope would be 0.0611 since ln x = 2.303 log x
Q15: If a sample has a sodium concentration of 1.0 x 10-3 M, and the sodium ISE has a selectivity coefficient of KNa,H = 30, what sample pH would cause a 1% error in the sodium ISE response?
First calculate the Eind for the solution of 1.0 x 10-3 M
\[\mathrm{E_{ind}=-.100\:V- \dfrac{0.05915}{1\:mol} \log\{1\times10^{-3} \}}\nonumber\]
\[\mathrm{E_{ind}=0.07745\:V}\nonumber\]
A 1% error in the response would give a
\[\mathrm{E_{ind}=0.07822\:V}\nonumber\]
Putting this back into the original equation
\[\mathrm{0.07822\:V=-.100\:V- \dfrac{0.05915}{1\:mol} \log\{x\}}\nonumber\]
Thus x = 0.0476
Putting this into
\[\mathrm{0.0476=\{a_{Analyte}+ K_{Analyte,Interferent} (a_{Interferent} )^{n_{Analyte}⁄n_{Interferent}} \}}\nonumber\]
\[\mathrm{0.0476=\{1\times10^{-3}+ 30(a_{Interferent} )^1 \}}\nonumber\]
Leads to an H+ concentration of 0.00155, or pH 2.8
Q16: Evaluate whether it is best to use alkaline or acidic conditions to determine the sodium ion concentration by ISE?
You want the alkaline conditions, as in acidic conditions you have a higher H+ activity, leading to a higher % error.
Q17: The table below contains sodium ISE calibration data. If the cell potential measured in a sample is ‑0.115 V, determine the sodium concentration (mol L-1) in this sample.
|
[Na+] (M) |
Ecell (V vs SCE) |
|---|---|
|
1.0 x 10-4 |
-0.221 |
|
1.0 x 10-3 |
-0.164 |
|
1.0 x 10-2 |
-0.107 |
|
1.0 x 10-1 |
-0.048 |
In Excel the graph would look like:
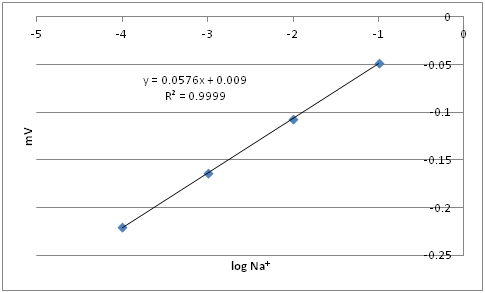
The line of best fit is -0.115V = 0.0576x +0.009
The log of Na+ is -2.152
Thus the concentration of Na+ is 7.0 x 10 -3 M
Q18: In the previous question, the sample was prepared by pipetting 5.00 mL of the original water sample and 2.00 mL of an ionic strength adjustment buffer into a 100 mL volumetric flask and diluting to the mark with distilled water. Determine the sodium concentration (mol L-1) in the original water sample.
\[C_1\times \mathrm{5.00\:mL= 7.0\times 10^{-3}\: M \times 100\:mL}\nonumber\]
Thus the original concentration is 0.14M


