9.1: Interferometry
- Page ID
- 55935
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Application of Vertical Scanning Interferometry to the Study of Crystal Surface Processes
The processes which occur at the surfaces of crystals depend on many external and internal factors such as crystal structure and composition, conditions of a medium where the crystal surface exists and others. The appearance of a crystal surface is the result of complexity of interactions between the crystal surface and the environment. The mechanisms of surface processes such as dissolution or growth are studied by the physical chemistry of surfaces. There are a lot of computational techniques which allows us to predict the changing of surface morphology of different minerals which are influenced by different conditions such as temperature, pressure, pH and chemical composition of solution reacting with the surface. For example, Monte Carlo method is widely used to simulate the dissolution or growth of crystals. However, the theoretical models of surface processes need to be verified by natural observations. We can extract a lot of useful information about the surface processes through studying the changing of crystal surface structure under influence of environmental conditions. The changes in surface structure can be studied through the observation of crystal surface topography. The topography can be directly observed macroscopically or by using microscopic techniques. Microscopic observation allows us to study even very small changes and estimate the rate of processes by observing changing the crystal surface topography in time.
Much laboratory worked under the reconstruction of surface changes and interpretation of dissolution and precipitation kinetics of crystals. Invention of AFM made possible to monitor changes of surface structure during dissolution or growth. However, to detect and quantify the results of dissolution processes or growth it is necessary to determine surface area changes over a significantly larger field of view than AFM can provide. More recently, vertical scanning interferometry (VSI) has been developed as new tool to distinguish and trace the reactive parts of crystal surfaces. VSI and AFM are complementary techniques and practically well suited to detect surface changes.
VSI technique provides a method for quantification of surface topography at the angstrom to nanometer level. Time-dependent VSI measurements can be used to study the surface-normal retreat across crystal and other solid surfaces during dissolution process. Therefore, VSI can be used to directly and nondirectly measure mineral dissolution rates with high precision. Analogically, VSI can be used to study kinetics of crystal growth.
Physical Principles of Optical Interferometry
Optical interferometry allows us to make extremely accurate measurements and has been used as a laboratory technique for almost a hundred years. Thomas Young observed interference of light and measured the wavelength of light in an experiment, performed around 1801. This experiment gave an evidence of Young's arguments for the wave model for light. The discovery of interference gave a basis to development of interferomertry techniques widely successfully used as in microscopic investigations, as in astronomic investigations.
The physical principles of optical interferometry exploit the wave properties of light. Light can be thought as electromagnetic wave propagating through space. If we assume that we are dealing with a linearly polarized wave propagating in a vacuum in z direction, electric field E can be represented by a sinusoidal function of distance and time.
\[ E(x,y,z,t)\ =\ a \cos[2\pi (vt\ -\ z/\lambda )] \label{1} \]
Where a is the amplitude of the light wave, v is the frequency, and λ is its wavelength. The term within the square brackets is called the phase of the wave. Let’s rewrite this equation in more compact form,
\[ E(x,y,z,t)\ =\ a \cos(\omega t\ -\ kz) \label{2} \]
where ω=2πv is the circular frequency, and k=2π/λ is the propagation constant. Let’s also transform this second equation into a complex exponential form,
\[ E(x,y,z,t)\ =\ Re(a\ e^{i(\psi + \omega t)})\ =\ Re(a\ e^{i\omega t}) \label{3} \]
where ϕ=2πz/λ and A=e−iϕ is known as the complex amplitude. If n is a refractive index of a medium where the light propagates, the light wave traverses a distance d in such a medium. The equivalent optical path in this case is
\[ p\ =\ n\ \cdot \ d \label{4} \]
When two light waves are superposed, the result intensity at any point depends on whether reinforce or cancel each other (Figure \(\PageIndex{1}\)). This is well known phenomenon of interference. We will assume that two waves are propagating in the same direction and are polarized with their field vectors in the same plane. We will also assume that they have the same frequency. The complex amplitude at any point in the interference pattern is then the sum of the complex amplitudes of the two waves, so that we can write,
\[ A\ =\ A_{1}\ +\ A_{2} \label{5} \]
where A1=a1exp(−iϕ1) and A2=a2exp(−iϕ2) are the complex amplitudes of two waves. The resultant intensity is, therefore,
\[ I\ =\ |A|^{2}\ =\ I_{1}\ +\ I_{2}\ +\ 2(I_{1}I_{2})^{1/2} cos (\Delta \psi) \label{6} \]
where I1 and I2 are the intensities of two waves acting separately, and Δϕ=ϕ1−ϕ2 is the phase difference between them. If the two waves are derived from a common source, the phase difference corresponds to an optical path difference,
\[ \Delta p\ =\ (\lambda /2 \pi) \Delta \psi \label{7} \]

If Δϕ, the phase difference between the beams, varies linearly across the field of view, the intensity varies cosinusoidally, giving rise to alternating light and dark bands or fringes (Figure \(\PageIndex{1}\)). The intensity of an interference pattern has its maximum value:
\[ I_{max}\ =\ I_{1}\ +\ I_{2}\ +\ 2(I_{1}I_{2})^{1/2} \label{8} \]
when Δϕ=2mπ, where m is an integer and its minimum value i determined by:
\[ I_{min}\ =\ I_{1}\ +\ I_{2}\ -\ 2(I_{1}I_{2})^{1/2} \label{9} \]
when Δϕ=(2m+1)π The principle of interferometry is widely used to develop many types of interferometric set ups. One of the earliest set ups is Michelson interferometry. The idea of this interferometry is quite simple: interference fringes are produced by splitting a beam of monochromatic light so that one beam strikes a fixed mirror and the other a movable mirror. An interference pattern results when the reflected beams are brought back together. The Michelson interferometric scheme is shown in Figure \(\PageIndex{2}\).
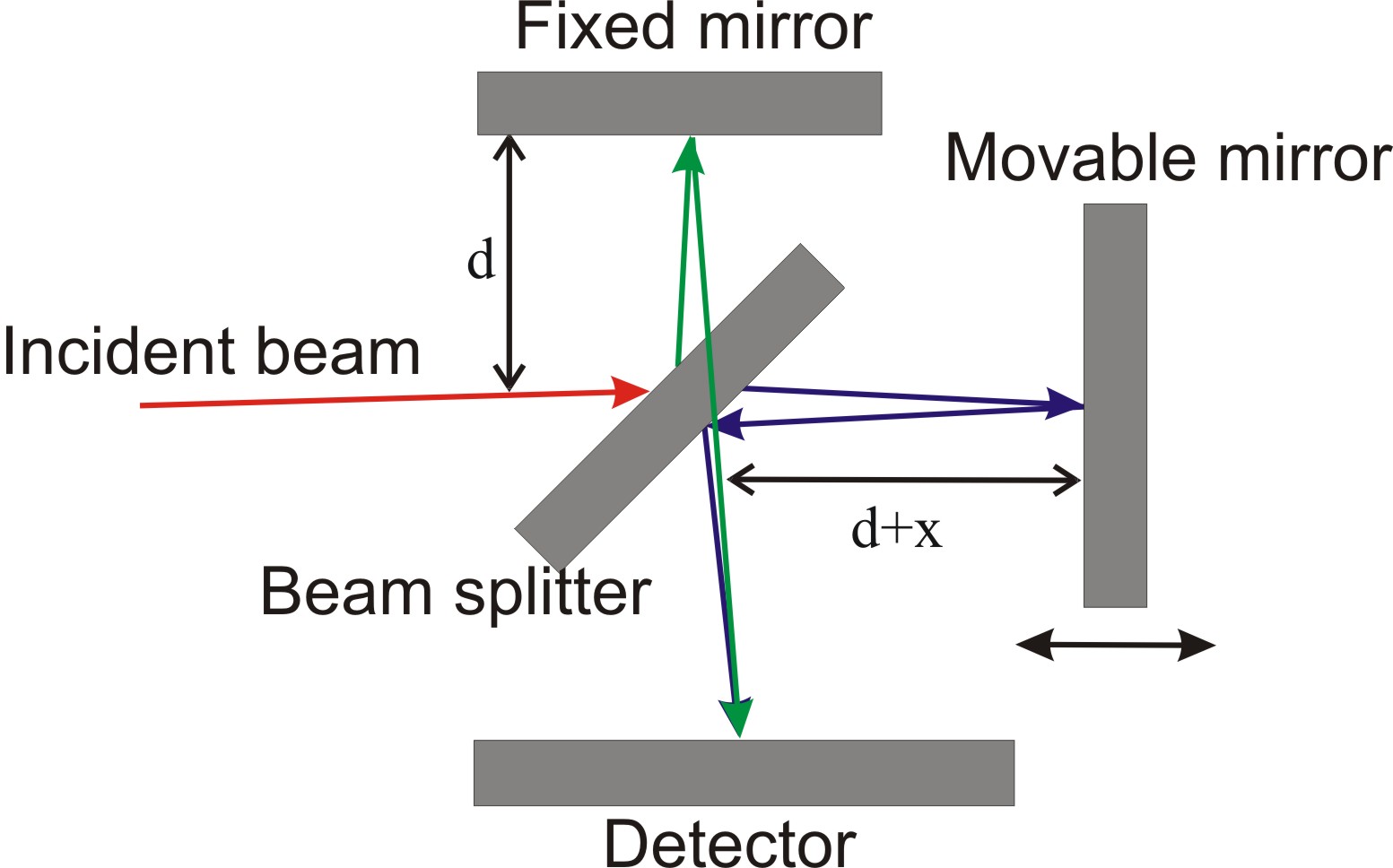
The difference of path lengths between two beams is 2x because beams traverse the designated distances twice. The interference occurs when the path difference is equal to integer numbers of wavelengths,
\[ \Delta p\ =\ 2x\ m\lambda (m= 0, \pm 1, \pm 2 ... ) \label{10} \]
Modern interferometric systems are more complicated. Using special phase-measurement techniques they capable to perform much more accurate height measurements than can be obtained just by directly looking at the interference fringes and measuring how they depart from being straight and equally spaced. Typically interferometric system consist of lights source, beamsplitter, objective system, system of registration of signals and transformation into digital format and computer which process data. Vertical scanning interferometry is contains all these parts. Figure \(\PageIndex{3}\) shows a configuration of a VSI interferometric system.
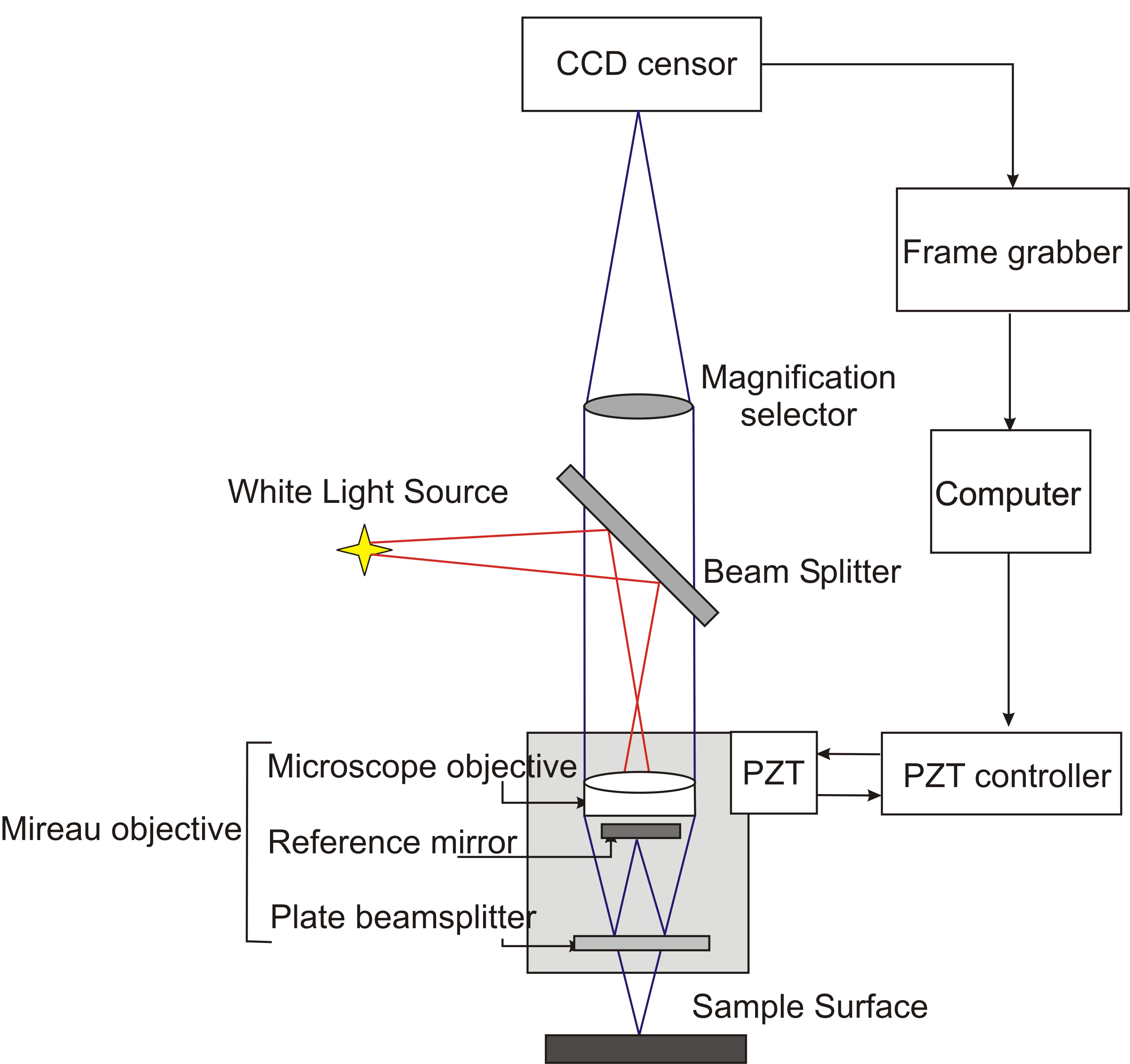
Many of modern interferometric systems use Mirau objective in their constructions. Mireau objective is based on a Michelson interferometer. This objective consists of a lens, a reference mirror and a beamsplitter. The idea of getting interfering beams is simple: two beams (red lines) travel along the optical axis. Then they are reflected from the reference surface and the sample surface respectively (blue lines). After this these beams are recombined to interfere with each other. An illumination or light source system is used to direct light onto a sample surface through a cube beam splitter and the Mireau objective. The sample surface within the field of view of the objective is uniformly illuminated by those beams with different incidence angles. Any point on the sample surface can reflect those incident beams in the form of divergent cone. Similarly, the point on the reference symmetrical with that on the sample surface also reflects those illuminated beams in the same form.
The Mireau objective directs the beams reflected of the reference and the sample surface onto a CCD (charge-coupled device) sensor through a tube lens. The CCD sensor is an analog shift register that enables the transportation of analog signals (electric charges) through successive stages (capacitors), controlled by a clock signal. The resulting interference fringe pattern is detected by CCD sensor and the corresponding signal is digitized by a frame grabber for further processing with a computer.
The distance between a minimum and a maximum of the interferogram produced by two beams reflected from the reference and sample surface is known. That is, exactly half the wavelength of the light source. Therefore, with a simple interferogram the vertical resolution of the technique would be also limited to λ/2. If we will use a laser light as a light source with a wavelength of 300 nm the resolution would be only 150 nm. This resolution is not good enough for a detailed near-atomic scale investigation of crystal surfaces. Fortunately, the vertical resolution of the technique can be improved significantly by moving either the reference or the sample by a fraction of the wavelength of the light. In this way, several interferograms are produced. Then they are all overlayed, and their phase shifts compared by the computer software Figure. This method is widely known as phase shift interferometry (PSI).

Most optical testing interferometers now use phase-shifting techniques not only because of high resolution but also because phase-shifting is a high accuracy rapid way of getting the interferogram information into the computer. Also usage of this technique makes the inherent noise in the data taking process very low. As the result in a good environment angstrom or sub-angstrom surface height measurements can be performed. As it was said above, in phase-shifting interferometry the phase difference between the interfering beams is changed at a constant rate as the detector is read out. Once the phase is determined across the interference field, the corresponding height distribution on the sample surface can be determined. The phase distribution \(φ(x, y)\) is recorded by using the CCD camera.
Let’s assign \(A(x, y)\), \(B(x, y)\), \(C(x, y)\) and \(D(x, y)\) to the resulting interference light intensities which are corresponded to phase-shifting steps of 0, π/2, π and 3π/2. These intensities can be obtained by moving the reference mirror through displacements of λ/8, λ/4 and 3λ/8, respectively. The equations for the resulting intensities would be:
\[ A(x,y)\ =\ I_{1}(x,y)\ +\ I_{2}(x,y) \cos(\alpha (x,y)) \label{11} \]
\[ B(x,y)\ =\ I_{1}(x,y)\ -\ I_{2}(x,y) \sin(\alpha (x,y)) \label{12} \]
\[ C(x,y)\ =\ I_{1}(x,y)\ -\ I_{2}(x,y) \cos(\alpha (x,y)) \label{13} \]
\[ D(x,y)\ =\ I_{1}(x,y)\ +\ I_{2}(x,y) \sin(\alpha (x,y)) \label{14} \]
where \(I_1(x,y)\) and \(I_2(x,y)\) are two overlapping beams from two symmetric points on the test surface and the reference respectively. Solving Equations \ref{11} - \ref{14}, the phase map \(φ(x, y)\) of a sample surface will be given by the relation:
\[ \psi (x,y)\ =\ \frac{B(x,y)\ -\ D(x,y)}{A(x,y)\ -\ C(x,y)} \label{15} \]
Once the phase is determined across the interference field pixel by pixel on a two-dimensional CCD array, the local height distribution/contour, \(h(x, y)\), on the test surface is given by
\[ h(x,y)\ =\ \frac{\lambda}{4\pi } \psi (x,y) \label{16} \]
Normally the resulted fringe can be in the form of a linear fringe pattern by adjusting the relative position between the reference mirror and sample surfaces. Hence any distorted interference fringe would indicate a local profile/contour of the test surface.
It is important to note that the Mireau objective is mounted on a capacitive closed-loop controlled PZT (piezoelectric actuator) as to enable phase shifting to be accurately implemented. The PZT is based on piezoelectric effect referred to the electric potential generated by applying pressure to piezoelectric material. This type of materials is used to convert electrical energy to mechanical energy and vice-versa. The precise motion that results when an electric potential is applied to a piezoelectric material has an importance for nanopositioning. Actuators using the piezo effect have been commercially available for 35 years and in that time have transformed the world of precision positioning and motion control.
Vertical scanning interferometer also has another name; white-light interferometry (WLI) because of using the white light as a source of light. With this type of source a separate fringe system is produced for each wavelength, and the resultant intensity at any point of examined surface is obtained by summing these individual patterns. Due to the broad bandwidth of the source the coherent length L of the source is short:
\[ L\ =\ \frac{\lambda ^{2}}{n \Delta \lambda} \label{17} \]
where λ is the center wavelength, n is the refractive index of the medium, ∆λ is the spectral width of the source. In this way good contrast fringes can be obtained only when the lengths of interfering beams pathways are closed to each other. If we will vary the length of a pathway of a beam reflected from sample, the height of a sample can be determined by looking at the position for which a fringe contrast is a maximum. In this case interference pattern exist only over a very shallow depth of the surface. When we vary a pathway of sample-reflected beam we also move the sample in a vertical direction in order to get the phase at which maximum intensity of fringes will be achieved. This phase will be converted in height of a point at the sample surface.
The combination of phase shift technology with white-light source provides a very powerful tool to measure the topography of quite rough surfaces with the amplitude in heights about and the precision up to 1-2 nm. Through a developed software package for quantitatively evaluating the resulting interferogram, the proposed system can retrieve the surface profile and topography of the sample objects Figure \(\PageIndex{5}\).

A Comparison of Common Methods to Determine Surface Topography: SEM, AFM and VSI
Except the interferometric methods described above, there are a several other microscopic techniques for studying crystal surface topography. The most common are scanning electron microscopy (SEM) and atomic force microscopy (AFM). All these techniques are used to obtain information about the surface structure. However they differ from each other by the physical principles on which they based.
Scanning Electron Microscopy
SEM allows us to obtain images of surface topography with the resolution much higher than the conventional light microscopes do. Also it is able to provide information about other surface characteristics such as chemical composition, electrical conductivity etc, see Figure \(\PageIndex{6}\). All types of data are generated by the reflecting of accelerated electron beams from the sample surface. When electrons strike the sample surface, they lose their energy by repeated random scattering and adsorption within an outer layer into the depth varying from 100 nm to 5 microns.
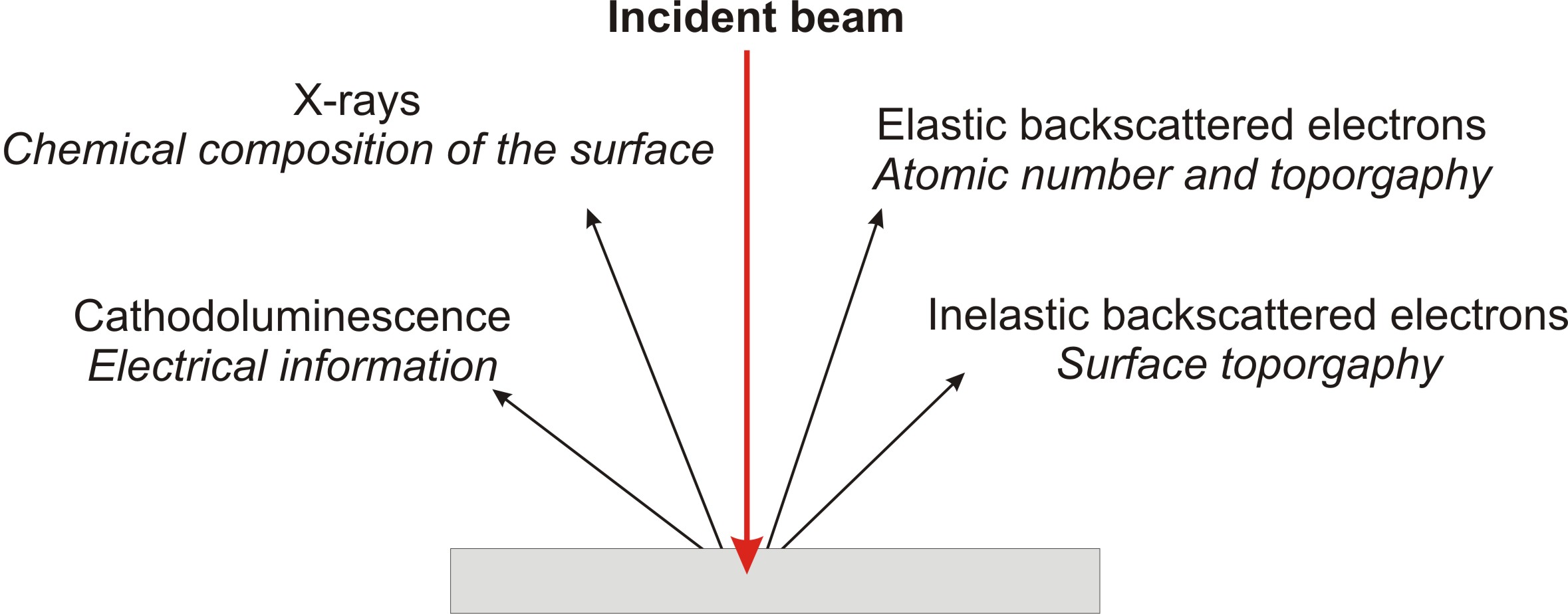
The thickness of this outer layer also knows as interactive layer depends on energy of electrons in the beam, composition and density of a sample. Result of the interaction between electron beam and the surface provides several types of signals. The main type is secondary or inelastic scattered electrons. They are produced as a result of interaction between the beam of electrons and weakly bound electrons in the conduction band of the sample. Secondary electrons are ejected from the k-orbitals of atoms within the surface layer of thickness about a few nanometers. This is because secondary electrons are low energy electrons (<50 eV), so only those formed within the first few nanometers of the sample surface have enough energy to escape and be detected. Secondary backscattered electrons provide the most common signal to investigate surface topography with lateral resolution up to 0.4 - 0.7 nm.
High energy beam electrons are elastic scattered back from the surface. This type of signal gives information about chemical composition of the surface because the energy of backscattered electrons depends on the weight of atoms within the interaction layer. Also this type of electrons can form secondary electrons and escape from the surface or travel father into the sample than the secondary. The SEM image formed is the result of the intensity of the secondary electron emission from the sample at each x,y data point during the scanning of the surface.
Atomic Force Microscopy
AFM is a very popular tool to study surface dissolution. AFM set up consists of scanning a sharp tip on the end of a flexible cantilever which moves across a sample surface. The tips typically have an end radius of 2 to 20 nm, depending on tip type. When the tip touch the surface the forces of these interactions leads to deflection of a cantilever. The interaction between tip and sample surface involve mechanical contact forces, van der Waals forces, capillary forces, chemical bonding, electrostatic forces, magnetic forces etc. The deflection of a cantilever is usually measured by reflecting a laser beam off the back of the cantilever into a split photodiode detector. A schematic drawing of AFM can be seen in Figure \(\PageIndex{7}\). The two most commonly used modes of operation are contact mode AFM and tapping mode AFM, which are conducted in air or liquid environments.

Working under the contact mode AFM scans the sample while monitoring the change in cantilever deflection with the split photodiode detector. Loop maintains a constant cantilever reflection by vertically moving the scanner to get a constant signal. The distance which the scanner goes by moving vertically at each x,y data point is stored by the computer to form the topographic image of the sample surface. Working under the tapping mode AFM oscillates the cantilever at its resonance frequency (typically~300 kHz) and lightly “taps” the tip on the surface during scanning. The electrostatic forces increase when tip gets close to the sample surface, therefore the amplitude of the oscillation decreases. The laser deflection method is used to detect the amplitude of cantilever oscillation. Similar to the contact mode, feedback loop maintains a constant oscillation amplitude by moving the scanner vertically at every x,y data point. Recording this movement forms the topographical image. The advantage of tapping mode over contact mode is that it eliminates the lateral, shear forces present in contact mode. This enables tapping mode to image soft, fragile, and adhesive surfaces without damaging them while work under contact mode allows the damage to occur.
Comparison of Techniques
All techniques described above are widely used in studying of surface nano- and micromorphology. However, each method has its own limitations and the proper choice of analytical technique depends on features of analyzed surface and primary goals of research.
All these techniques are capable to obtain an image of a sample surface with quite good resolution. The lateral resolution of VSI is much less, then for other techniques: 150 nm for VSI and 0.5 nm for AFM and SEM. Vertical resolution of AFM (0.5 Ǻ) is better then for VSI (1 - 2 nm), however VSI is capable to measure a high vertical range of heights (1 mm) which makes possible to study even very rough surfaces. On the contrary, AFM allows us to measure only quite smooth surfaces because of its relatively small vertical scan range (7 µm). SEM has less resolution, than AFM because it requires coating of a conductive material with the thickness within several nm.
The significant advantage of VSI is that it can provide a large field of view (845 × 630 µm for 10x objective) of tested surfaces. Recent studies of surface roughness characteristics showed that the surface roughness parameters increase with the increasing field of view until a critical size of 250,000 µm is reached. This value is larger then the maximum field of view produced by AFM (100 × 100 µm) but can be easily obtained by VSI. SEM is also capable to produce images with large field of view. However, SEM is able to provide only 2D images from one scan while AFM and VSI let us to obtain 3D images. It makes quantitative analysis of surface topography more complicated, for example, topography of membranes is studied by cross section and top view images.
| VSI | AFM | SEM | |
|---|---|---|---|
| Lateral resolution | 0.5 - 1.2µm | 0.5 nm | 0.5 - 1 nm |
| Vertical Resolution | 2 nm | 0.5 Å | Only 2D images |
| Field of View | 845 x 630 µm (10x objective) | 100 x 100 µm | 1 - 2 mm |
| Vertical Range of Scan | 1 mm | 10 µm | - |
| Preparation of Sample | - | - | Required coating of a conducted material |
| Required environment | Air | Air, liquid | Vacuum |
The Experimental Studying of Surface Processes Using Microscopic Techniques
The limitations of each technique described above are critically important to choose appropriate technique for studying surface processes. Let’s explore application of these techniques to study dissolution of crystals.
When crystalline matter dissolves the changes of the crystal surface topography can be observed by using microscopic techniques. If we will apply an unreactive mask (silicon for example) on crystal surface and place a crystalline sample into the experiment reactor then we get two types of surfaces: dissolving and remaining the same or unreacted. After some period of time the crystal surface starts to dissolve and change its z-level. In order to study these changes ex situ we can pull out a sample from the reaction cell then remove a mask and measure the average height difference Δh bar between the unreacted and dissolved areas. The average heights of dissolved and unreacted areas are obtained through digital processing of data obtained by microscopes. The velocity of normal surface retreat vSNR during the time interval ∆t is defined by \ref{18}
\[ \nu _{SNR}\ =\ \frac{\Delta \hbar}{\Delta t} \label{18} \]
Dividing this velocity by the molar volume (cm3/mol) gives a global dissolution rate in the familiar units of moles per unit area per unit time:
\[ R\ =\ \frac{\nu _{SNR}}{\bar{V}} \label{19} \]
This method allows us to obtain experimental values of dissolution rates just by precise measuring of average surface heights. Moreover, using this method we can measure local dissolution rates at etch pits by monitoring changes in the volume and density of etch pits across the surface over time. VSI technique is capable to perform these measurements because of large vertical range of scanning. In order to get precise values of rates which are not depend on observing place of crystal surface we need to measure enough large areas. VSI technique provides data from areas which are large enough to study surfaces with heterogeneous dissolution dynamics and obtain average dissolution rates. Therefore, VSI makes possible to measure rates of normal surface retreat during the dissolution and observe formation, growth and distribution of etch pits on the surface.
However, if the mechanism of dissolution is controlled by dynamics of atomic steps and kink sites within a smooth atomic surface area, the observation of the dissolution process need to use a more precise technique. AFM is capable to provide information about changes in step morphology in situ when the dissolution occurs. For example, immediate response of the dissolved surface to the changing of environmental conditions (concentrations of ions in the solution, pH etc.) can be studied by using AFM.
SEM is also used to examine micro and nanotexture of solid surfaces and study dissolution processes. This method allows us to observe large areas of crystal surface with high resolution which makes possible to measure a high variety of surfaces. The significant disadvantage of this method is the requirement to cover examine sample by conductive substance which limits the resolution of SEM. The other disadvantage of SEM is that the analysis is conducted in vacuum. Recent technique, environmental SEM or ESEM overcomes these requirements and makes possible even examine liquids and biological materials. The third disadvantage of this technique is that it produces only 2D images. This creates some difficulties to measure Δhbar within the dissolving area. One of advantages of this technique is that it is able to measure not only surface topography but also chemical composition and other surface characteristics of the surface. This fact is used to monitor changing in chemical composition during the dissolution.
Dual Polarization Interferometry for Thin Film Characterization
Overview
As research interests begin to focus on progressively smaller dimensions, the need for nanoscale characterization techniques has seen a steep rise in demand. In addition, the wide scope of nanotechnology across all fields of science has perpetuated the application of characterization techniques to a multitude of disciplines. Dual polarization interferometry (DPI) is an example of a technique developed to solve a specific problem, but was expanded and utilized to characterize fields ranging surface science, protein studies, and crystallography. With a simple optical instrument, DPI can perform label-free sensing of refractive index and layer thickness in real time, which provides vital information about a system on the nanoscale, including the elucidation of structure-function relationships.
History
DPI was conceived in 1996 by Dr. Neville Freeman and Dr. Graham Cross (Figure \(\PageIndex{8}\)) when they recognized a need to measure refractive index and adlayer thickness simultaneously in protein membranes to gain a true understanding of the dynamics of the system. They patented the technique in 1998, and the instrument was commercialized by Farfield Group Ltd. in 2000.

Freeman and Cross unveiled the first full publication describing the technique in 2003, where they chose to measure well-known protein systems and compare their data to X-ray crystallography and neutron reflection data. The first system they studied was sulpho-NHS-LC-biotin coated with streptavidin and a biotinylated peptide capture antibody, and the second system was BS3 coated with anti-HSA. Molecular structures are shown in Figure \(\PageIndex{9}\). Their results showed good agreement with known layer thicknesses, and the method showed clear advantages over neutron reflection and surface plasmon resonance. A schematic and picture of the instrument used by Freeman and Cross in this publication is shown in Figure \(\PageIndex{10}\) and Figure \(\PageIndex{11}\), respectively.
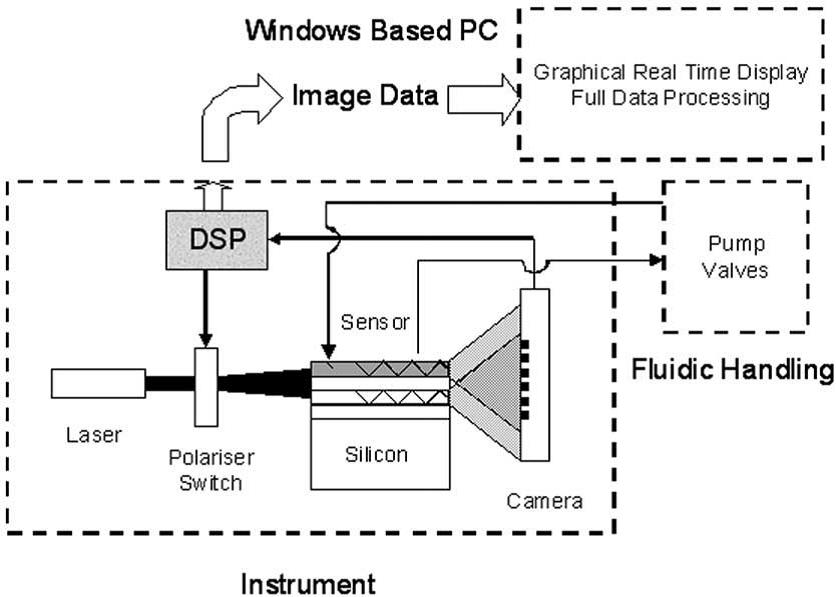

Instrumentation
Theory
The optical power of DPS comes from the ability to measure two different interference fringe patterns simultaneously in real time. Phase changes in these fringe patterns result from changes in refractive index and layer thickness that can be detected by the waveguide interferometer, and resolving these interference patterns provides refractive index and layer thickness values.
Optics
A representation of the interferometer is shown in Figure \(\PageIndex{12}\). The interferometer is composed of a simplified slab waveguide, which guides a wave of light in one transverse direction without scattering. A broad laser light is shone on the side facet of stacked waveguides separated with a cladding layer, where the waveguides act as a sensing layer and a reference layer that produce an interference pattern in a decaying (evanescent) electric field.
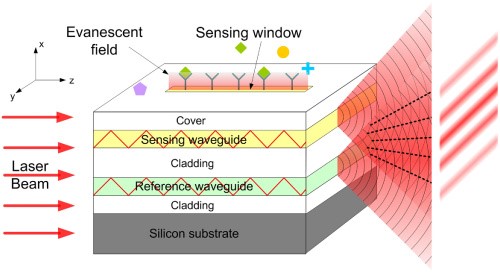
A full representation of DPI theory and instrumentation is shown in Figure \(\PageIndex{13}\) and Figure \(\PageIndex{14}\), respectively. The layer thickness and refractive index measurements are determined by measuring two phase changes in the system simultaneously because both transverse-electric and transverse-magnetic polarizations are allowed through the waveguides. Phase changes in each polarization of the light wave are lateral shifts of the wave peak from a given reference peak. The phase shifts are caused by changes in refractive index and layer thickness that result from molecular fluctuations in the sample. Switching between transverse-electric and transverse-magnetic polarizations happens very rapidly at 2 ms, where the switching mechanism is performed by a liquid crystal wave plate. This enables real-time measurements of the parameters to be obtained simultaneously.
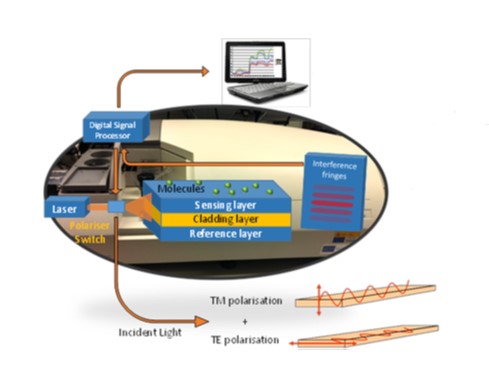
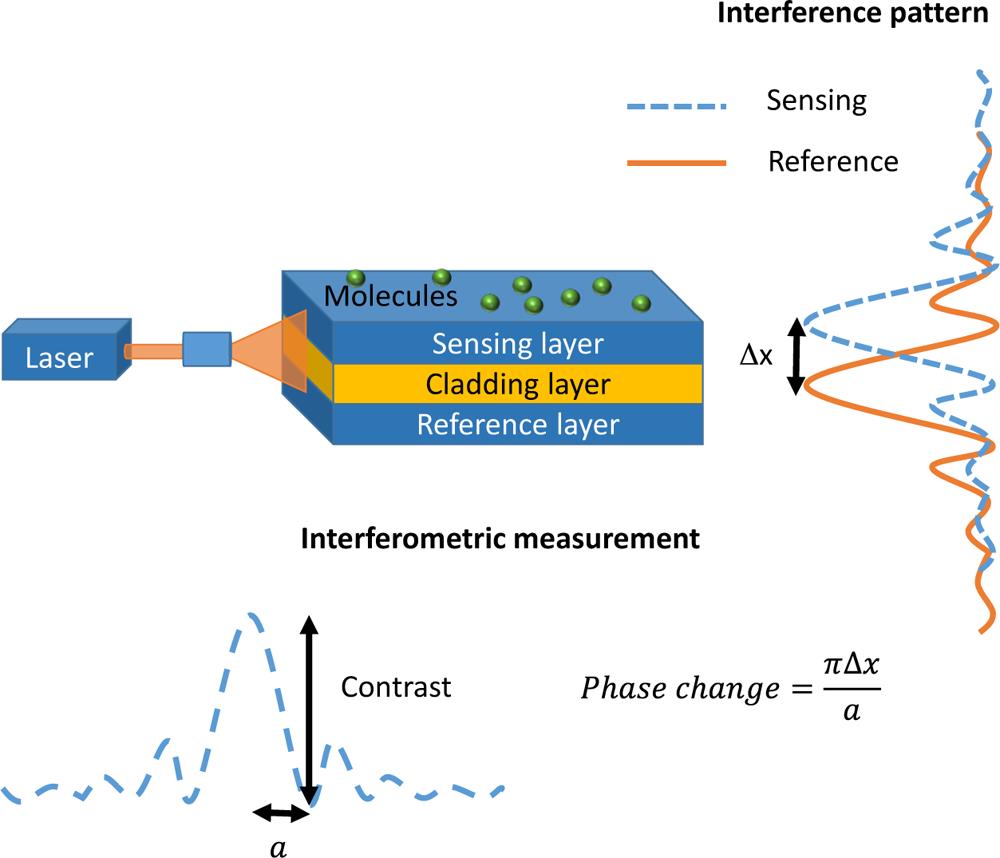
Comparison of DPI with Other Techniques
Initial DPI Evaluations
The first techniques rigorously compared to DPI were neutron reflection (NR) and X-ray diffraction. These studies demonstrated that DPI had a very high precision of 40 pm, which is comparable to NR and superior to X-ray diffraction. Additionally, DPI can provide real time information and conditions similar to an in-vivo environment, and the instrumental requirements are far simpler than those for NR. However, NR and X-ray diffraction are able to provide structural information that DPI cannot determine.
DPI Comparison with orthogonal Analytical Techniques
Comparisons between DPI and alternative techniques have been performed since the initial evaluations, with techniques including surface plasmon resonance (SPR), atomic force microscopy (AFM), and quartz crystal microbalance with dissipation monitoring (QCM-D).
SPR is well-established for characterizing protein adsorption and has been used before DPI was developed. These techniques are very similar in that they both use an optical element based on an evanescent field, but they differ greatly in the method of calculating the mass of adsorbed protein. Rigorous testing showed that both tests give very accurate results, but their strengths differ. Because SPR uses spot-testing with an area of 0.26 mm2 while DPI uses the average measurements over the length of the entire 15 mm chip, SPR is recommended for use in kinetic studies where diffusion in involved. However, DPI shows much greater accuracy than SPR when measuring refractive index and layer thickness.
Atomic Force Microscopy is a very different analytical technique than DPI because it is a type of microscopy used for high-resolution surface characterization. Hence, AFM and DPI are well-suited to be used in conjunction because AFM can provide accurate molecular structures and surface mapping while DPI provides layer thickness that AFM cannot determine.
QCM-D is a technique that can be used with DPI to provide complementary data. QCM-D differs from DPI by calculating both mass of the solvent and the mass of the adsorbed protein layer. These techniques can be used together to determine the amount of hydration in the adsorbed layer. QCM-D can also quantify the supramolecular conformation of the adlayer using energy dissipation calculations, while DPI can detect these conformational changes using birefringence, thus making these techniques orthogonal. One way that DPI is superior to QCM-D is that the latter techniques loses accuracy as the film becomes very thin, while DPI retains accuracy throughout the angstrom scale.
A tabulated representation of these techniques and their ability to measure structural detail, in-vivoconditions, and real time data is shown in Table \(\PageIndex{2}\).
| Technique | Real Time | Close to In-vivo | Structural Details |
|---|---|---|---|
| QCM-D | Yes | Yes | Medium |
| SPR | Yes | Yes | Low |
| X-ray | No | No | Very high |
| AFM | No | No | High |
| NR | No | Yes | High |
| DPI | Yes | Yes | Medium |
Applications of DPI
Protein Studies
DPI has been most heavily applied to protein studies. It has been used to elucidate membrane crystallization, protein orientation in a membrane, and conformational changes. It has also been used to study protein-protein interactions, protein-antibody interactions, and the stoichiometry of binding events.
Thin Film Studies
Since its establishment using protein interaction studies, DPI has seen its applications expanded to include thin film studies. DPI was compared to ellipsometry and QCM-D studies to indicate that it can be applied to heterogeneous thin films by applying revised analytical formulas to estimate the thickness, refractive index, and extinction coefficient of heterogeneous films that absorb light. A non-uniform density distribution model was developed and tested on polyethylenimine deposited onto silica and compared to QCD-M measurements. Additionally, this revised model was able to calculate the mass of multiple species of molecules in composite films, even if the molecules absorbed different amounts of light. This information is valuable for providing surface composition. The structure of polyethylenimine used to form an adsorbing film is shown in Figure \(\PageIndex{15}\).
A challenge of measuring layer thickness in thin films such as polyethylenimine is that DPI’s evanescent field will create inaccurate measurements in inhomogeneous films as the film thickness increases. An error of approximately 5% was seen when layer thickness was increased to 90 nm. Data from this study determining the densities throughout the polyethylenimine film are shown in Figure \(\PageIndex{16}\).
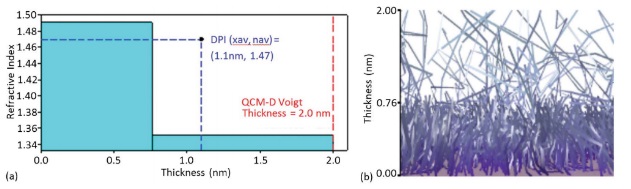
Thin Layer Adsorption Studies
Similar to thin film characterization studies, thin layers of adsorbed polymers have also been elucidated using DPI. It has been demonstrated that two different adsorption conformations of polyacrylamide form on resin, which provides useful information about adsorption behaviors of the polymer. This information is industrially important because polyacrylamide is widely used through the oil industry, and the adsorption of polyacrylamide onto resin is known to affect the oil/water interfacial stability.
Initial adsorption kinetics and conformations were also illuminated using DPI on bottlebrush polyelectrolytes. Bottlebrush polyelectrolytes are show in Figure \(\PageIndex{17}\). It was shown that polyelectrolytes with high charge density initially adsorbed in layers that were parallel to the surface, but as polyelectrolytes were replaced with low charge density species, alignment changed to prefer perpendicular arrangement to the surface.
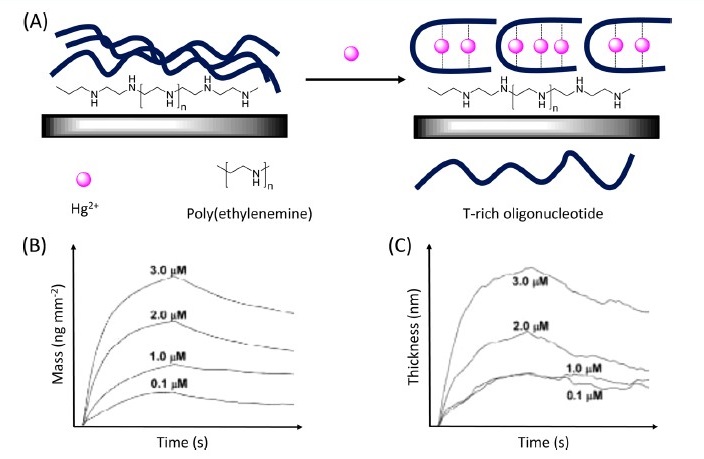
Hg2+ Biosensing Studies
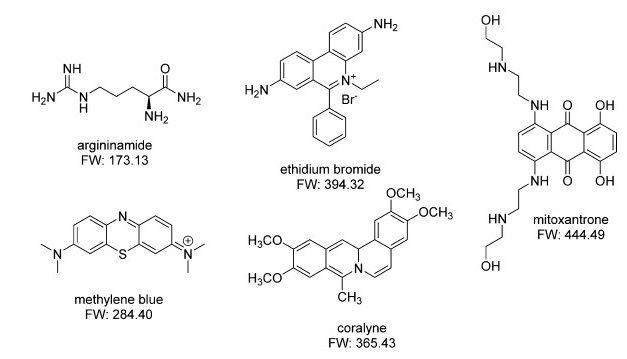
In 2009, it was shown by Wang et al. that DPI could be used for small molecule sensing. In their first study describing this use of DPI, they used single stranded DNA that was rich in thymine to complex Hg2+ ions. When DNA complexed with Hg2+, the DNA transformed from a random coil structure to a hairpin structure. This change in structure could be detected by DPI at Hg2+ concentrations smaller than the threshold concentration allowed in drinking water, indicating the sensitivity of this label-free method for Hg2+ detection. High selectivity was indicated when the authors did not observe similar structural changes for Mg2+, Ca2+, Mn2+, Fe3+, Cd2+, Co2+, Ni2+, Zn2+ or Pb2+ ions. A graphical description of this experiment is shown in Figure. Wang et al. later demonstrated that biosensing of small molecules and other metal cations can be achieved using other forms of functionalized DNA that specifically bind the desired analytes. Examples of molecules detected in this manner are shown in Figure \(\PageIndex{18}\).