8.5: Spectroscopic Characterization of Nanoparticles
- Page ID
- 55921
Using UV-vis for the Detection and Characterization of Silicon Quantum Dots
What are Quantum Dots?
Quantum dots (QDs) are small semiconductor nanoparticles generally composed of two elements that have extremely high quantum efficiencies when light is shined on them. The most common quantum dots are CdSe, PbS, and ZnSe, but there are many many other varieties of these particles that contain other elements as well. QDs can also be made of just three elements or just one element such as silicon.
Synthesis of Silicon Quantum Dots
Silicon quantum dots are synthesized in inverse micelles. SiCl4 is reduced using a two fold excess of LiAlH4 (Figure \(\PageIndex{1}\)). After the silicon has been fully reduced and the excess reducing agent quenched, the particles are capped with hydrogens and are hydrophobic. A platinum catalyzed ligand exchange of hydrogen for allylamine will produce hydrophilic particles (Figure \(\PageIndex{2}\)). All reactions in making these particles are extremely air sensitive, and silica is formed readily, so the reactions should be performed in a highly controlled atmosphere, such as a glove box. The particles are then washed in DMF, and finally filtered and stored in deionized water. This will allow the Si QDs to be pure in water, and the particles are ready for analysis. This technique yields Si QDs of 1 - 2 nm in size.
Sample Preparation of Silicon Quantum Dots
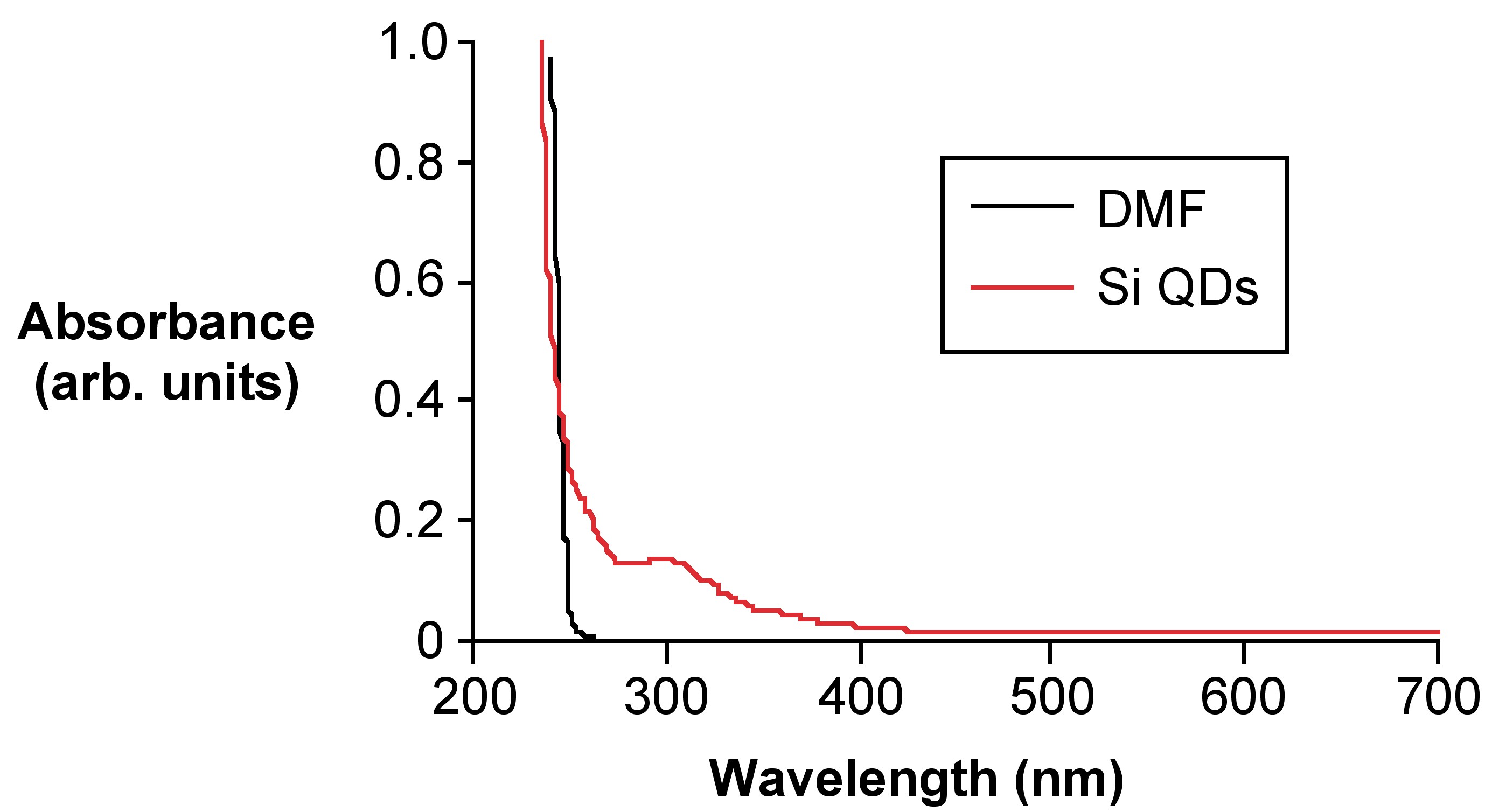
The reported absorbtion wavelength for 1 - 2 nm Si QDs absorb is 300 nm. With the hydrophobic Si QDs, UV-vis absorbance analysis in toluene does not yield an acceptable spectrum because the UV-vis absorbance cutoff is 287 nm, which is very close to 300 nm for the peaks to be resolvable. A better hydrophobic solvent would be hexanes. All measurements of these particles would require a quartz cuvette since the glass aborbance cutoff (300 nm) is exactly where the particles would be observed. Hydrophilic substituted particles do not need to be transferred to another solvent because water’s absorbance cutoff is much lower. There is usually a slight impurity of DMF in the water due to residue on the particles after drying. If there is a DMF peak in the spectrum with the Si QDs the wavelengths are far enough apart to be resolved.
What Information can be Obtained from UV-Visible Spectra?
Quantum dots are especially interesting when it comes to UV-vis spectroscopy because the size of the quantum dot can be determined from the position of the absorbtion peak in the UV-vis spectrum. Quantum dots absorb different wavelengths depending on the size of the particles (e.g., Figure \(\PageIndex{3}\)). Many calibration curves would need to be done to determine the exact size and concentration of the quantum dots, but it is entirely possible and very useful to be able to determine size and concentration of quantum dots in this way since other ways of determining size are much more expensive and extensive (electron microscopy is most widely used for this data).
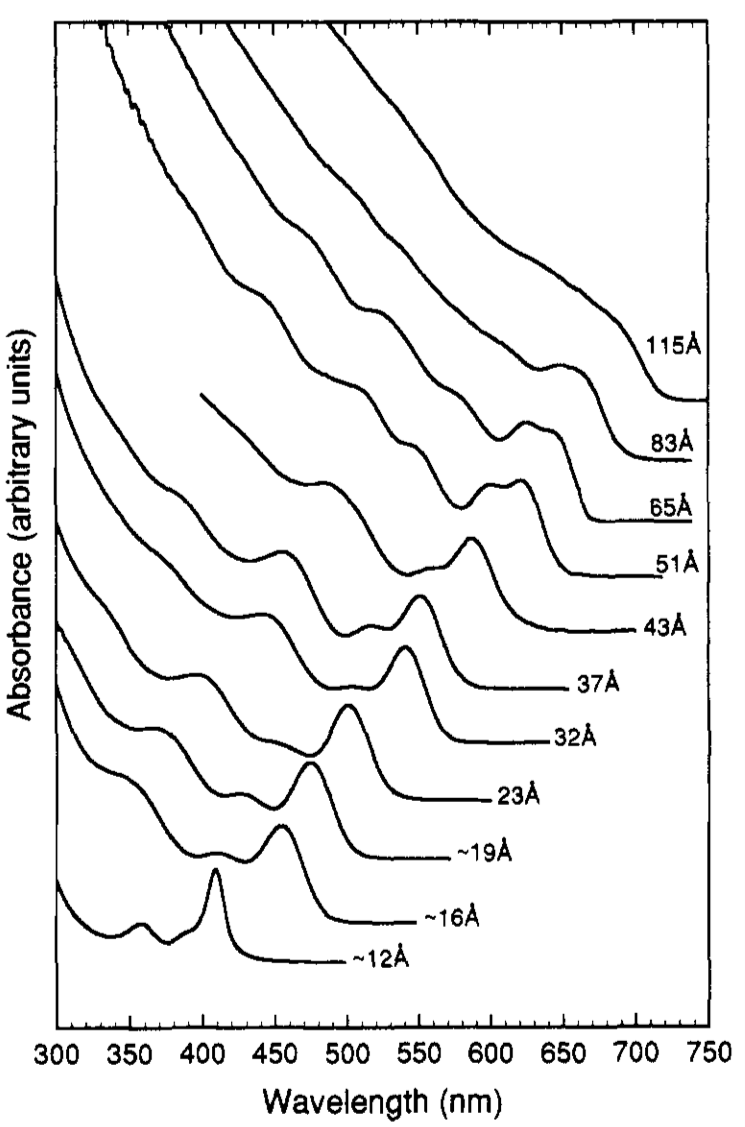
An example of silicon quantum dot data can be seen in Figure \(\PageIndex{4}\). The wider the absorbance peak is, the less monodispersed the sample is.
Why is Knowing the Size of Quantum Dots Important?
Different size (different excitation) quantum dots can be used for different applications. The absorbance of the QDs can also reveal how monodispersed the sample is; more monodispersity in a sample is better and more useful in future applications. Silicon quantum dots in particular are currently being researched for making more efficient solar cells. The monodispersity of these quantum dots is particularly important for getting optimal absorbance of photons from the sun or other light source. Different sized quantum dots will absorb light differently, and a more exact energy absorption is important in the efficiency of solar cells. UV-vis absorbance is a quick, easy, and cheap way to determine the monodispersity of the silicon quantum dot sample. The peak width of the absorbance data can give that information. The other important information for future applications is to get an idea about the size of the quantum dots. Different size QDs absorb at different wavelengths; therefore, specific size Si QDs will be required for different cells in tandem solar cells.
UV-Visible Spectrocopy of Noble Metal Nanoparticles
Noble metal nanoparticles have been used for centuries to color stained glass windows and provide many opportunities for novel sensing and optical technologies due to their intense scattering (deflection) and absorption of light. One of the most interesting and important properties of noble metal nanoparticles is their localized surface plasmon resonance (LSPR). The LSPR of noble metal nanoparticles arises when photons of a certain frequency induce the collective oscillation of conduction electrons on the nanoparticles’ surface. This causes selective photon absorption, efficient scattering, and enhanced electromagnetic field strength around the nanoparticles. More information about the properties and potential applications of noble metal nanoparticles can be found in Silver Nanoparticles: A Case Study in Cutting Edge Research
Synthesis of Noble Metal Nanoparticles
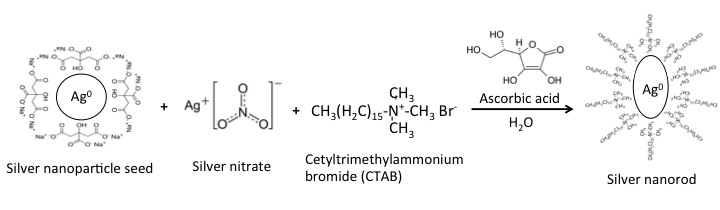
Noble metal nanoparticles can be synthesized via the reduction of metal salts. Spherical metal nanoparticle “seeds” are first synthesized by reducing metal salts in water with a strong reducing agent such as sodium borohydride (Figure \(\PageIndex{5}\)). The seeds are then "capped" to prevent aggregation with a surface group such as citrate (Figure \(\PageIndex{5}\)).

Adjusting the Geometry of Metal Nanoparticles
After small nanoparticle seeds have been synthesized, the seeds can be grown into nanoparticles of various sizes and shapes. Seeds are added to a solution of additional metal salt and a structure-directing agent, and are then reduced with a weak reducing agent such as ascorbic acid (see Figure \(\PageIndex{6}\)). The structure-directing agent will determine the geometry of the nanoparticles produced. For example, cetyltrimethylammonium bromide (CTAB) is often used to produce nanorods (Figure \(\PageIndex{6}\)).
Assemblies of Metal Nanoparticles
Once synthesized, noble metal nanoparticles can be assembled into various higher-order nanostructures. Nanoparticle dimers, linear chains of two nanoparticles, can be assembled using a linker molecule that binds the two nanoparticles together (Figure \(\PageIndex{7}\)). Less-organized nanoparticle assemblies can be formed through the addition of counterions. Counterions react with the surface groups on nanoparticles, causing the nanoparticles to be stripped of their protective surface coating and inducing their aggregation.

UV-Visible Spectroscopy of Noble Metal Nanoparticles
UV-visible absorbance spectroscopy is a powerful tool for detecting noble metal nanoparticles, because the LSPR of metal nanoparticles allows for highly selective absorption of photons. UV-visible absorbance spectroscopy can also be used to detect various factors that affect the LSPR of noble metal nanoparticles. More information about the theory and instrumentation of UV-visible absorbance spectroscopy can be found in the section related to UV-Vis Spectroscopy.
Mie Theory
Mie theory, a theory that describes the interaction of light with a homogenous sphere, can be used to predict the UV-visible absorbance spectrum of spherical metallic nanoparticles. One equation that can be obtained using Mie theory is \ref{1}, which describes the extinction, the sum of absorption and scattering of light, of spherical nanoparticles. In \ref{1}, E(λ) is the extinction, NA is the areal density of the nanoparticles, a is the radius of the nanoparticles, εm is the dielectric constant of the environment surrounding the nanoparticles, λ is the wavelength of the incident light, and εr and εi are the real and imaginary parts of the nanoparticles’ dielectric function. From this relation, we can see that the UV-visible absorbance spectrum of a solution of nanoparticles is dependent on the radius of the nanoparticles, the composition of the nanoparticles, and the environment surrounding the nanoparticles.
\[ E(\lambda )\ = \frac{24\pi N_{A}a^{3}\varepsilon _{m}^{3/2}}{\lambda \ln(10)} \left[\frac{\varepsilon _{i}}{(\varepsilon_{r}\ +\ 2\varepsilon _{m})^{2}\ +\ \varepsilon _{i}^{2}}\right] \label{1} \]
More Advanced Theoretical Techniques
Mie theory is limited to spherical nanoparticles, but there are other theoretical techniques that can be used to predict the UV-visible spectrum of more complex noble metal nanostructures. These techniques include surface-based methods such as the generalized multipole technique and T-matrix method, as well as volume-based techniques such as the discrete dipole approximation and the finite different time domain method.
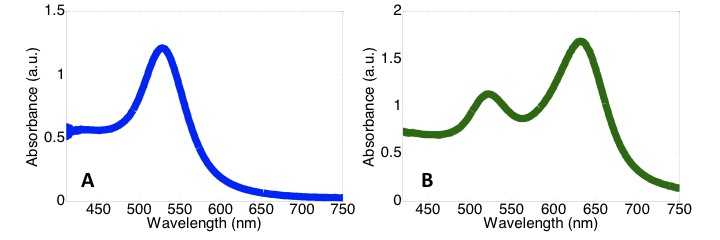
Using UV-Vis Spectroscopy to Predict Nanoparticle Geometry
Just as the theoretical techniques described above can use nanoparticle geometry to predict the UV-visible absorbance spectrum of noble metal nanoparticles, nanoparticles’ UV-visible absorbance spectrum can be used to predict their geometry. As shown in Figure \(\PageIndex{8}\) below, the UV-visible absorbance spectrum is highly dependent on nanoparticle geometry. The shapes of the two spectra are quite different despite the two types of nanoparticles having similar dimensions and being composed of the same material (Figure \(\PageIndex{8}\)).
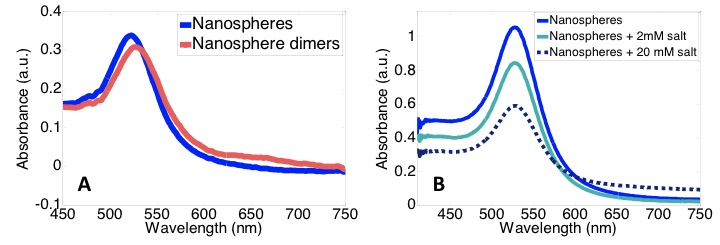
Using UV-Visible Spectroscopy to Determine Nanoparticle Aggregation States
The UV-visible absorbance spectrum is also dependent on the aggregation state of the nanoparticles. When nanoparticles are in close proximity to each other, their plasmons couple, which affects their LSPR and thus their absorption of light. Dimerization of nanospheres causes a “red shift,” a shift to longer wavelengths, in the UV-visible absorbance spectrum as well as a slight increase in absorption at higher wavelengths (see Figure \(\PageIndex{9}\)). Unlike dimerization, aggregation of nanoparticles causes a decrease in the intensity of the peak absorbance without shifting the wavelength at which the peak occurs (λmax). Information about the calculation of λmax can be found in the earlier section about silver nanoparticles. Figure \(\PageIndex{9}\) illustrates the increase in nanoparticle aggregation with increased salt concentrations based on the decreased absorbance peak intensity.
Using UV-Visible Spectroscopy to Determine Nanoparticle Surface Composition
The λmax of the UV-visible absorbance spectrum of noble metal nanoparticles is highly dependent on the environment surrounding the nanoparticles. Because of this, shifts in λmax can be used to detect changes in the surface composition of the nanoparticles. One potential application of this phenomenon is using UV-visible absorbance spectroscopy to detect the binding of biomolecules to the surface of noble metal nanoparticles. The red shift in the λmax of the UV-visible absorbance spectrum in Figure \(\PageIndex{10}\) below with the addition of human serum albumin protein indicates that the protein is binding to the surface of the nanoparticles.

Optical Properties of Group 12-16 (II-VI) Semiconductor Nanoparticles
What are Group 12-16 semiconductors?
Semiconductor materials are generally classified on the basis of the periodic table group that their constituent elements belong to. Thus, Group 12-16 semiconductors, formerly called II-VI semiconductors, are materials whose cations are from the Group 12 and anions are from Group 16 in the periodic table (Figure \(\PageIndex{11}\)). Some examples of Group 12-16 semiconductor materials are cadmium selenide (CdSe), zinc sulfide (ZnS), cadmium teluride (CdTe), zinc oxide (ZnO), and mercuric selenide (HgSe) among others.
The new IUPAC (International Union of Pure and Applied Chemistry) convention is being followed in this document, to avoid any confusion with regard to conventions used earlier. In the old IUPAC convention, Group 12 was known as Group IIB with the roman numeral ‘II’ referring to the number of electrons in the outer electronic shells and B referring to being on the right part of the table. However, in the CAS (Chemical Abstracts Service), the alphabet B refers to transition elements as compared to main group elements, though the roman numeral has the same meaning. Similarly, Group 16 was earlier known as Group VI because all the elements in this group have 6 valence shell electrons.

What are Group 12-16 (II-VI) Semiconductor Nanoparticles?
From the Greek word nanos - meaning "dwarf" this prefix is used in the metric system to mean 10-9 or one billionth (1/1,000,000,000). Thus a nanometer is 10-9 or one billionth of a meter, and a nanojoule is 10-9 or one billionth of a Joule, etc. A nanoparticle is ordinarily defined as any particle with at least one of its dimensions in the 1 - 100 nm range.
Nanoscale materials often show behavior which is intermediate between that of a bulk solid and that of an individual molecule or atom. An inorganic nanocrystal can be imagined to be comprised of a few atoms or molecules. It thus will behave differently from a single atom; however, it is still smaller than a macroscopic solid, and hence will show different properties. For example, if one would compare the chemical reactivity of a bulk solid and a nanoparticle, the latter would have a higher reactivity due to a significant fraction of the total number of atoms being on the surface of the particle. Properties such as boiling point, melting point, optical properties, chemical stability, electronic properties, etc. are all different in a nanoparticle as compared to its bulk counterpart. In the case of Group 12-16 semiconductors, this reduction in size from bulk to the nanoscale results in many size dependent properties such as varying band gap energy, optical and electronic properties.
Optical Properties of Semiconductor Quantum Nanoparticles
In the case of semiconductor nanocrystals, the effect of the size on the optical properties of the particles is very interesting. Consider a Group 12-16 semiconductor, cadmium selenide (CdSe). A 2 nm sized CdSe crystal has a blue color fluorescence whereas a larger nanocrystal of CdSe of about 6 nm has a dark red fluorescence (Figure \(\PageIndex{12}\)). In order to understand the size dependent optical properties of semiconductor nanoparticles, it is important to know the physics behind what is happening at the nano level.

Energy Levels in a Semiconductor
The electronic structure of any material is given by a solution of Schrödinger equations with boundary conditions, depending on the physical situation. The electronic structure of a semiconductor (Figure \(\PageIndex{13}\) can be described by the following terms:
Energy Level
By the solution of Schrödinger’s equations, the electrons in a semiconductor can have only certain allowable energies, which are associated with energy levels. No electrons can exist in between these levels, or in other words can have energies in between the allowed energies. In addition, from Pauli’s Exclusion Principle, only 2 electrons with opposite spin can exist at any one energy level. Thus, the electrons start filling from the lowest energy levels. Greater the number of atoms in a crystal, the difference in allowable energies become very small, thus the distance between energy levels decreases. However, this distance can never be zero. For a bulk semiconductor, due to the large number of atoms, the distance between energy levels is very small and for all practical purpose the energy levels can be described as continuous (Figure \(\PageIndex{13}\)).
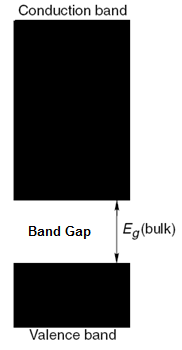
Band Gap
From the solution of Schrödinger’s equations, there are a set of energies which is not allowable, and thus no energy levels can exist in this region. This region is called the band gap and is a quantum mechanical phenomenon (Figure \(\PageIndex{13}\)). In a bulk semiconductor the bandgap is fixed; whereas in a quantum dot nanoparticle the bandgap varies with the size of the nanoparticle.
Conduction Band
The conduction band consists of energy levels from the upper edge of the bandgap and higher (Figure \(\PageIndex{13}\)). To reach the conduction band, the electrons in the valence band should have enough energy to cross the band gap. Once the electrons are excited, they subsequently relax back to the valence band (either radiatively or non-radiatively) followed by a subsequent emission of radiation. This property is responsible for most of the applications of quantum dots.
Exciton and Exciton Bohr Radius
When an electron is excited from the valence band to the conduction band, corresponding to the electron in the conduction band a hole (absence of electron) is formed in the valence band. This electron pair is called an exciton. Excitons have a natural separation distance between the electron and hole, which is characteristic of the material. This average distance is called exciton Bohr radius. In a bulk semiconductor, the size of the crystal is much larger than the exciton Bohr radius and hence the exciton is free to move throughout the crystal.
Energy Levels in a Quantum Dot Semiconductor
Before understanding the electronic structure of a quantum dot semiconductor, it is important to understand what a quantum dot nanoparticle is. We earlier studied that a nanoparticle is any particle with one of its dimensions in the 1 - 100 nm. A quantum dot is a nanoparticle with its diameter on the order of the materials exciton Bohr radius. Quantum dots are typically 2 - 10 nm wide and approximately consist of 10 to 50 atoms. With this understanding of a quantum dot semiconductor, the electronic structure of a quantum dot semiconductor can be described by the following terms.
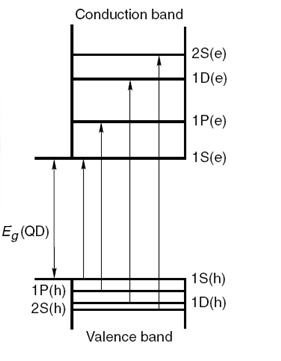
Quantum Confinement
When the size of the semiconductor crystal becomes comparable or smaller than the exciton Bohr radius, the quantum dots are in a state of quantum confinement. As a result of quantum confinement, the energy levels in a quantum dot are discrete (Figure \(\PageIndex{14}\) as opposed to being continuous in a bulk crystal (Figure \(\PageIndex{13}\)).
Discrete Energy Levels
In materials that have small number of atoms and are considered as quantum confined, the energy levels are separated by an appreciable amount of energy such that they are not continuous, but are discrete (see Figure \(\PageIndex{13}\)). The energy associated with an electron (equivalent to conduction band energy level) is given by is given by \ref{2}, where h is the Planck’s constant, me is the effective mass of electron and n is the quantum number for the conduction band states, and n can take the values 1, 2, 3 and so on. Similarly, the energy associated with the hole (equivalent to valence band energy level) is given by \ref{2}, where n' is the quantum number for the valence states, and n' can take the values 1, 2, 3, and so on. The energy increases as one goes higher in the quantum number. Since the electron mass is much smaller than that of the hole, the electron levels are separated more widely than the hole levels.
\[ E^{e}\ =\ \frac{h^{2}n^{2}}{8\pi ^{2}m_e d^2 } \label{2} \]
\[E^h \ =\ \frac{h^{2}n'^{2}}{8\pi ^{2}m_h d^2 } \label{3} \]
Tunable Band Gap
As seen from \ref{2} and \ref{3}, the energy levels are affected by the diameter of the semiconductor particles. If the diameter is very small, since the energy is dependent on inverse of diameter squared, the energy levels of the upper edge of the band gap (lowest conduction band level) and lower edge of the band gap (highest valence band level) change significantly with the diameter of the particle and the effective mass of the electron and the hole, resulting in a size dependent tunable band gap. This also results in the discretization of the energy levels.
Qualitatively, this can be understood in the following way. In a bulk semiconductor, the addition or removal of an atom is insignificant compared to the size of the bulk semiconductor, which consists of a large number of atoms. The large size of bulk semiconductors makes the changes in band gap so negligible on the addition of an atom, that it is considered as a fixed band gap. In a quantum dot, addition of an atom does make a difference, resulting in the tunability of band gap.
UV-Visible Absorbance
Due to the presence of discrete energy levels in a QD, there is a widening of the energy gap between the highest occupied electronic states and the lowest unoccupied states as compared to the bulk material. As a consequence, the optical properties of the semiconductor nanoparticles also become size dependent.
The minimum energy required to create an exciton is the defined by the band gap of the material, i.e., the energy required to excite an electron from the highest level of valence energy states to the lowest level of the conduction energy states. For a quantum dot, the bandgap varies with the size of the particle. From \ref{2} and \ref{3}, it can be inferred that the band gap becomes higher as the particle becomes smaller. This means that for a smaller particle, the energy required for an electron to get excited is higher. The relation between energy and wavelength is given by \ref{4}, where h is the Planck’s constant, c is the speed of light, λ is the wavelength of light. Therefore, from \ref{4} to cross a bandgap of greater energy, shorter wavelengths are absorbed, i.e., a blue shift is seen.
\[ E\ =\ hc \label{4} \]
For Group 12-16 semiconductors, the bandgap energy falls in the UV-visible range. That is ultraviolet light or visible light can be used to excite an electron from the ground valence states to the excited conduction states. In a bulk semiconductor the band gap is fixed, and the energy states are continuous. This results in a rather uniform absorption spectrum (Figure \(\PageIndex{15}\) a).
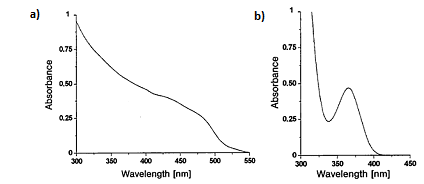
In the case of Group 12-16 quantum dots, since the bandgap can be changed with the size, these materials can absorb over a range of wavelengths. The peaks seen in the absorption spectrum (Figure \(\PageIndex{15}\) b) orrespond to the optical transitions between the electron and hole levels. The minimum energy and thus the maximum wavelength peak corresponds to the first exciton peak or the energy for an electron to get excited from the highest valence state to the lowest conduction state. The quantum dot will not absorb wavelengths of energy longer than this wavelength. This is known as the absorption onset.
Fluorescence
Fluorescence is the emission of electromagnetic radiation in the form of light by a material that has absorbed a photon. When a semiconductor quantum dot (QD) absorbs a photon/energy equal to or greater than its band gap, the electrons in the QD’s get excited to the conduction state. This excited state is however not stable. The electron can relax back to its ground state by either emitting a photon or lose energy via heat losses. These processes can be divided into two categories – radiative decay and non-radiative decay. Radiative decay is the loss of energy through the emission of a photon or radiation. Non-radiative decay involves the loss of heat through lattice vibrations and this usually occurs when the energy difference between the levels is small. Non-radiative decay occurs much faster than radiative decay.
Usually the electron relaxes to the ground state through a combination of both radiative and non-radiative decays. The electron moves quickly through the conduction energy levels through small non-radiative decays and the final transition across the band gap is via a radiative decay. Large nonradiative decays don’t occur across the band gap because the crystal structure can’t withstand large vibrations without breaking the bonds of the crystal. Since some of the energy is lost through the non-radiative decay, the energy of the emitted photon, through the radiative decay, is much lesser than the absorbed energy. As a result the wavelength of the emitted photon or fluorescence is longer than the wavelength of absorbed light. This energy difference is called the Stokes shift. Due this Stokes shift, the emission peak corresponding to the absorption band edge peak is shifted towards a higher wavelength (lower energy), i.e., Figure \(\PageIndex{16}\).
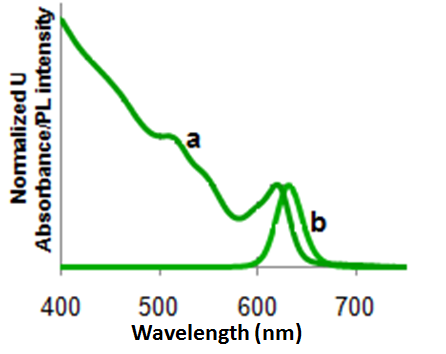
Intensity of emission versus wavelength is a bell-shaped Gaussian curve. As long as the excitation wavelength is shorter than the absorption onset, the maximum emission wavelength is independent of the excitation wavelength. Figure \(\PageIndex{16}\) shows a combined absorption and emission spectrum for a typical CdSe tetrapod.
Factors Affecting the Optical Properties of NPs
There are various factors that affect the absorption and emission spectra for Group 12-16 semiconductor quantum crystals. Fluorescence is much more sensitive to the background, environment, presence of traps and the surface of the QDs than UV-visible absorption. Some of the major factors influencing the optical properties of quantum nanoparticles include:
- Surface defects, imperfection of lattice, surface charges- The surface defects and imperfections in the lattice structure of semiconductor quantum dots occur in the form of unsatisfied valencies. Similar to surface charges, unsatisfied valencies provide a sink for the charge carriers, resulting in unwanted recombinations.
- Surface ligands- The presence of surface ligands is another factor that affects the optical properties. If the surface ligand coverage is a 100%, there is a smaller chance of surface recombinations to occur.
- Solvent polarity- The polarity of solvents is very important for the optical properties of the nanoparticles. If the quantum dots are prepared in organic solvent and have an organic surface ligand, the more non-polar the solvent, the particles are more dispersed. This reduces the loss of electrons through recombinations again, since when particles come in close proximity to each other, increases the non-radiative decay events.
Applications of the Optical Properties of Group 12-16 Semiconductor NPs
The size dependent optical properties of NP’s have many applications from biomedical applications to solar cell technology, from photocatalysis to chemical sensing. Most of these applications use the following unique properties.
For applications in the field of nanoelectronics, the sizes of the quantum dots can be tuned to be comparable to the scattering lengths, reducing the scattering rate and hence, the signal to noise ratio. For Group 12-16 QDs to be used in the field of solar cells, the bandgap of the particles can be tuned so as to form absorb energy over a large range of the solar spectrum, resulting in more number of excitons and hence more electricity. Since the nanoparticles are so small, most of the atoms are on the surface. Thus, the surface to volume ratio is very large for the quantum dots. In addition to a high surface to volume ratio, the Group 12-16 QDs respond to light energy. Thus quantum dots have very good photocatalytic properties. Quantum dots show fluorescence properties, and emit visible light when excited. This property can be used for applications as biomarkers. These quantum dots can be tagged to drugs to monitor the path of the drugs. Specially shaped Group 12-16 nanoparticles such as hollow shells can be used as drug delivery agents. Another use for the fluorescence properties of Group 12-16 semiconductor QDs is in color-changing paints, which can change colors according to the light source used.
Characterization of Group 12-16 (II-VI) Semiconductor Nanoparticles by UV-Visible Spectroscopy
Quantum dots (QDs) as a general term refer to nanocrystals of semiconductor materials, in which the size of the particles are comparable to the natural characteristic separation of an electron-hole pair, otherwise known as the exciton Bohr radius of the material. When the size of the semiconductor nanocrystal becomes this small, the electronic structure of the crystal is governed by the laws of quantum physics. Very small Group 12-16 (II-VI) semiconductor nanoparticle quantum dots, in the order of 2 - 10 nm, exhibit significantly different optical and electronic properties from their bulk counterparts. The characterization of size dependent optical properties of Group 12-16 semiconductor particles provide a lot of qualitative and quantitative information about them – size, quantum yield, monodispersity, shape and presence of surface defects. A combination of information from both the UV-visible absorption and fluorescence, complete the analysis of the optical properties.
UV-Visible Absorbance Spectroscopy
Absorption spectroscopy, in general, refers to characterization techniques that measure the absorption of radiation by a material, as a function of the wavelength. Depending on the source of light used, absorption spectroscopy can be broadly divided into infrared and UV-visible spectroscopy. The band gap of Group 12-16 semiconductors is in the UV-visible region. This means the minimum energy required to excite an electron from the valence states of the Group 12-16 semiconductor QDs to its conduction states, lies in the UV-visible region. This is also a reason why most of the Group 12-16 semiconductor quantum dot solutions are colored.
This technique is complementary to fluorescence spectroscopy, in that UV-visible spectroscopy measures electronic transitions from the ground state to the excited state, whereas fluorescence deals with the transitions from the excited state to the ground state. In order to characterize the optical properties of a quantum dot, it is important to characterize the sample with both these techniques
In quantum dots, due to the very small number of atoms, the addition or removal of one atom to the molecule changes the electronic structure of the quantum dot dramatically. Taking advantage of this property in Group 12-16 semiconductor quantum dots, it is possible to change the band gap of the material by just changing the size of the quantum dot. A quantum dot can absorb energy in the form of light over a range of wavelengths, to excite an electron from the ground state to its excited state. The minimum energy that is required to excite an electron, is dependent on the band gap of the quantum dot. Thus, by making accurate measurements of light absorption at different wavelengths in the ultraviolet and visible spectrum, a correlation can be made between the band gap and size of the quantum dot. Group 12-16 semiconductor quantum dots are of particular interest, since their band gap lies in the visible region of the solar spectrum.
The UV-visible absorbance spectroscopy is a characterization technique in which the absorbance of the material is studied as a function of wavelength. The visible region of the spectrum is in the wavelength range of 380 nm (violet) to 740 nm (red) and the near ultraviolet region extends to wavelengths of about 200 nm. The UV-visible spectrophotometer analyzes over the wavelength range 200 – 900 nm.
When the Group 12-16 semiconductor nanocrystals are exposed to light having an energy that matches a possible electronic transition as dictated by laws of quantum physics, the light is absorbed and an exciton pair is formed. The UV-visible spectrophotometer records the wavelength at which the absorption occurs along with the intensity of the absorption at each wavelength. This is recorded in a graph of absorbance of the nanocrystal versus wavelength.
Instrumentation
A working schematic of the UV-visible spectrophotometer is show in Figure \(\PageIndex{17}\).

The Light Source
Since it is a UV-vis spectrophotometer, the light source (Figure \(\PageIndex{17}\)) needs to cover the entire visible and the near ultra-violet region (200 - 900 nm). Since it is not possible to get this range of wavelengths from a single lamp, a combination of a deuterium lamp for the UV region of the spectrum and tungsten or halogen lamp for the visible region is used. This output is then sent through a diffraction grating as shown in the schematic.
The Diffraction Grating and the Slit
The beam of light from the visible and/or UV light source is then separated into its component wavelengths (like a very efficient prism) by a diffraction grating (Figure \(\PageIndex{17}\)). Following the slit is a slit that sends a monochromatic beam into the next section of the spectrophotometer.
Rotating Discs
Light from the slit then falls onto a rotating disc (Figure \(\PageIndex{17}\)). Each disc consists of different segments – an opaque black section, a transparent section and a mirrored section. If the light hits the transparent section, it will go straight through the sample cell, get reflected by a mirror, hits the mirrored section of a second rotating disc, and then collected by the detector. Else if the light hits the mirrored section, gets reflected by a mirror, passes through the reference cell, hits the transparent section of a second rotating disc and then collected by the detector. Finally if the light hits the black opaque section, it is blocked and no light passes through the instrument, thus enabling the system to make corrections for any current generated by the detector in the absence of light.
Sample Cell, Reference Cell and Sample Preparation
For liquid samples, a square cross section tube sealed at one end is used. The choice of cuvette depends on the following factors:
- Type of solvent - For aqueous samples, specially designed rectangular quartz, glass or plastic cuvettes are used. For organic samples glass and quartz cuvettes are used.
- Excitation wavelength – Depending on the size and thus, bandgap of the 12-16 semiconductor nanoparticles, different excitation wavelengths of light are used. Depending on the excitation wavelength, different materials are used
| Cuvette | Wavelength (nm) |
|---|---|
| Visible only glass | 380-780 |
| Visible only plastic | 380-780 |
| UV plastic | 220-780 |
| Quartz | 200-900 |
- Cost - Plastic cuvettes are the least expensive and can be discarded after use. Though quartz cuvettes have the maximum utility, they are the most expensive, and need to reused. Generally, disposable plastic cuvettes are used when speed is more important than high accuracy.
The best cuvettes need to be very clear and have no impurities that might affect the spectroscopic reading. Defects on the cuvette such as scratches, can scatter light and hence should be avoided. Some cuvettes are clear only on two sides, and can be used in the UV-Visible spectrophotometer, but cannot be used for fluorescence spectroscopy measurements. For Group 12-16 semiconductor nanoparticles prepared in organic solvents, the quartz cuvette is chosen.
In the sample cell the quantum dots are dispersed in a solvent, whereas in the reference cell the pure solvent is taken. It is important that the sample be very dilute (maximum first exciton absorbance should not exceed 1 au) and the solvent is not UV-visible active. For these measurements, it is required that the solvent does not have characteristic absorption or emission in the region of interest. Solution phase experiments are preferred, though it is possible to measure the spectra in the solid state also using thin films, powders, etc. The instrumentation for solid state UV-visible absorption spectroscopy is slightly different from the solution phase experiments and is beyond the scope of discussion.
Detector
Detector converts the light into a current signal that is read by a computer. Higher the current signal, greater is the intensity of the light. The computer then calculates the absorbance using the in \ref{5}, here A denotes absorbance, I is sample cell intensity and Io is the reference cell intensity.
\[ A\ =\ log_{10}(I_{0}/I) \label{5} \]
The following cases are possible:
Where I < I0 and A < 0. This usually occurs when the solvent absorbs in the wavelength range. Preferably the solvent should be changed, to get an accurate reading for actual reference cell intensity.
Where I = I0 and A= 0. This occurs when pure solvent is put in both reference and sample cells. This test should always be done before testing the sample, to check for the cleanliness of the cuvettes.
When A = 1. This occurs when 90% or the light at a particular wavelength has been absorbed, which means that only 10% is seen at the detector. So I0/I becomes 100/10 = 10. Log10 of 10 is 1.
When A > 1. This occurs in extreme case where more than 90% of the light is absorbed.
Output
The output is the form of a plot of absorbance against wavelength, e.g., Figure \(\PageIndex{18}\).
Beer-Lambert Law
In order to make comparisons between different samples, it is important that all the factors affecting absorbance should be constant except the sample itself.
Effect of Concentration on Absorbance
The extent of absorption depends on the number of absorbing nanoparticles or in other words the concentration of the sample. If it is a reasonably concentrated solution, it will have a high absorbance since there are lots of nanoparticles to interact with the light. Similarly in an extremely dilute solution, the absorbance is very low. In order to compare two solutions, it is important that we should make some allowance for the concentration.
Effect of Container Shape
Even if we had the same concentration of solutions, if we compare two solutions – one in a rectagular shaped container (e.g., Figure \(\PageIndex{19}\)) so that light travelled 1 cm through it and the other in which the light travelled 100 cm through it, the absorbance would be different. This is because if the length the light travelled is greater, it means that the light interacted with more number of nanocrystals, and thus has a higher absorbance. Again, in order to compare two solutions, it is important that we should make some allowance for the concentration.
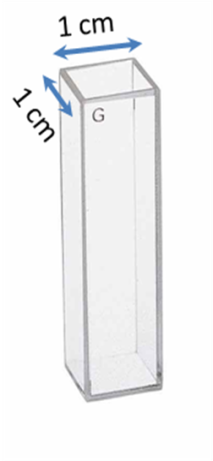
The Law
The Beer-Lambert law addresses the effect of concentration and container shape as shown in \ref{5}, \ref{6} and \ref{7}, where A denotes absorbance; ε is the molar absorptivity or molar absorption coefficient; l is the path length of light (in cm); and c is the concentration of the solution (mol/dm3).
\[ log_{10}(I_{0}/I)\ =\ \varepsilon l c \label{6} \]
\[ A\ =\ \varepsilon l c \label{7} \]
Molar Absorptivity
From the Beer-Lambert law, the molar absorptivity 'ε' can be expressed as shown in \ref{8}.
\[ c\ =\ A/l \varepsilon \label{8} \]
Molar absorptivity corrects for the variation in concentration and length of the solution that the light passes through. It is the value of absorbance when light passes through 1 cm of a 1 mol/dm3 solution.
Limitations of Beer-Lambert Law
The linearity of the Beer-Lambert law is limited by chemical and instrumental factors.
- At high concentrations (> 0.01 M), the relation between absorptivity coefficient and absorbance is no longer linear. This is due to the electrostatic interactions between the quantum dots in close proximity.
- If the concentration of the solution is high, another effect that is seen is the scattering of light from the large number of quantum dots.
- The spectrophotometer performs calculations assuming that the refractive index of the solvent does not change significantly with the presence of the quantum dots. This assumption only works at low concentrations of the analyte (quantum dots).
- Presence of stray light.
Analysis of Data
The data obtained from the spectrophotometer is a plot of absorbance as a function of wavelength. Quantitative and qualitative data can be obtained by analysing this information.
Quantitative Information
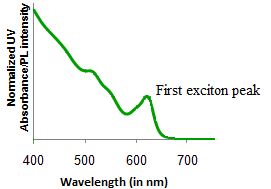
The band gap of the semiconductor quantum dots can be tuned with the size of the particles. The minimum energy for an electron to get excited from the ground state is the energy to cross the band gap. In an absorption spectra, this is given by the first exciton peak at the maximum wavelength (λmax).
Size of the Quantum Dots
The size of quantum dots can be approximated corresponding to the first exciton peak wavelength. Emperical relationships have been determined relating the diameter of the quantum dot to the wavelength of the first exciton peak. The Group 12-16 semiconductor quantum dots that they studied were cadmium selenide (CdSe), cadmium telluride (CdTe) and cadmium sulfide (CdS). The empirical relationships are determined by fitting experimental data of absorbance versus wavelength of known sizes of particles. The empirical equations determined are given for CdTe, CdSe, and CdS in \ref{9}, \ref{10} and \ref{11} respectively, where D is the diameter and λ is the wavelength corresponding to the first exciton peak. For example, if the first exciton peak of a CdSe quantum dot is 500 nm, the corresponding diameter of the quantum dot is 2.345 nm and for a wavelength of 609 nm, the corresponding diameter is 5.008 nm.
\[ D\ =\ (9.8127\ x\ 10^{-7})\lambda ^{3}\ -\ (1.7147\ x\ 10^{-3})\lambda ^{2}\ +\ (1.0064)\lambda \ -\ 194.84 \label{9} \]
\[ D\ =\ (1.6122\ x\ 10^{-7})\lambda ^{3}\ -\ (2.6575\ x\ 10^{-3})\lambda ^{2}\ +\ (1.6242)\lambda \ -\ 41.57 \label{10} \]
\[ D\ =\ (-6.6521\ x\ 10^{-7})\lambda ^{3}\ -\ (1.9577\ x\ 10^{-3})\lambda ^{2}\ +\ (9.2352)\lambda \ -\ 13.29 \label{11} \]
Concentration of Sample
Using the Beer-Lambert law, it is possible to calculate the concentration of the sample if the molar absorptivity for the sample is known. The molar absorptivity can be calculated by recording the absorbance of a standard solution of 1 mol/dm3 concentration in a standard cuvette where the light travels a constant distance of 1 cm. Once the molar absorptivity and the absorbance of the sample are known, with the length the light travels being fixed, it is possible to determine the concentration of the sample solution.
Empirical equations can be determined by fitting experimental data of extinction coefficient per mole of Group 12-16 semiconductor quantum dots, at 250 °C, to the diameter of the quantum dot, \ref{12}, \ref{13}, and \ref{14}.
\[ \varepsilon \ =\ 10043 x D^{2.12} \label{12} \]
\[ \varepsilon \ =\ 5857\ x\ D^{2.65} \label{13} \]
\[ \varepsilon \ =\ 21536\ x\ D^{2.3} \label{14} \]
The concentration of the quantum dots can then be then be determined by using the Beer Lambert law as given by \ref{8}.
Qualitative Information
Apart from quantitative data such as the size of the quantum dots and concentration of the quantum dots, a lot of qualitative information can be derived from the absorption spectra.
Size Distribution
If there is a very narrow size distribution, the first exciton peak will be very sharp (Figure \(\PageIndex{20}\)). his is because due to the narrow size distribution, the differences in band gap between different sized particles will be very small and hence most of the electrons will get excited over a smaller range of wavelengths. In addition, if there is a narrow size distribution, the higher exciton peaks are also seen clearly.
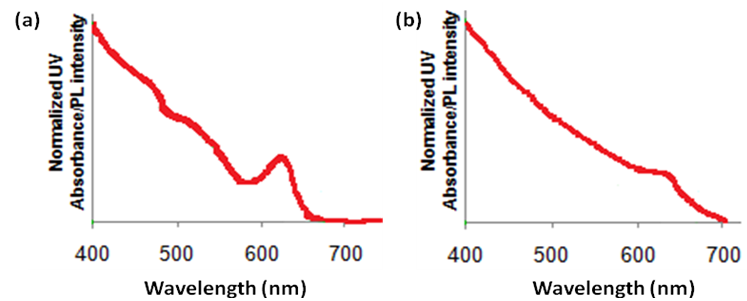
Shapd Particles
In the case of a spherical quantum dot, in all dimensions, the particle is quantum confined (Figure \(\PageIndex{21}\)). In the case of a nanorod, whose length is not in the quantum regime, the quantum effects are determined by the width of the nanorod. Similar is the case in tetrapods or four legged structures. The quantum effects are determined by the thickness of the arms. During the synthesis of the shaped particles, the thickness of the rod or the arm of the tetrapod does not vary among the different particles, as much as the length of the rods or arms changes. Since the thickness of the rod or tetrapod is responsible for the quantum effects, the absorption spectrum of rods and tetrapods has sharper features as compared to a quantum dot. Hence, qualitatively it is possible to differentiate between quantum dots and other shaped particles.
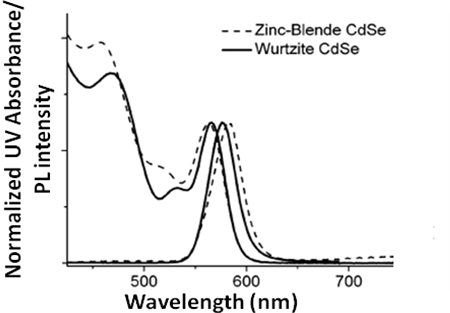
Crystal Lattice Information
In the case of CdSe semiconductor quantum dots it has been shown that it is possible to estimate the crystal lattice of the quantum dot from the adsorption spectrum (Figure \(\PageIndex{22}\)), and hence determine if the structure is zinc blend or wurtzite.
UV-Vis Absorption Spectra of Group 12-16 Semiconductor Nanoparticles
Cadmium Selenide (CdSe)
Cadmium selenide (CdSe) is one of the most popular Group 12-16 semiconductors. This is mainly because the band gap (712 nm or 1.74 eV) energy of CdSe. Thus, the nanoparticles of CdSe can be engineered to have a range of band gaps throughout the visible range, corresponding to the major part of the energy that comes from the solar spectrum. This property of CdSe along with its fluorescing properties is used in a variety of applications such as solar cells and light emitting diodes. Though cadmium and selenium are known carcinogens, the harmful biological effects of CdSe can be overcome by coating the CdSe with a layer of zinc sulfide. Thus CdSe, can also be used as bio-markers, drug-delivery agents, paints and other applications.
A typical absorption spectrum of narrow size distribution wurtzite CdSe quantum dot is shown in Figure \(\PageIndex{23}\). A size evolving absorption spectra is shown in Figure \(\PageIndex{24}\). However, a complete analysis of the sample is possible only by also studying the fluorescence properties of CdSe.
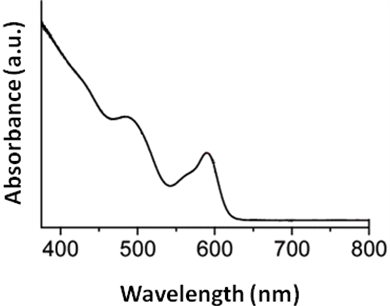
Cadmium Telluride (CdTe)
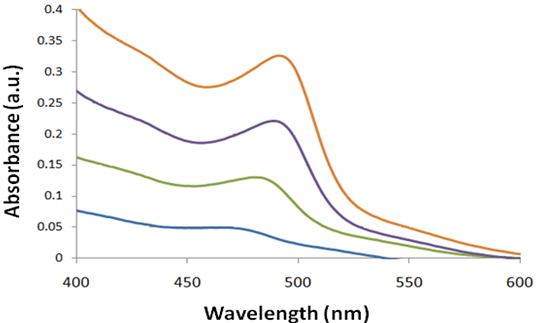
Cadmium telluride has a band gap of 1.44 eV (860 nm) and as such it absorbs in the infrared region. Like CdSe, the sizes of CdTe can be engineered to have different band edges and thus, different absorption spectra as a function of wavelength. A typical CdTe spectra is shown in Figure \(\PageIndex{25}\). Due to the small bandgap energy of CdTe, it can be used in tandem with CdSe to absorb in a greater part of the solar spectrum.
Other Group 12-16 Semiconductor Systems
Table \(\PageIndex{1}\) shows the bulk band gap of other Group 12-16 semiconductor systems. The band gap of ZnS falls in the UV region, while those of ZnSe, CdS, and ZnTe fall in the visible region.
| Material | Band Gap (eV) | Wavelength (nm) |
| ZnS | 3.61 | 343.2 |
| ZnSe | 2.69 | 460.5 |
| ZnTe | 2.39 | 518.4 |
| CdS | 2.49 | 497.5 |
| CdSe | 1.74 | 712.1 |
| CsTe | 1.44 | 860.3 |
Heterostructures of Group 12-16 Semiconductor Systems
It is often desirable to have a combination of two Group 12-16 semiconductor system quantum heterostructures of different shapes like dots and tetrapods, for applications in solar cells, bio-markers, etc. Some of the most interesting systems are ZnS shell-CdSe core systems, such as the CdSe/CdS rods and tetrapods.
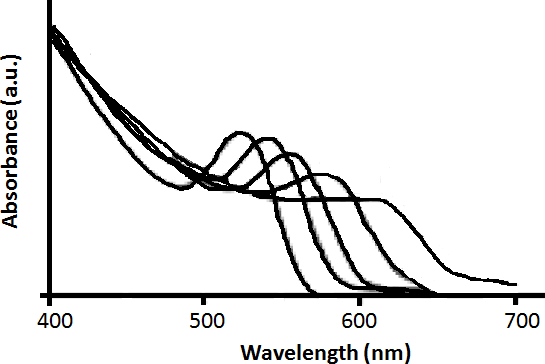
Figure \(\PageIndex{26}\) shows a typical absorption spectra of CdSe-ZnS core-shell system. This system is important because of the drastically improved fluorescence properties because of the addition of a wide band gap ZnS shell than the core CdSe. In addition with a ZnS shell, CdSe becomes bio-compatible.
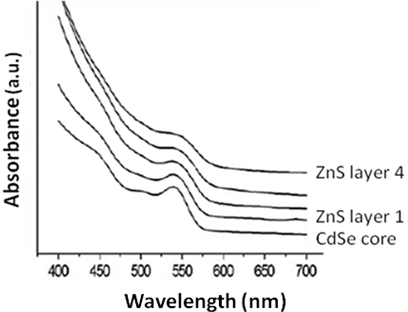
A CdSe seed, CdS arm nanorods system is also interesting. Combining CdSe and CdS in a single nanostructure creates a material with a mixed dimensionality where holes are confined to CdSe while electrons can move freely between CdSe and CdS phases.
Optical Characterization of Group 12-16 (II-VI) Semiconductor Nanoparticles by Fluorescence Spectroscopy
Group 12-16 semiconductor nanocrystals when exposed to light of a particular energy absorb light to excite electrons from the ground state to the excited state, resulting in the formation of an electron-hole pair (also known as excitons). The excited electrons relax back to the ground state, mainly through radiative emission of energy in the form of photons.
Quantum dots (QD) refer to nanocrystals of semiconductor materials where the size of the particles is comparable to the natural characteristic separation of an electron-hole pair, otherwise known as the exciton Bohr radius of the material. In quantum dots, the phenomenon of emission of photons associated with the transition of electrons from the excited state to the ground state is called fluorescence.
Fluorescence Spectroscopy
Emission spectroscopy, in general, refers to a characterization technique that measures the emission of radiation by a material that has been excited. Fluorescence spectroscopy is one type of emission spectroscopy which records the intensity of light radiated from the material as a function of wavelength. It is a nondestructive characterization technique.
After an electron is excited from the ground state, it needs to relax back to the ground state. This relaxation or loss of energy to return to the ground state, can be achieved by a combination of non-radiative decay (loss of energy through heat) and radiative decay (loss of energy through light). Non-radiative decay by vibrational modes typically occurs between energy levels that are close to each other. Radiative decay by the emission of light occurs when the energy levels are far apart like in the case of the band gap. This is because loss of energy through vibrational modes across the band gap can result in breaking the bonds of the crystal. This phenomenon is shown in Figure \(\PageIndex{27}\).
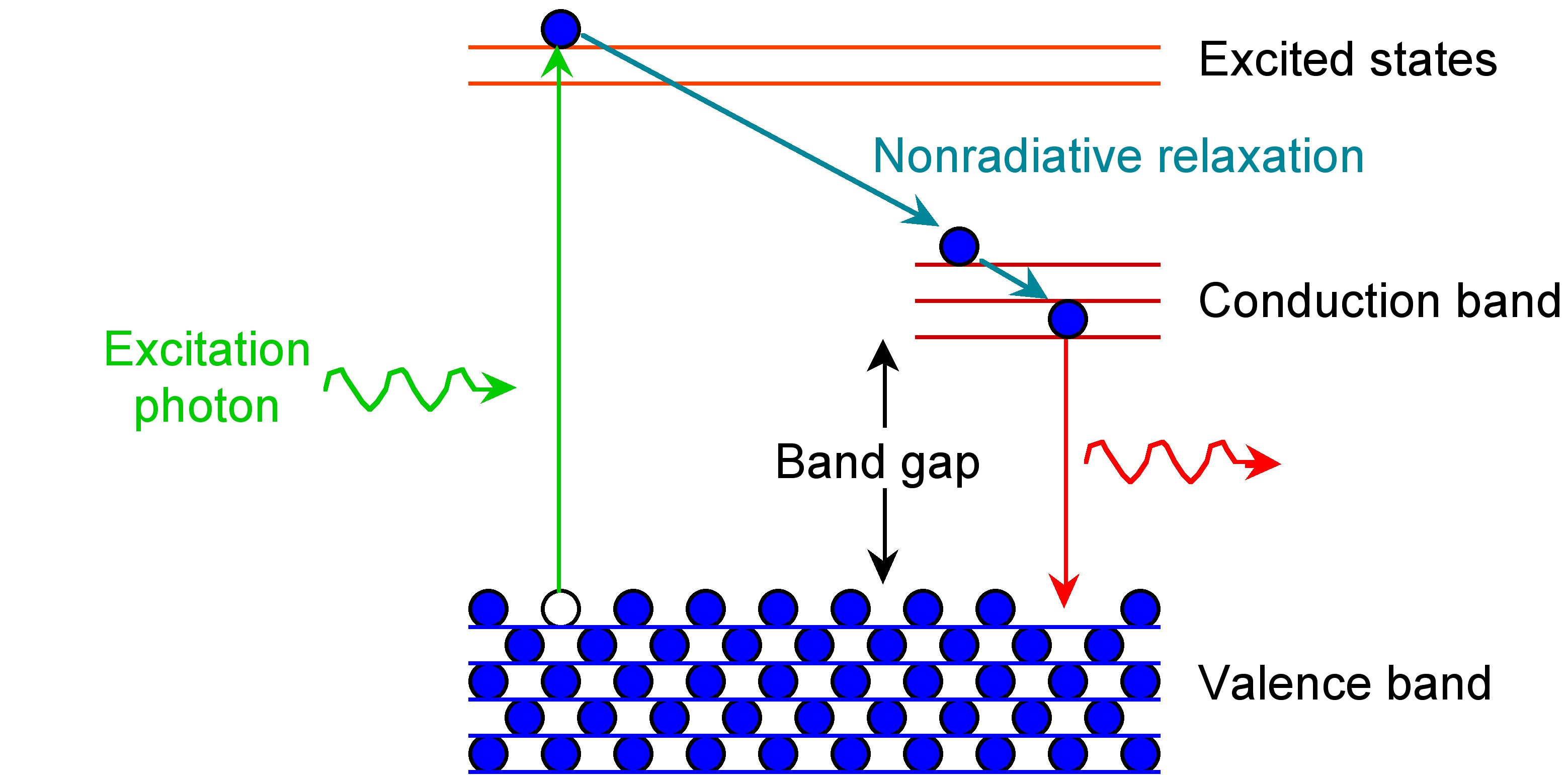
The band gap of Group 12-16 semiconductors is in the UV-visible region. Thus, the wavelength of the emitted light as a result of radiative decay is also in the visible region, resulting in fascinating fluorescence properties.
A fluorimeter is a device that records the fluorescence intensity as a function of wavelength. The fluorescence quantum yield can then be calculated by the ratio of photons absorbed to photons emitted by the system. The quantum yield gives the probability of the excited state getting relaxed via fluorescence rather than by any other non-radiative decay.
Difference between Fluorescence and Phosphorescence
Photoluminescence is the emission of light from any material due to the loss of energy from excited state to ground state. There are two main types of luminescence – fluorescence and phosphorescence. Fluorescence is a fast decay process, where the emission rate is around 108 s-1 and the lifetime is around 10-9 - 10-7 s. Fluorescence occurs when the excited state electron has an opposite spin compared to the ground state electrons. From the laws of quantum mechanics, this is an allowed transition, and occurs rapidly by emission of a photon. Fluorescence disappears as soon as the exciting light source is removed.
Phosphorescence is the emission of light, in which the excited state electron has the same spin orientation as the ground state electron. This transition is a forbidden one and hence the emission rates are slow (103 - 100 s-1). So the phosphorescence lifetimes are longer, typically seconds to several minutes, while the excited phosphors slowly returned to the ground state. Phosphorescence is still seen, even after the exciting light source is removed. Group 12-16 semiconductor quantum dots exhibit fluorescence properties when excited with ultraviolet light.
Instrumentation
The working schematic for the fluorometer is shown in Figure \(\PageIndex{28}\).
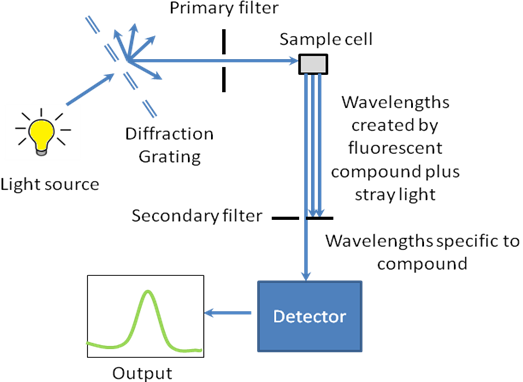
The Light Source
The excitation energy is provided by a light source that can emit wavelengths of light over the ultraviolet and the visible range. Different light sources can be used as excitation sources such as lasers, xenon arcs and mercury-vapor lamps. The choice of the light source depends on the sample. A laser source emits light of a high irradiance at a very narrow wavelength interval. This makes the need for the filter unnecessary, but the wavelength of the laser cannot be altered significantly. The mercury vapor lamp is a discrete line source. The xenon arc has a continuous emission spectrum between the ranges of 300 - 800 nm.
The Diffraction Grating and Primary Filter
The diffraction grating splits the incoming light source into its component wavelengths (Figure \(\PageIndex{29}\)). The monochromator can then be adjusted to choose with wavelengths to pass through. Following the primary filter, specific wavelengths of light are irradiated onto the sample.
Sample Cell and Sample Preparation
A proportion of the light from the primary filter is absorbed by the sample. After the sample gets excited, the fluorescent substance returns to the ground state, by emitting a longer wavelength of light in all directions (Figure \(\PageIndex{28}\)). Some of this light passes through a secondary filter. For liquid samples, a square cross section tube sealed at one end and all four sides clear, is used as a sample cell. The choice of cuvette depends on three factors:
1. Type of Solvent - For aqueous samples, specially designed rectangular quartz, glass or plastic cuvettes are used. For organic samples glass and quartz cuvettes are used.
2. Excitation Wavelength - Depending on the size and thus, bandgap of the Group 12-16 semiconductor nanoparticles, different excitation wavelengths of light are used. Depending on the excitation wavelength, different materials are used (Table \(\PageIndex{2}\)).
| Cuvette | Wavelength (nm) |
| Visible only glass | 380-780 |
| Visible only plastic | 380-780 |
| UV plastic | 220-780 |
| Quartz | 200-900 |
3. Cost - Plastic cuvettes are the least expensive and can be discarded after use. Though quartz cuvettes have the maximum utility, they are the most expensive, and need to reused. Generally, disposable plastic cuvettes are used when speed is more important than high accuracy.
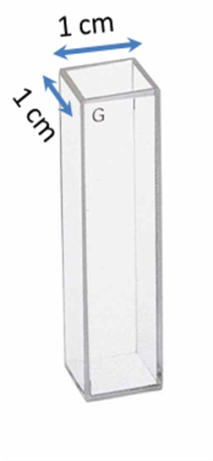
The cuvettes have a 1 cm path length for the light (Figure \(\PageIndex{29}\)). The best cuvettes need to be very clear and have no impurities that might affect the spectroscopic reading. Defects on the cuvette, such as scratches, can scatter light and hence should be avoided. Since the specifications of a cuvette are the same for both, the UV-visible spectrophotometer and fluorimeter, the same cuvette that is used to measure absorbance can be used to measure the fluorescence. For Group 12-16 semiconductor nanoparticles preparted in organic solvents, the clear four sided quartz cuvette is used. The sample solution should be dilute (absorbance <1 au), to avoid very high signal from the sample to burn out the detector. The solvent used to disperse the nanoparticles should not absorb at the excitation wavelength.
Secondary Filter
The secondary filter is placed at a 90° angle (Figure \(\PageIndex{28}\)) to the original light path to minimize the risk of transmitted or reflected incident light reaching the detector. Also this minimizes the amount of stray light, and results in a better signal-to-noise ratio. From the secondary filter, wavelengths specific to the sample are passed onto the detector.
Detector
The detector can either be single-channeled or multichanneled (Figure \(\PageIndex{28}\)). The single-channeled detector can only detect the intensity of one wavelength at a time, while the multichanneled detects the intensity at all wavelengths simultaneously, making the emission monochromator or filter unnecessary. The different types of detectors have both advantages and disadvantages.
Output
The output is the form of a plot of intensity of emitted light as a function of wavelength as shown in Figure \(\PageIndex{30}\)).
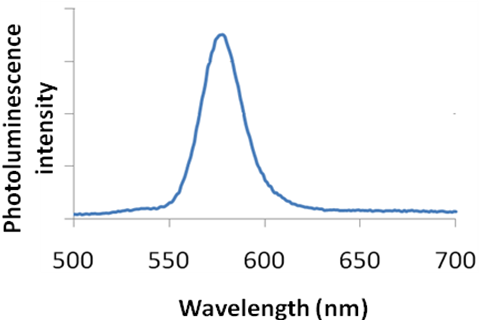
Analysis of Data
The data obtained from fluorimeter is a plot of fluorescence intensity as a function of wavelength. Quantitative and qualitative data can be obtained by analysing this information.
Quantitative Information
From the fluorescence intensity versus wavelength data, the quantum yield (ΦF) of the sample can be determined. Quantum yield is a measure of the ratio of the photons absorbed with respect to the photons emitted. It is important for the application of Group 12-16 semiconductor quantum dots using their fluorescence properties, for e.g., bio-markers.
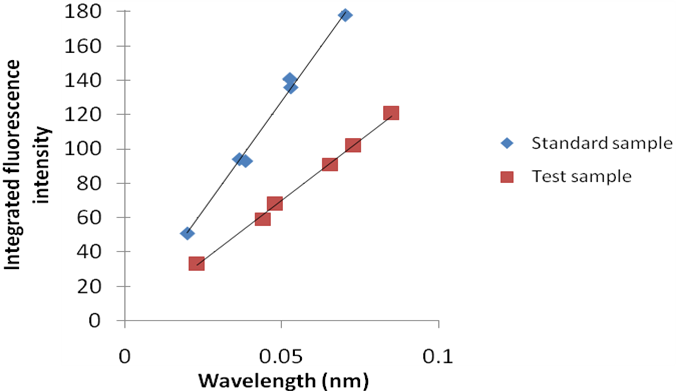
The most well-known method for recording quantum yield is the comparative method which involves the use of well characterized standard solutions. If a test sample and a standard sample have similar absorbance values at the same excitation wavelength, it can be assumed that the number of photons being absorbed by both the samples is the same. This means that a ratio of the integrated fluorescence intensities of the test and standard sample measured at the same excitation wavelength will give a ratio of quantum yields. Since the quantum yield of the standard solution is known, the quantum yield for the unknown sample can be calculated.
A plot of integrated fluorescence intensity versus absorbance at the excitation wavelength is shown in Figure \(\PageIndex{31}\). The slope of the graphs shown in Figure \(\PageIndex{31}\) are proportional to the quantum yield of the different examples. Quantum yield is then calculated using \ref{15}, where subscripts ST denotes standard sample and X denotes the test sample; QY is the quantum yield; RI is the refractive index of the solvent.
\[ \frac{QY_{X}}{QY_{ST}}\ =\ \frac{slope_{X} (RI_{X})^{2}}{slope_{ST} (RI_{ST})^{2}} \label{15} \]
Take the example of Figure \(\PageIndex{32}\). If the same solvent is used in both the sample and the standard solution, the ratio of quantum yields of the sample to the standard is given by \ref{16}. If the quantum yield of the standard is known to 0.95, then the quantum yield of the test sample is 0.523 or 52.3%.
\[ \frac{QY_{X}}{QY_{ST}}\ =\ \frac{1.41}{2.56} \label{16} \]
The assumption used in the comparative method is valid only in the Beer-Lambert law linear regime. Beer-Lambert law states that absorbance is directly proportional to the path length of light travelled within the sample, and concentration of the sample. The factors that affect the quantum yield measurements are the following:
- Concentration - Low concentrations should be used (absorbance < 0.2 a.u.) to avoid effects such as self quenching.
- Solvent - It is important to take into account the solvents used for the test and standard solutions. If the solvents used for both are the same then the comparison is trivial. However, if the solvents in the test and standard solutions are different, this difference needs to be accounted for. This is done by incorporating the solvent refractive indices in the ratio calculation.
- Standard Samples - The standard samples should be characterized thoroughly. In addition, the standard sample used should absorb at the excitation wavelength of the test sample.
- Sample Preparation - It is important that the cuvettes used are clean, scratch free and clear on all four sides. The solvents used must be of spectroscopic grade and should not absorb in the wavelength range.
- Slit Width - The slit widths for all measurements must be kept constant.
The quantum yield of the Group 12-16 semiconductor nanoparticles are affected by many factors such as the following.
- Surface Defects - The surface defects of semiconductor quantum dots occur in the form of unsatisfied valencies. Thus resulting in unwanted recombinations. These unwanted recombinations reduce the loss of energy through radiative decay, and thus reducing the fluorescence.
- Surface Ligands - If the surface ligand coverage is a 100%, there is a smaller chance of surface recombinations to occur.
- Solvent Polarity - If the solvent and the ligand have similar solvent polarities, the nanoparticles are more dispersed, reducing the loss of electrons through recombinations.
Qualitative Information
Apart from quantum yield information, the relationship between intensity of fluorescence emission and wavelength, other useful qualitative information such as size distribution, shape of the particle and presence of surface defects can be obtained.
As shown in Figure \(\PageIndex{32}\), the shape of the plot of intensity versus wavelength is a Gaussian distribution. In Figure \(\PageIndex{32}\), the full width at half maximum (FWHM) is given by the difference between the two extreme values of the wavelength at which the photoluminescence intensity is equal to half its maximum value. From the full width half max (FWHM) of the fluorescence intensity Gaussian distribution, it is possible to determine qualitatively the size distribution of the sample. For a Group 12-16 quantum dot sample if the FWHM is greater than 30, the system is very polydisperse and has a large size distribution. It is desirable for all practical applications for the FWHM to be lesser than 30.
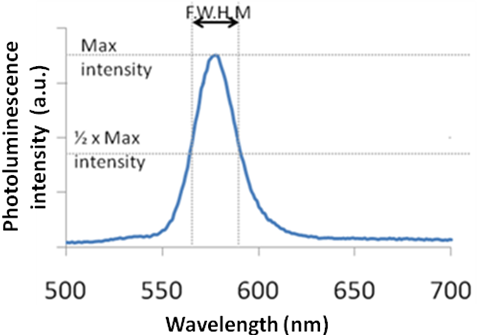
From the FWHM of the emission spectra, it is also possible to qualitatively get an idea if the particles are spherical or shaped. During the synthesis of the shaped particles, the thickness of the rod or the arm of the tetrapod does not vary among the different particles, as much as the length of the rods or arms changes. The thickness of the arm or rod is responsible for the quantum effects in shaped particles. In the case of quantum dots, the particle is quantum confined in all dimensions. Thus, any size distribution during the synthesis of quantum dots greatly affects the emission spectra. As a result the FWHM of rods and tetrapods is much smaller as compared to a quantum dot. Hence, qualitatively it is possible to differentiate between quantum dots and other shaped particles.
Another indication of branched structures is the decrease in the intensity of fluorescence peaks. Quantum dots have very high fluorescence values as compared to branched particles, since they are quantum confined in all dimensions as compared to just 1 or 2 dimensions in the case of branched particles.
Fluorescence Spectra of Different Group 12-16 Semiconductor Nanoparticles
The emission spectra of all Group 12-16 semiconductor nanoparticles are Gaussian curves as shown in Figure \(\PageIndex{30}\) and Figure \(\PageIndex{32}\). The only difference between them is the band gap energy, and hence each of the Group 12-16 semiconductor nanoparticles fluoresce over different ranges of wavelengths.
Cadmium Selenide
Since its bulk band gap (1.74 eV, 712 nm) falls in the visible region cadmium Selenide (CdSe) is used in various applications such as solar cells, light emitting diodes, etc. Size evolving emission spectra of cadmium selenide is shown in Figure \(\PageIndex{33}\). Different sized CdSe particles have different colored fluorescence spectra. Since cadmium and selenide are known carcinogens and being nanoparticles are easily absorbed into the human body, there is some concern regarding these particles. However, CdSe coated with ZnS can overcome all the harmful biological effects, making cadmium selenide nanoparticles one of the most popular 12-16 semiconductor nanoparticle.
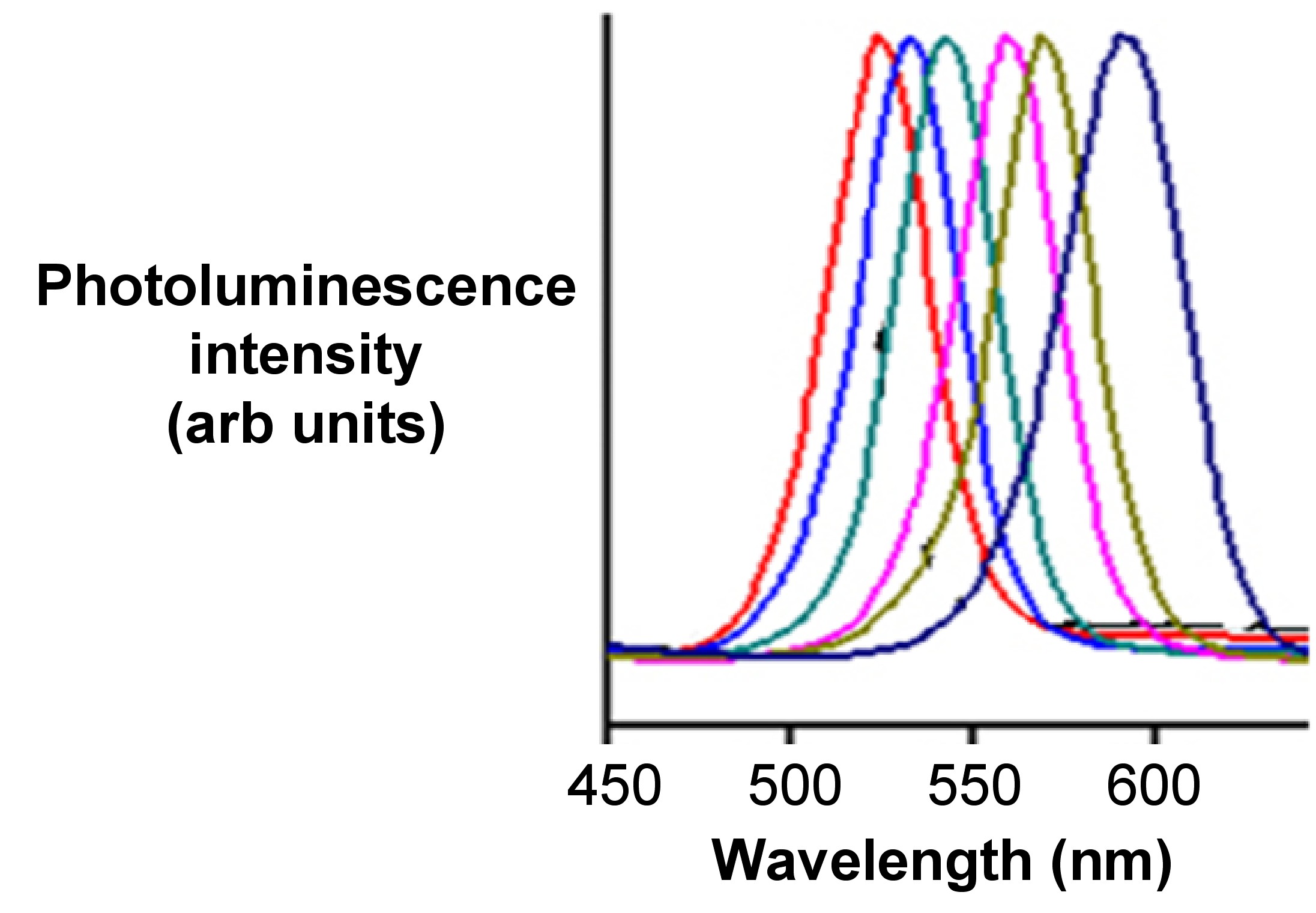
A combination of the absorbance and emission spectra is shown in Figure \(\PageIndex{34}\) for four different sized particles emitting green, yellow, orange, and red fluorescence.
Cadmium Telluride
Cadmium Telluride (CdTe) has a band gap of 1.44 eV and thus absorbs in the infra red region. The size evolving CdTe emission spectra is shown in Figure \(\PageIndex{35}\).
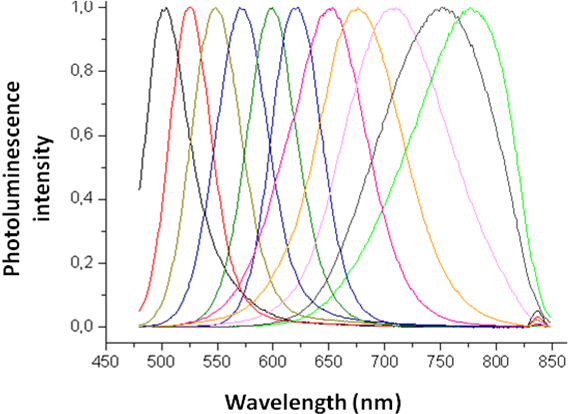
Adding Shells to QDs
Capping a core quantum dot with a semiconductor material with a wider bandgap than the core, reduces the nonradiative recombination and results in brighter fluorescence emission. Quantum yields are affected by the presences of free surface charges, surface defects and crystal defects, which results in unwanted recombinations. The addition of a shell reduces the nonradiative transitions and majority of the electrons relax radiatively to the valence band. In addition, the shell also overcomes some of the surface defects.
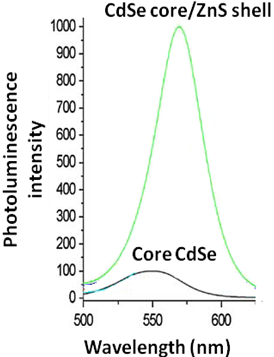
For the CdSe-core/ZnS-shell systems exhibit much higher quantum yield as compared to core CdSe quantum dots as seen in Figure \(\PageIndex{36}\).
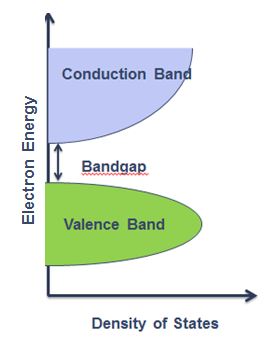
Band Gap Measurement
In solid state physics a band gap also called an energy gap, is an energy range in an ideal solid where no electron states can exist. As shown in Figure \(\PageIndex{37}\) for an insulator or semiconductor the band gap generally refers to the energy difference between the top of the valence band and the bottom of the conduction band. This is equivalent to the energy required to free an outer shell electron from its orbit about the nucleus to become a mobile charge carrier, able to move freely within the solid material.
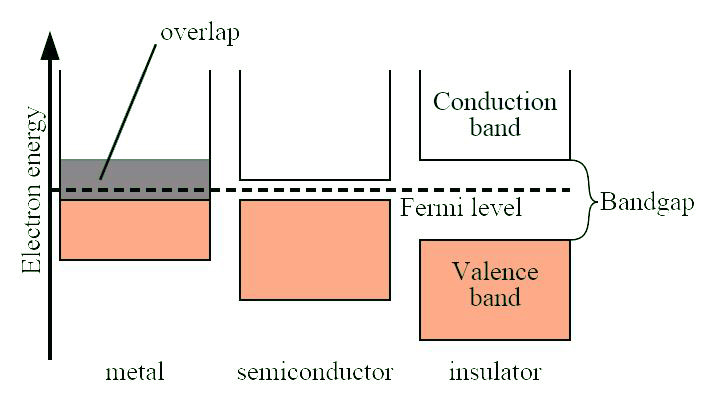
The band gap is a major factor determining the electrical conductivity of a solid. Substances with large band gaps are generally insulators (i.e., dielectric), those with smaller band gaps are semiconductors, while conductors either have very small band gaps or no band gap (because the valence and conduction bands overlap as shown in Figure \(\PageIndex{38}\).
The theory of bands in solids is one of the most important steps in the comprehension of the properties of solid matter. The existence of a forbidden energy gap in semiconductors is an essential concept in order to be able to explain the physics of semiconductor devices. For example, the magnitude of the bad gap of solid determines the frequency or wavelength of the light, which will be adsorbed. Such a value is useful for photocatalysts and for the performance of a dye sensitized solar cell.
Nanocomposites materials are of interest to researchers the world over for various reasons. One driver for such research is the potential application in next-generation electronic and photonic devices. Particles of a nanometer size exhibit unique properties such as quantum effects, short interface migration distances (and times) for photoinduced holes and electrons in photochemical and photocatalytic systems, and increased sensitivity in thin film sensors.
Measurement Methods
Electrical measurement method
For a p-n junction, the essential electrical characteristic is that it constitutes a rectifier, which allows the easy flow of a charge in one direction but restrains the flow in the opposite direction. The voltage-current characteristic of such a device can be described by the Shockley equation, \ref{17}, in which, I0 is the reverse bias saturation current, q the charge of the electron, k is Boltzmann’s constant, and T is the temperature in Kelvin.
\[ I\ =\ I_{0}(e^{qV/kT} - 1) \label{17} \]
When the reverse bias is very large, the current I is saturated and equal to I0. This saturation current is the sum of several different contributions. They are diffusion current, generation current inside the depletion zone, surface leakage effects and tunneling of carriers between states in the band gap. In a first approximation at a certain condition, I0 can be interpreted as being solely due to minority carriers accelerated by the depletion zone field plus the applied potential difference. Therefore it can be shown that, \ref{18}, where A is a constant, Eg the energy gap (slightly temperature dependent), and γ an integer depending on the temperature dependence of the carrier mobility µ.
\[ I_{0}\ =\ AT^{(3\ +\ \gamma /2)}e^{-E_{g}(T)/KT} \label{18} \]
We can show that γ is defined by the relation by a more advanced treatment, \ref{19}.
\[ T \mu^{2} \ =\ T^{\gamma } \label{19} \]
After substituting the value of I0 given by \ref{17} into \ref{18}, we take the napierian logarithm of the two sides and multiply them by kT for large forward bias (qV > 3kT); thus, rearranging, we have \ref{20}.
\[ qV\ =\ E_{g}(T)\ +\ T[k\ ln(1/A)]\ -\ (3+\gamma /2)klnT \label{20} \]
As InT can be considered as a slowly varying function in the 200 - 400 K interval, therefore for a constant current, I, flowing through the junction a plot of qV versus the temperature should approximate a straight line, and the intercept of this line with the qV axis is the required value of the band gap Eg extrapolated to 0 K. Through \ref{21} instead of qV, we can get a more precise value of Eg.
\[ qV_{c}\ =\ qV\ +\ (3+\gamma /2)klnT \label{21} \]
\ref{20} shows that the value of γ depends on the temperature and µ that is a very complex function of the particular materials, doping and processing. In the 200 - 400 K range, one can estimate that the variation ΔEg produced by a change of Δγ in the value of γ is \ref{22}. So a rough value of γ is sufficient for evaluating the correction. By taking the experimental data for the temperature dependence of the mobility µ, a mean value for γ can be found. Then the band gap energy qV can be determined.
\[ \Delta E_{g}\ =\ 10^{-2}eV\Delta \gamma \label{22} \]
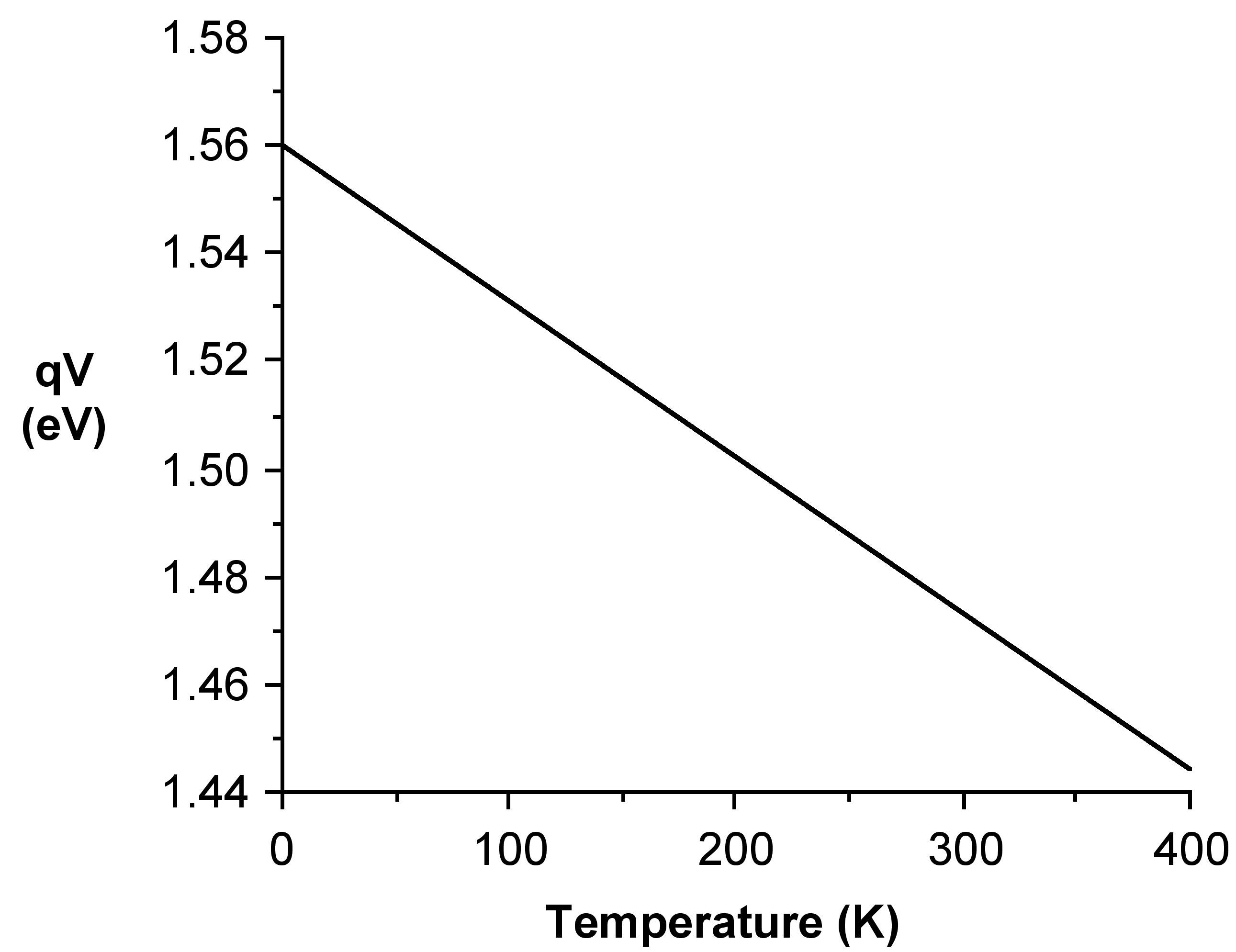
The electrical circuit required for the measurement is very simple and the constant current can be provided by a voltage regulator mounted as a constant current source (see Figure \(\PageIndex{39}\)). The potential difference across the junction can be measured with a voltmeter. Five temperature baths were used: around 90 °C with hot water, room temperature water, water-ice mixture, ice-salt-water mixture and mixture of dry ice and acetone. The result for GaAs is shown in Figure \(\PageIndex{40}\). The plot qV corrected (qVc) versus temperature gives E1 = 1.56±0.02 eV for GaAs. This may be compared with literature value of 1.53 eV.
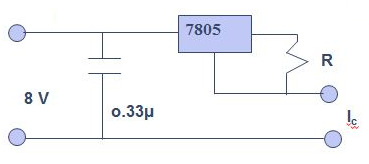
Optical Measurement Method
Optical method can be described by using the measurement of a specific example, e.g., hexagonal boron nitride (h-BN, Figure \(\PageIndex{41}\). The UV-visible absorption spectrum was carried out for investigating the optical energy gap of the h-BN film based on its optically induced transition.
For this study, a sample of h-BN was first transferred onto an optical quartz plate, and a blank quartz plate was used for the background as the reference substrate. The following Tauc’s equation was used to determine the optical band gap Eg, \ref{23}, where ε is the optical absorbance, λ is the wavelength and ω = 2π/λ is the angular frequency of the incident radiation.
\[ \omega ^{2} \varepsilon \ =\ (h\omega \ -\ E_{g})^{2} \label{23} \]
As Figure \(\PageIndex{42}\)a shows, the absorption spectrum has one sharp absorption peak at 201 - 204 nm. On the basis of Tauc’s formulation, it is speculated that the plot of ε1/2/λ versus 1/λ should be a straight line at the absorption range. Therefore, the intersection point with the x axis is 1/λg (λg is defined as the gap wavelength). The optical band gap can be calculated based on Eg) hc/λg. The plot in Figure \(\PageIndex{42}\)b shows ε1/2/λ versus 1/λ curve acquired from the thin h-BN film. For more than 10 layers sample, he calculated gap wavelength λg is about 223 nm, which corresponds to an optical band gap of 5.56 eV.
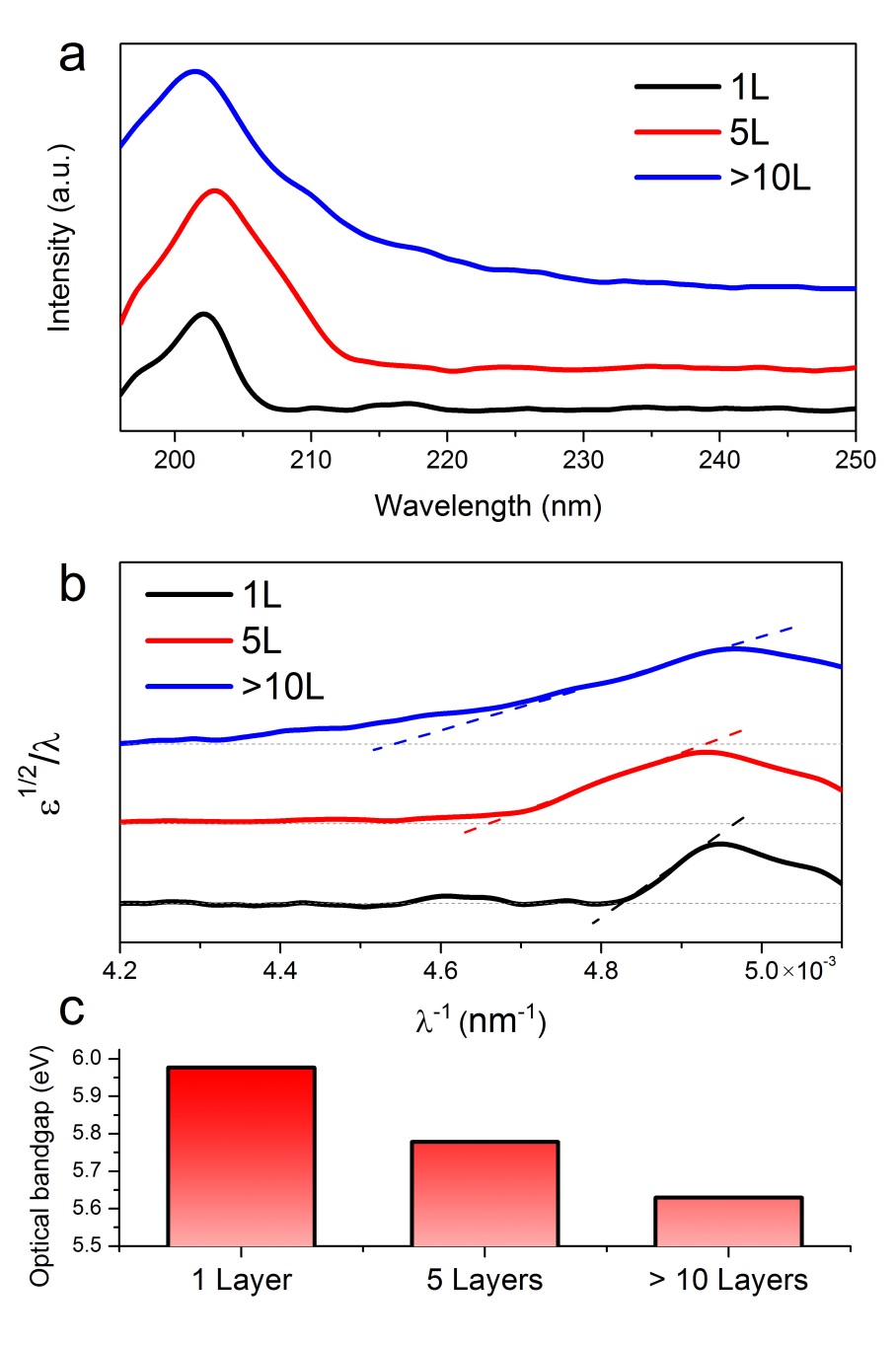
Previous theoretical calculations of a single layer of h-BN shows 6 eV band gap as the result. The thickness of h-BN film are 1 layer, 5 layers and thick (>10 layers) h-BN films, the measured gap is about 6.0, 5.8, 5.6 eV, respectively, which is consistent with the theoretical gap value. For thicker samples, the layer-layer interaction increases the dispersion of the electronic bands and tends to reduce the gap. From this example, we can see that the band gap is relative to the size of the materials, this is the most important feature of nano material.
Band Gap Measurements of Quantum Dots
A semiconductor is a material that has unique properties in the way it reacts to electrical current. A semiconductor’s ability to conduct an electrical current is intermediate between that of an insulator (such as rubber or glass) and a conductor (such as copper). However, the conductivity of a semiconductor material increases with increasing temperature, a behavior opposite to that of a metal. Semiconductors may also have a lower resistance to the flow of current in one direction than in the other.
Band Theory
The properties of semiconductors can best be understood by band theory, where the difference between conductors, semiconductors, and insulators can be understood by increasing separations between a valence band and a conduction band, as shown in Figure \(\PageIndex{43}\). In semiconductors a small energy gap separates the valence band and the conduction band. This energy gap is smaller than that of insulators – which is too large for essentially any electrons from the valence band to enter the conduction band – and larger than that of conductors, where the valence and conduction bands overlap. At 0 K all of the electrons in a semiconductor lie in the valence band, but at higher temperatures some electrons will have enough energy to be promoted to the conduction band

Carrier Generation and Recombination
In addition to the band structure of solids, the concept of carrier generation and recombination is very important to the understanding of semiconducting materials. Carrier generation and recombination is the process by which mobile charge carriers (electrons and electron holes) are created and eliminated. The valence band in semiconductors is normally very full and its electrons immobile, resulting in no flow as electrical current. However, if an electron in the valence band acquires enough energy to reach the conduction band, it can flow freely in the nearly empty conduction band. Furthermore, it will leave behind an electron hole that can flow as current exactly like a physical charged particle. The energy of an electron-electron hole pair is quantified in the form of a neutrally-charged quasiparticle called an exciton. For semiconducting materials, there is a characteristic separation distance between the electron and the hole in an exciton called the exciton Bohr radius. The exciton Bohr radius has large implications for the properties of quantum dots.
The process by which electrons gain energy and move from the valence to the conduction band is termed carrier generation, while recombination describes the process by which electrons lose energy and re-occupy the energy state of an electron hole in the valence band. Carrier generation is accompanied by the absorption of radiation, while recombination is accompanied by the emission of radiation.
Quantum Dots
In the 1980s, a new nanoscale (~1-10 nm) semiconducting structure was developed that exhibits properties intermediate between bulk semiconductors and discrete molecules. These semiconducting nanocrystals, called quantum dots, are small enough to be subjected to quantum effects, which gives them interesting properties and the potential to be useful in a wide-variety of applications. The most important characteristic of quantum dots (QDs) is that they are highly tunable, meaning that the optoelectronic properties are dependent on the particles size and shape. As Figure \(\PageIndex{44}\) illustrates, the band gap in a QD is inversely related to its size, which produces a blue shift in emitted light as the particle size decreases. The highly tunable nature of QDs result not only from the inverse relationship between band gap size and particle size, but also from the ability to set the size of QDs and make QDs out of a wide variety of materials. The potential to produce QDs with properties tailored to fulfill a specific function has produce an enormous amount of interest in quantum dots (see the section on Optical Properties of Group 12-16 (II-VI) Semiconductor Nanoparticles).

Band Gap Measurements of QDs
As previously mentioned, QDs are small enough that quantum effects influence their properties. At sizes under approximately 10 nm, quantum confinement effects dominate the optoelectronic properties of a material. Quantum confinement results from electrons and electron holes being squeezed into a dimension that approaches a critical quantum measurement, called the exciton Bohr radius. As explained above, the distance between the electron and the hole within an exciton is called the exciton Bohr radius. In bulk semiconductors the exciton can move freely in all directions, but when the size of a semiconductor is reduced to only a few nanometers, quantum confinement effects occur and the band gap properties are changed. Confinement of the exciton in one dimension produces a quantum well, confinement in two dimensions produces a quantum wire, and confinement in all three dimensions produces a quantum dot.
Recombination occurs when an electron from a higher energy level relaxes to a lower energy level and recombines with an electron hole. This process is accompanied by the emission of radiation, which can be measured to give the band gap size of a semiconductor. The energy of the emitted photon in a recombination process of a QD can be modeled as the sum of the band gap energy, the confinement energies of the excited electron and the electron hole, and the bound energy of the exciton as show in \ref{24}.
\[ E\ =\ E_{bandgap}\ +\ E_{confinement}\ +\ E_{exciton} \label{24} \]
The confinement energy can be modeled as a simple particle in a one-dimensional box problem and the energy levels of the exciton can be represented as the solutions to the equation at the ground level (n = 1) with the mass replaced by the reduced mass. The confinement energy is given by \ref{25}, where ħ is the reduced Plank’s constant, µ is the reduced mass, and a is the particle radius. me and mh are the effective masses of the electron and the hole, respectively.
\[ E_{confinement}\ =\ \frac{\hbar ^{2} \pi ^{2}}{2a^{2}}(\frac{1}{m_{e}}+\frac{1}{m_{h}})=\ \frac{\hbar ^{2}\pi ^{2}}{2\mu a^{2}} \label{25} \]
The bound exciton energy can be modeled by using the Coulomb interaction between the electron and the positively charged electron-hole, as shown in \ref{26}. The negative energy is proportional to Rydberg’s energy (Ry) (13.6 eV) and inversely proportional to the square of the size-dependent dielectric constant, εr. µ and me are the reduced mass and the effective mass of the electron, respectively.
\[ E\ =\ -R_{y} \frac{1}{\varepsilon _{r}^{2}}\frac{\mu }{m_{e}} +\ -R_{y}^{*} \label{26} \]
Using these models and spectroscopic measurements of the emitted photon energy (E), it is possible to measure the band gap of QDs.
Photoluminescence Spectroscopy
Photoluminescence (PL) Spectroscopy is perhaps the best way to measure the band gap of QDs. PL spectroscopy is a contactless, nondestructive method that is extremely useful in measuring the separation between different energy levels. PL spectroscopy works by directing light onto a sample, where energy is absorbed by electrons in the sample and elevated to a higher energy-state through a process known as photo-excitation. Photo-excitation produces the electron-electron hole pair. The recombination of the electron-electron hole pair then occurs with the emission of radiation (light). The energy of the emitted light (photoluminescence) relates to the difference in energy levels between the lower (ground) electronic state and the higher (excited) electronic state. This amount of energy is measured by PL spectroscopy to give the band gap size.
PL spectroscopy can be divided in two different categories: fluorescence and phosphorescence. It is fluorescent PL spectroscopy that is most relevant to QDs. In fluorescent PL spectroscopy, an electron is raised from the ground state to some elevated excited state. The electron than relaxes (loses energy) to the lowest electronic excited state via a non-radiative process. This non-radiative relaxation can occur by a variety of mechanisms, but QDs typically dissipate this energy via vibrational relaxation. This form of relaxation causes vibrations in the material, which effectively heat the QD without emitting light. The electron then decays from the lowest excited state to the ground state with the emission of light. This means that the energy of light absorbed is greater than the energy of the light emitted. The process of fluorescence is schematically summarized in the Jablonski diagram in Figure \(\PageIndex{45}\).
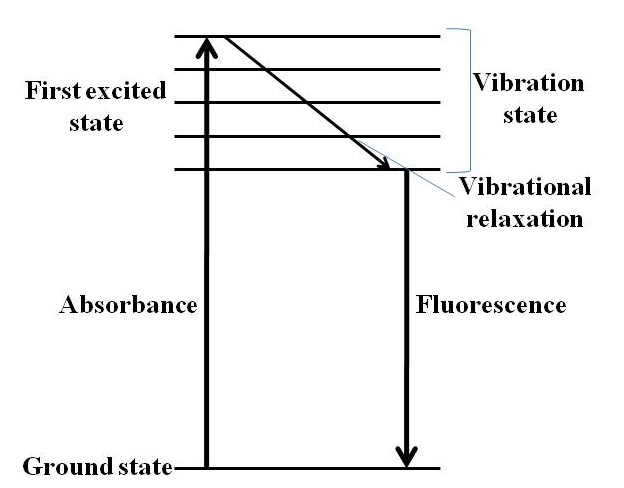
Instrumentation
A schematic of a basic design for measuring fluorescence is shown in Figure \(\PageIndex{46}\). The requirements for PL spectroscopy are a source of radiation, a means of selecting a narrow band of radiation, and a detector. Unlike optical absorbance spectroscopy, the detector must not be placed along the axis of the sample, but rather at 90º to the source. This is done to minimize the intensity of transmitted source radiation (light scattered by the sample) reaching the detector. Figure \(\PageIndex{46}\) shows two different ways of selecting the appropriate wavelength for excitation: a monochromator and a filter. In a fluorimeter the excitation and emission wavelengths are selected using absorbance or interference filters. In a spectrofluorimeterthe excitation and emission wavelengths are selected by a monochromator.
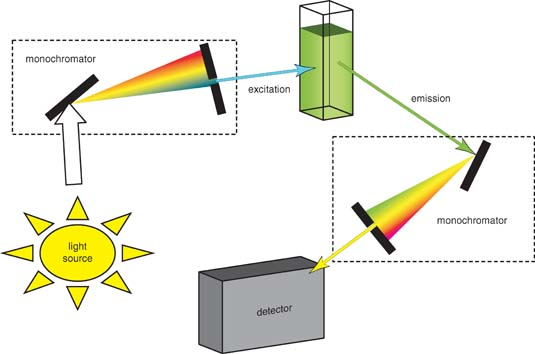
Excitation vs. Emission Spectra
PL spectra can be recorded in two ways: by measuring the intensity of emitted radiation as a function of the excitation wavelength, or by measuring the emitted radiation as a function of the the emission wavelength. In an excitation spectrum, a fixed wavelength is used to monitor emission while the excitation wavelength is varied. An excitation spectrum is nearly identical to a sample’s absorbance spectrum. In an emission spectrum, a fixed wavelength is used to excite the sample and the intensity of the emitted radiation is monitored as a function of wavelength.
Optical Absorbance Spectroscopy
PL spectroscopy data is frequently combined with optical absorbance spectroscopy data to produce a more detailed description of the band gap size of QDs. UV-visible spectroscopy is a specific kind of optical absorbance spectroscopy that measures the transitions from ground state to excited state. This is the opposite of PL spectroscopy, which measures the transitions from excited states to ground states. UV-visible spectroscopy uses light in the visible or ultraviolet range to excite electrons and measures the absorbance of radiation verses wavelength. A sharp peak in the UV-visible spectrum indicates the wavelength at which the sample best absorbs radiation.
As mentioned before, an excitation spectrum is a graph of emission intensity versus excitation wavelength. This spectrum often looks very similar to the absorbance spectrum and in some instances they are the exact same. However, slight differences in the theory behind these techniques do exist. Broadly speaking, an absorption spectrum measures wavelengths at which a molecule absorbs lights, while an excitation spectrum determines the wavelength of light necessary to produce emission or fluorescence from the sample, as monitored at a particular wavelength. It is quite possible then for peaks to appear in the absorbance spectrum that would not occur on the PL excitation spectrum.
Instrumentation
A schematic diagram for a UV-vis spectrometer is shown in Figure \(\PageIndex{47}\). Like PL spectroscopy, the instrument requires a source of radiation, a means of selecting a narrow band of radiation (monochromator), and a detector. Unlike PL spectroscopy, the detector is placed along the same axis as the sample, rather than being directed 90º away from it.
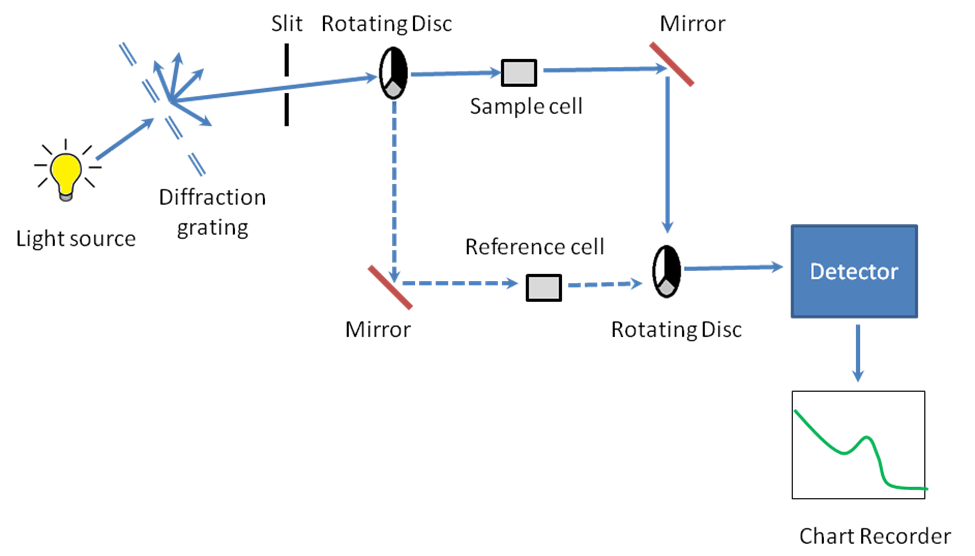
Sample Spectra
A UV-Vis spectrum, such as the one shown in Figure \(\PageIndex{48}\), can be used not only to determine the band gap of QDs, but to also determine QD size. Because QDs absorb different wavelengths of light based on the size of the particles, UV-Vis (and PL) spectroscopy can provide a convenient and inexpensive way to determine the band gap and/or size of the particle by using the peaks on the spectrum.
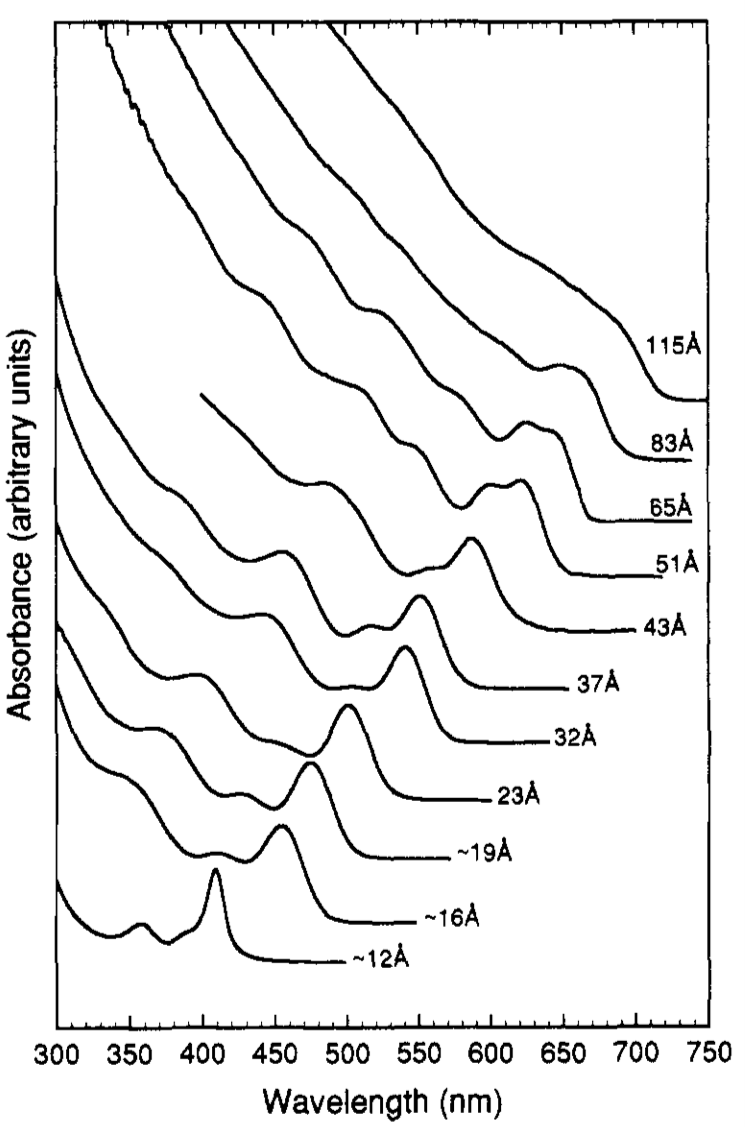
The highly tunable nature of QDs, as well as their high extinction coefficient, makes QDs well-suited to a large variety of applications and new technologies. QDs may find use as inorganic fluorophores in biological imaging, as tools to improve efficiency in photovoltaic devices, and even as a implementations for qubits in quantum computers. Knowing the band gap of QDs is essential to understanding how QDs may be used in these technologies. PL and optical absorbance spectroscopies provide ideal ways of obtaining this information.


