7.2: Structures of Element and Compound Semiconductors
- Page ID
- 55905
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A single crystal of either an elemental (e.g., silicon) or compound (e.g., gallium arsenide) semiconductor forms the basis of almost all semiconductor devices. The ability to control the electronic and opto-electronic properties of these materials is based on an understanding of their structure. In addition, the metals and many of the insulators employed within a microelectronic device are also crystalline.
Group IV (14) Elements
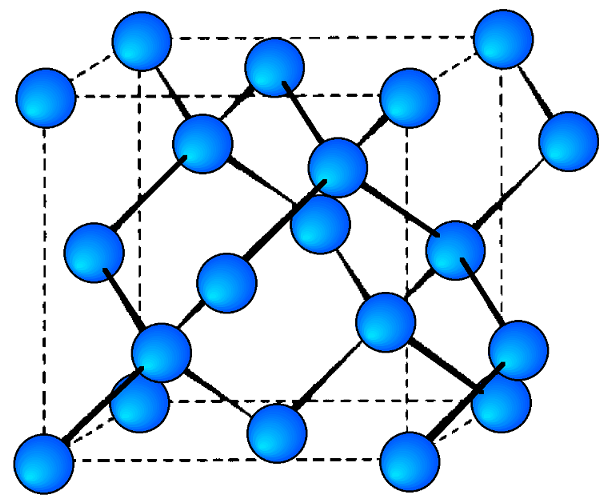
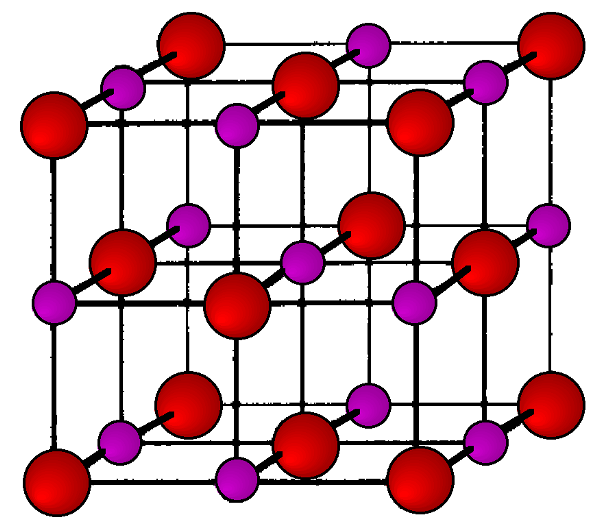
Each of the semiconducting phases of the group IV (14) elements, C (diamond), Si, Ge, and α-Sn, adopt the diamond cubic structure (Figure \(\PageIndex{1}\)). Their lattice constants (a, Å) and densities (ρ, g/cm3) are given in Table \(\PageIndex{1}\).
| Element | Lattice Parameter, a (Å) | Density (g/cm3) |
|---|---|---|
| carbon (diamond) | 3.56683(1) | 3.51525 |
| silicon | 5.4310201(3) | 2.319002 |
| germanium | 5.657906(1) | 5.3234 |
| tin (α-Sn) | 6.4892(1) |
As would be expected the lattice parameter increase in the order C < Si < Ge < α-Sn. Silicon and germanium form a continuous series of solid solutions with gradually varying parameters. It is worth noting the high degree of accuracy that the lattice parameters are known for high purity crystals of these elements. In addition, it is important to note the temperature at which structural measurements are made, since the lattice parameters are temperature dependent (Figure \(\PageIndex{1}\)). The lattice constant (a), in Å, for high purity silicon may be calculated for any temperature (T) over the temperature range 293 - 1073 K by the formula shown below.
\[ a_{T}\ =\ 5.4304\ +\ 1.8138 \times 10^{-5}\ (T- 298.15\ K)\ +\ 1.542 \times 10^{-9}\ (T-298.15\ K) \label{1} \]
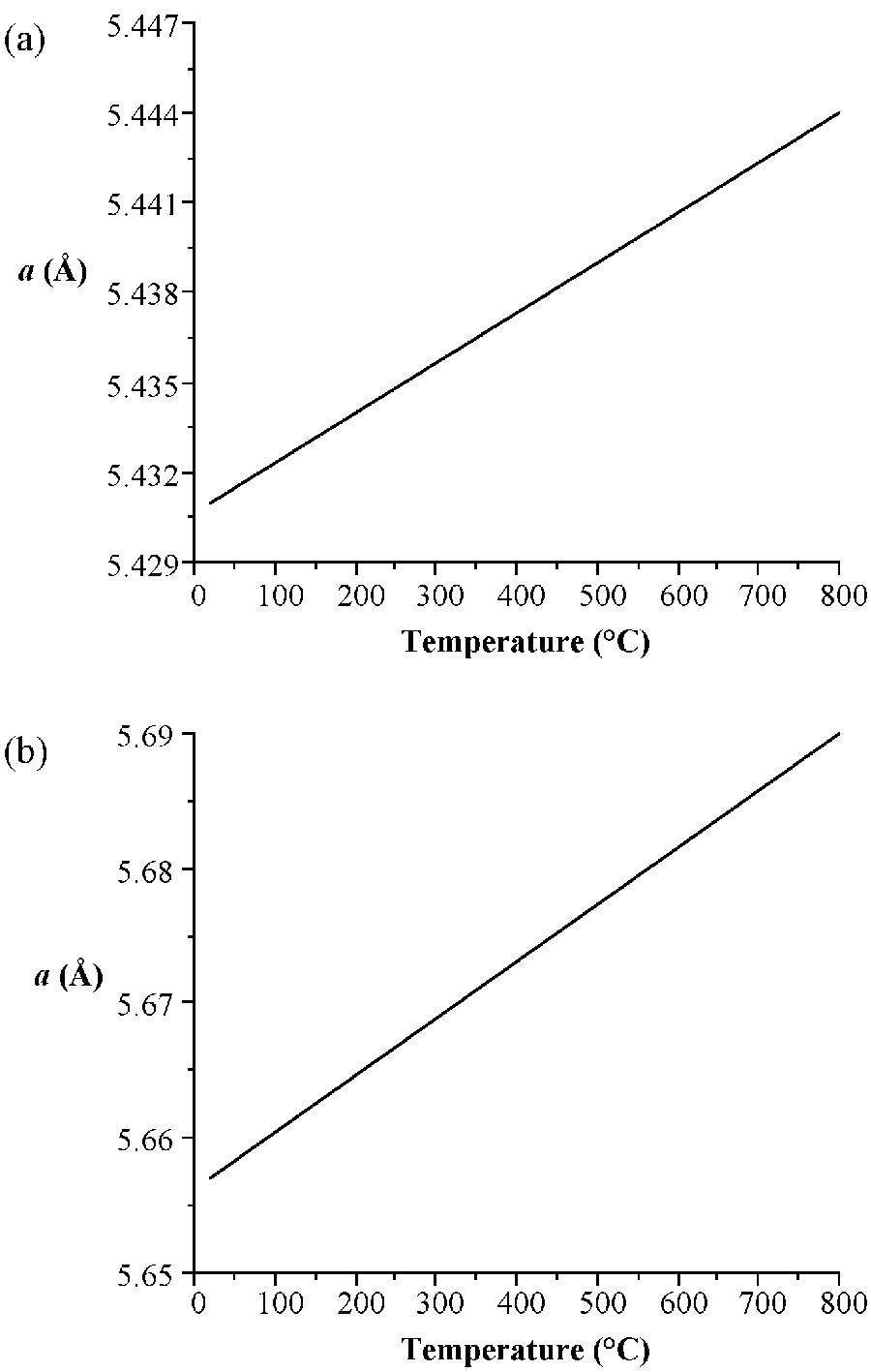
Even though the diamond cubic forms of Si and Ge are the only forms of direct interest to semiconductor devices, each exists in numerous crystalline high pressure and meta-stable forms. These are described along with their interconversions, in Table \(\PageIndex{2}\).
| Phase | Structure | Remarks |
|---|---|---|
| Si I | diamond cubic | stable at normal pressure |
| Si II | grey tin structure | formed from Si I or Si V above 14 GPa |
| Si III | cubic | metastable, formed from Si II above 10 GPa |
| Si IV | hexagonal | |
| Si V | unidentified | stable above 34 GPa, formed from Si II above 16 GPa |
| Si VI | hexagonal close packed | stable above 45 GPa |
| Ge I | diamond cubic | low-pressure phase |
| Ge II | β-tin structure | formed from Ge I above 10 GPa |
| Ge III | tetragonal | formed by quenching Ge II at low pressure |
| Ge IV | body centered | formed by quenching Ge II to 1 atm at 200 K |
Group III-V (13-15) Compounds
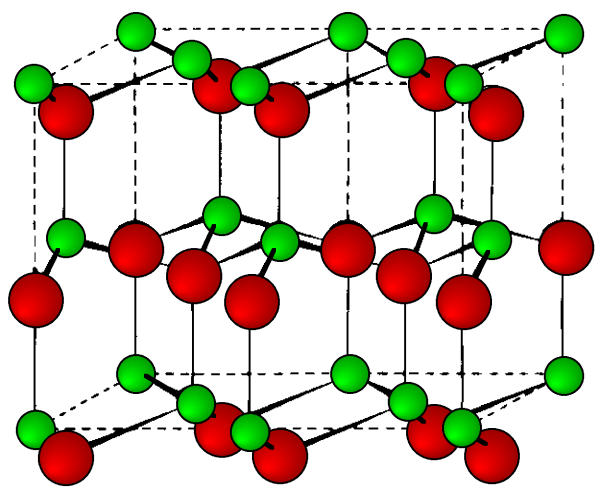
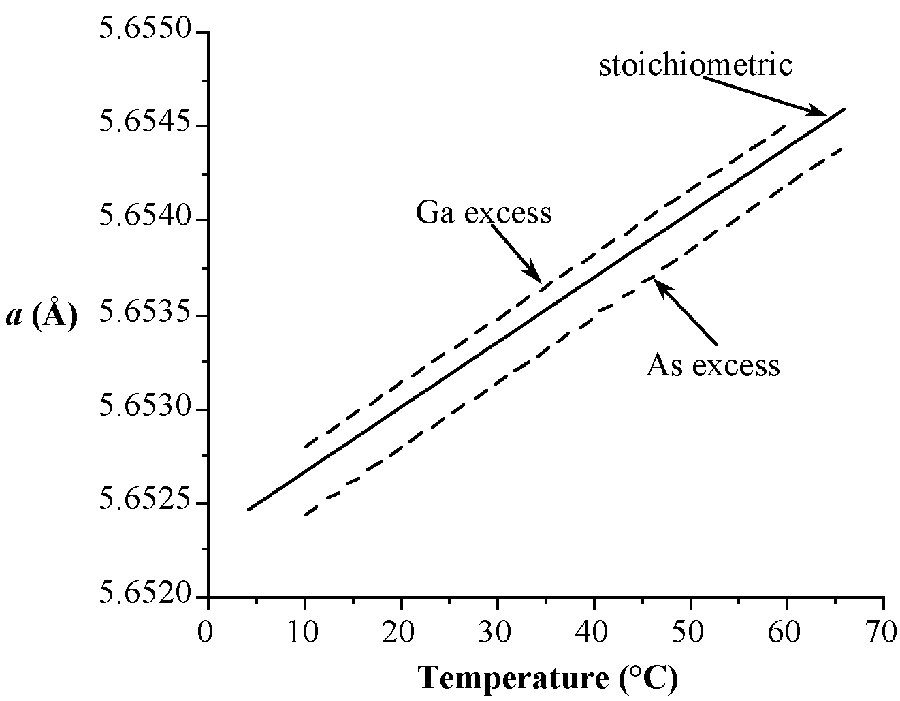
The stable phases for the arsenides, phosphides and antimonides of aluminum, gallium and indium all exhibit zinc blende structures (Figure \(\PageIndex{3}\)). In contrast, the nitrides are found as wurtzite structures (e.g., Figure \(\PageIndex{4}\)). The structure, lattice parameters, and densities of the III-V compounds are given in Table \(\PageIndex{3}\). It is worth noting that contrary to expectation the lattice parameter of the gallium compounds is smaller than their aluminum homolog; for GaAs a = 5.653 Å; AlAs a = 5.660 Å. As with the group IV elements the lattice parameters are highly temperature dependent; however, additional variation arises from any deviation from absolute stoichiometry. These effects are shown in Figure \(\PageIndex{4}\).
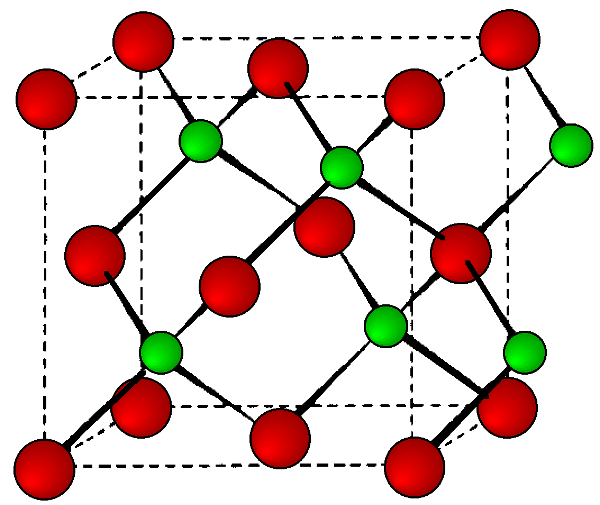
| Compound | Structure | Lattice Parameter (Å) | Density (g/cm3) |
|---|---|---|---|
| AIN | wurtzite | a = 3.11(1), c = 4.98(1) | 3.255 |
| AIP | zinc blende | a = 5.4635(4) | 2.40(1) |
| AIAs | zinc blende | a= 5.660 | 3.760 |
| AISb | zinc blende | a = 6.1355(1) | 4.26 |
| GaN | wurtzite | a = 3.190, c=5.187 | |
| GaP | zinc blende | a= 5.4505(2) | 4.138 |
| GaAs | zinc blende | a= 5.56325(2) | 5.3176(3) |
| InN | wurtzite | a= 3.5446, c= 5.7034 | 6.81 |
| InP | zinc blende | a= 5.868(1) | 4.81 |
| InAs | zinc blende | a= 6.0583 | 5.667 |
| InSb | zinc blende | a= 6.47937 | 5.7747(4) |
The homogeneity of structures of alloys for a wide range of solid solutions to be formed between III-V compounds in almost any combination. Two classes of ternary alloys are formed: IIIx-III1-x-V (e.g., Alx-Ga1-x-As) and III-V1-x-Vx (e.g., Ga-As1-x-Px) . While quaternary alloys of the type IIIx-III1-x-Vy-V1-y allow for the growth of materials with similar lattice parameters, but a broad range of band gaps. A very important ternary alloy, especially in optoelectronic applications, is Alx-Ga1-x-As and its lattice parameter (a) is directly related to the composition (x).
\[ a\ =\ 5.6533\ +\ 0.0078\ x \nonumber \]
Not all of the III-V compounds have well characterized high-pressure phases. however, in each case where a high-pressure phase is observed the coordination number of both the group III and group V element increases from four to six. Thus, AlP undergoes a zinc blende to rock salt transformation at high pressure above 170 kbar, while AlSb and GaAs form orthorhombic distorted rock salt structures above 77 and 172 kbar, respectively. An orthorhombic structure is proposed for the high-pressure form of InP (>133 kbar). Indium arsenide (InAs) undergoes two-phase transformations. The zinc blende structure is converted to a rock salt structure above 77 kbar, which in turn forms a β-tin structure above 170 kbar.
Group II-VI (12-16) Compounds
The structures of the II-VI compound semiconductors are less predictable than those of the III-V compounds (above), and while zinc blende structure exists for almost all of the compounds there is a stronger tendency towards the hexagonal wurtzite form. In several cases the zinc blende structure is observed under ambient conditions, but may be converted to the wurtzite form upon heating. In general the wurtzite form predominates with the smaller anions (e.g., oxides), while the zinc blende becomes the more stable phase for the larger anions (e.g., tellurides). One exception is mercury sulfide (HgS) that is the archetype for the trigonal cinnabar phase.Table \(\PageIndex{5}\) lists the stable phase of the chalcogenides of zinc, cadmium and mercury, along with their high temperature phases where applicable. Solid solutions of the II-VI compounds are not as easily formed as for the III-V compounds; however, two important examples are ZnSxSe1-x and CdxHg1-xTe.
| Compound | Structure | Lattice Parameter (Å) | Density (g/cm3) |
| ZnS | zinc blende | a= 5.410 | 4.075 |
| wurtzite | a = 3.822, c= 6.260 | 4.087 | |
| ZnSe | zinc blende | a = 5.668 | 5.27 |
| ZnTe | zinc blende | a = 6.10 | 5.636 |
| CdS | wurtzite | a = 4.136, c = 6.714 | 4.82 |
| CdSe | wurtzite | a = 4.300, c = 7.011 | 5.81 |
| CdTe | zinc blende | a = 6.482 | 5.87 |
| HgS | cinnabar | a = 4.149, c = 9.495 | |
| zinc blende | a = 5.851 | 7.73 | |
| HgSe | zinc blende | a = 6.085 | 8.25 |
| HgTe | zinc blende | a = 6.46 | 8.07 |
The zinc chalcogenides all transform to a cesium chloride structure under high pressures, while the cadmium compounds all form rock salt high-pressure phases (Figure \(\PageIndex{6}\)). Mercury selenide (HgSe) and mercury telluride (HgTe) convert to the mercury sulfide archetype structure, cinnabar, at high pressure.
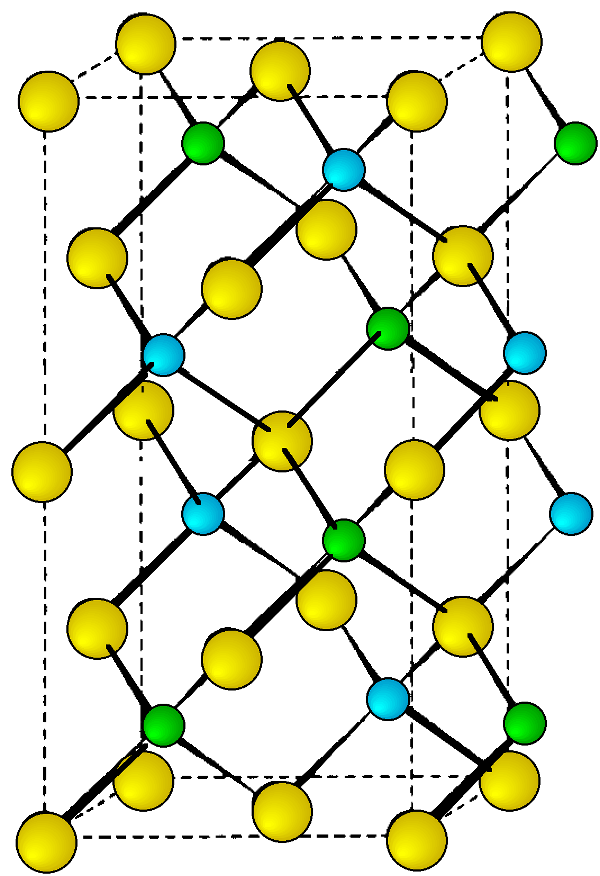
I-III-VI2 (11-13-16) Compounds
Nearly all I-III-VI2 compounds at room temperature adopt the chalcopyrite structure (Figure \(\PageIndex{7}\)). The cell constants and densities are given in Table \(\PageIndex{6}\). Although there are few reports of high temperature or high-pressure phases, AgInS2 has been shown to exist as a high temperature orthorhombic polymorph (a = 6.954, b = 8.264, and c = 6.683 Å), and AgInTe2 forms a cubic phase at high pressures.
| Compound | Lattice Parameter a (Å) | Lattice parameter c (Å) | Density (g cm3) |
| CuAlS2 | 5.32 | 10.430 | 3.45 |
| CuAlSe2 | 5.61 | 10.92 | 4.69 |
| CuAlTe2 | 5.96 | 11.77 | 5.47 |
| CuGaS2 | 5.35 | 10.46 | 4.38 |
| CuGaSe2 | 5.61 | 11.00 | 5.57 |
| CuGaTe2 | 6.00 | 11.93 | 5.95 |
| CuInS2 | 5.52 | 11.08 | 4.74 |
| CuInSe2 | 5.78 | 11.55 | 5.77 |
| CuInTe2 | 6.17 | 12.34 | 6.10 |
| AgAlS2 | 6.30 | 11.84 | 6.15 |
| AgGaS2 | 5.75 | 10.29 | 4.70 |
| AgGaSe2 | 5.98 | 10.88 | 5.70 |
| AgGaTe2 | 6.29 | 11.95 | 6.08 |
| AgInS2 | 5.82 | 11.17 | 4.97 |
| AgInSe2 | 6.095 | 11.69 | 5.82 |
| AgInTe2 | 6.43 | 12.59 | 6.96 |
Of the I-III-VI2 compounds, the copper indium chalcogenides (CuInE2) are certainly the most studied for their application in solar cells. One of the advantages of the copper indium chalcogenide compounds is the formation of solid solutions (alloys) of the formula CuInE2-xE'x, where the composition variable (x) varies from 0 to 2. The CuInS2-xSex and CuInSe2-xTex systems have also been examined, as has the CuGayIn1-yS2-xSex quaternary system. As would be expected from a consideration of the relative ionic radii of the chalcogenides the lattice parameters of the CuInS2-xSex alloy should increase with increased selenium content. Vergard's law requires the lattice constant for a linear solution of two semiconductors to vary linearly with composition (e.g., as is observed for AlxGa1-xAs), however, the variation of the tetragonal lattice constants (a and c) with composition for CuInS2-xSx are best described by the parabolic relationships.
\[ a\ =\ 5.532\ +\ 0.0801x\ +\ 0.026 x^{2} \nonumber \]
\[ c\ =\ 11.156\ +\ 0.1204x\ +\ 0.0611 x^{2} \nonumber \]
A similar relationship is observed for the CuInSe2-xTex alloys.
\[ a\ =\ 5.783\ +\ 0.1560 x\ +\ 0.0212x^{2} \nonumber \]
\[ c\ =\ 11.628\ +\ 0.3340x\ +\ 0.0277x^{2} \nonumber \]
The large difference in ionic radii between S and Te (0.37 Å) prevents formation of solid solutions in the CuInS2-xTex system, however, the single alloy CuInS1.5Te0.5 has been reported.
Orientation Effects
Once single crystals of high purity silicon or gallium arsenide are produced they are cut into wafers such that the exposed face of these wafers is either the crystallographic {100} or {111} planes. The relative structure of these surfaces are important with respect to oxidation, etching and thin film growth. These processes are orientation-sensitive; that is, they depend on the direction in which the crystal slice is cut.
Atom Density and Dangling Bonds
The principle planes in a crystal may be differentiated in a number of ways, however, the atom and/or bond density are useful in predicting much of the chemistry of semiconductor surfaces. Since both silicon and gallium arsenide are fcc structures and the {100} and {111} are the only technologically relevant surfaces, discussions will be limited to fcc {100} and {111}.
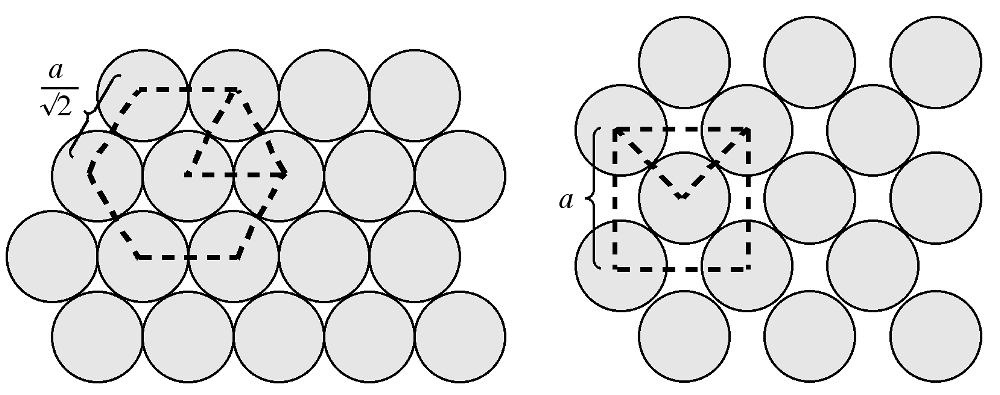
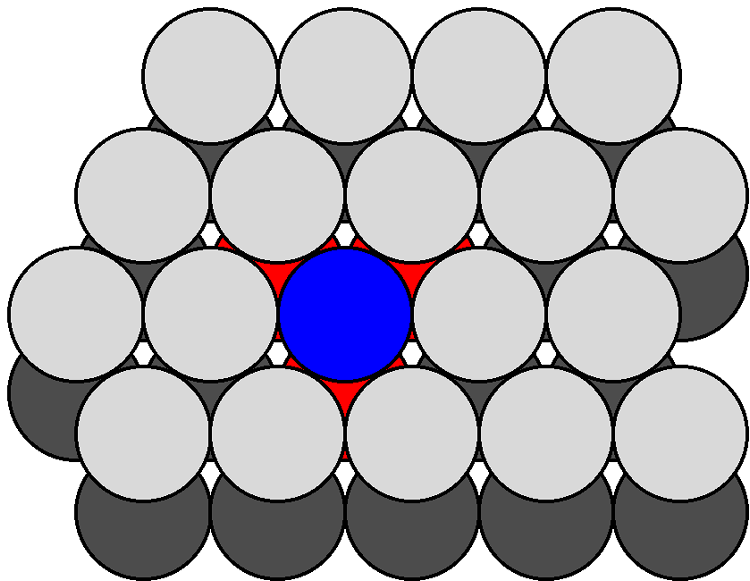
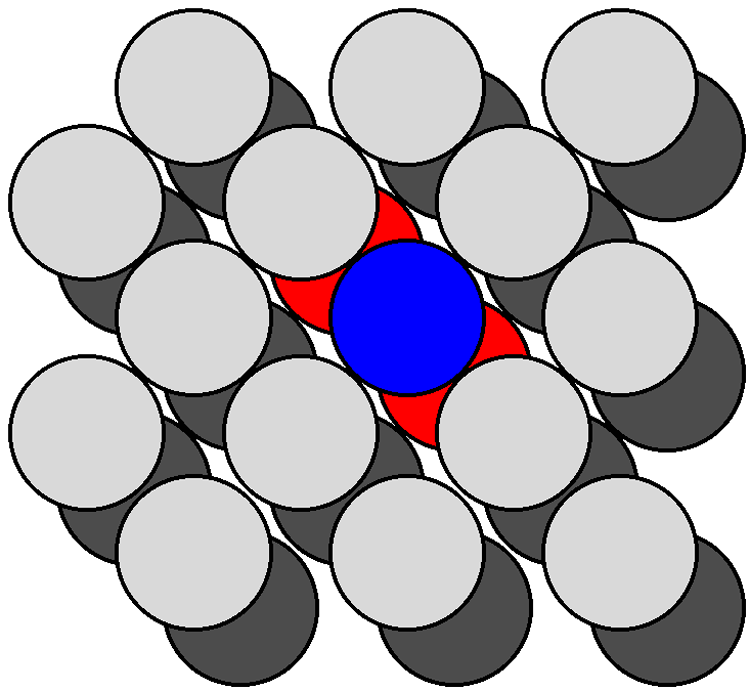
The atom density of a surface may be defined as the number of atoms per unit area. Figure shows a schematic view of the {111} and {100} planes in a fcc lattice. The {111} plane consists of a hexagonal close packed array in which the crystal directions within the plane are oriented at 60° to each other. The hexagonal packing and the orientation of the crystal directions are indicated in Figure \(\PageIndex{8}\) b as an overlaid hexagon. Given the intra-planar inter-atomic distance may be defined as a function of the lattice parameter, the area of this hexagon may be readily calculated. For example in the case of silicon, the hexagon has an area of 38.30 Å2. The number of atoms within the hexagon is three: the atom in the center plus 1/3 of each of the six atoms at the vertices of the hexagon (each of the atoms at the hexagons vertices is shared by three other adjacent hexagons). Thus, the atom density of the {111} plane is calculated to be 0.0783 Å-2. Similarly, the atom density of the {100} plane may be calculated. The {100} plane consists of a square array in which the crystal directions within the plane are oriented at 90° to each other. Since the square is coincident with one of the faces of the unit cell the area of the square may be readily calculated. For example in the case of silicon, the square has an area of 29.49 Å2. The number of atoms within the square is 2: the atom in the center plus 1/4 of each of the four atoms at the vertices of the square (each of the atoms at the corners of the square are shared by four other adjacent squares). Thus, the atom density of the {100} plane is calculated to be 0.0678 Å-2. While these values for the atom density are specific for silicon, their ratio is constant for all diamond cubic and zinc blende structures: {100}:{111} = 1:1.155. In general, the fewer dangling bonds the more stable a surface structure.
An atom inside a crystal of any material will have a coordination number (n) determined by the structure of the material. For example, all atoms within the bulk of a silicon crystal will be in a tetrahedral four-coordinate environment (n = 4). However, at the surface of a crystal the atoms will not make their full compliment of bonds. Each atom will therefore have less nearest neighbors than an atom within the bulk of the material. The missing bonds are commonly called dangling bonds. While this description is not particularly accurate it is, however, widely employed and as such will be used herein. The number of dangling bonds may be defined as the difference between the ideal coordination number (determined by the bulk crystal structure) and the actual coordination number as observed at the surface.
Figure \(\PageIndex{9}\) shows a section of the {111} surfaces of a diamond cubic lattice viewed perpendicular to the {111} plane. The atoms within the bulk have a coordination number of four. In contrast, the atoms at the surface (e.g., the atom shown in blue in Figure \(\PageIndex{10}\) are each bonded to just three other atoms (the atoms shown in red in Figure), thus each surface atom has one dangling bond. As can be seen from Figure \(\PageIndex{10}\), which shows the atoms at the {100} surface viewed perpendicular to the {100} plane, each atom at the surface (e.g., the atom shown in blue in Figure \(\PageIndex{9}\) is only coordinated to two other atoms (the atoms shown in red in Figure \(\PageIndex{10}\), leaving two dangling bonds per atom. It should be noted that the same number of dangling bonds are found for the {111} and {100} planes of a zinc blende lattice. The ratio of dangling bonds for the {100} and {111} planes of all diamond cubic and zinc blende structures is {100}:{111} = 2:1. Furthermore, since the atom densities of each plane are known then the ratio of the dangling bond densities is determined to be: {100}:{111} = 1:0.577.
Silicon
For silicon, the {111} planes are closer packed than the {100} planes. As a result, growth of a silicon crystal is therefore slowest in the <111> direction, since it requires laying down a close packed atomic layer upon another layer in its closest packed form. As a consequence <111> Si is the easiest to grow, and therefore the least expensive.
The dissolution or etching of a crystal is related to the number of broken bonds already present at the surface: the fewer bonds to be broken in order to remove an individual atom from a crystal, the easier it will be to dissolve the crystal. As a consequence of having only one dangling bond (requiring three bonds to be broken) etching silicon is slowest in the <111> direction. The electronic properties of a silicon wafer are also related to the number of dangling bonds.
Silicon microcircuits are generally formed on a single crystal wafer that is diced after fabrication by either sawing part way through the wafer thickness or scoring (scribing) the surface, and then physically breaking. The physical breakage of the wafer occurs along the natural cleavage planes, which in the case of silicon are the {111} planes.
Gallium Arsenide
The zinc blende lattice observed for gallium arsenide results in additional considerations over that of silicon. Although the {100} plane of GaAs is structurally similar to that of silicon, two possibilities exist: a face consisting of either all gallium atoms or all arsenic atoms. In either case the surface atoms have two dangling bonds, and the properties of the face are independent of whether the face is gallium or arsenic.
The {111} plane also has the possibility of consisting of all gallium or all arsenic. However, unlike the {100} planes there is a significant difference between the two possibilities. Figure \(\PageIndex{11}\) shows the gallium arsenide structure represented by two interpenetrating fcc lattices. The [111] axis is vertical within the plane of the page. Although the structure consists of alternate layers of gallium and arsenic stacked along the [111] axis, the distance between the successive layers alternates between large and small. Assigning arsenic as the parent lattice the order of the layers in the [111] direction is As-Ga-As-Ga-As-Ga, while in the [111] direction the layers are ordered, Ga-As-Ga-As-Ga-As (Figure \(\PageIndex{11}\)).In silicon these two directions are of course identical. The surface of a crystal would be either arsenic, with three dangling bonds, or gallium, with one dangling bond. Clearly, the latter is energetically more favorable. Thus, the (111) plane shown in Figure \(\PageIndex{11}\) is called the (111) Ga face. Conversely, the [111] plane would be either gallium, with three dangling bonds, or arsenic, with one dangling bond. Again, the latter is energetically more favorable and the [111] plane is therefore called the (111) As face.
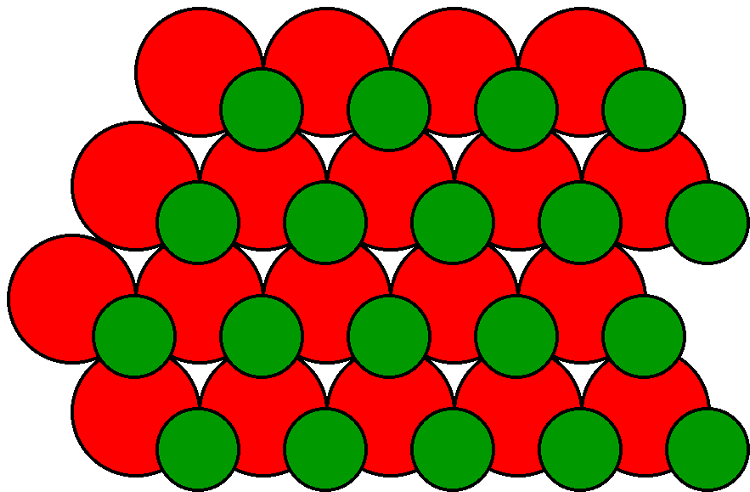
The (111) As is distinct from that of (111) Ga due to the difference in the number of electrons at the surface. As a consequence, the (111) As face etches more rapidly than the (111) Ga face. In addition, surface evaporation below 770 °C occurs more rapidly at the (111) As face.


