4.6: Mössbauer Spectroscopy
- Page ID
- 55885
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In 1957 Rudolf Mössbauer achieved the first experimental observation of the resonant absorption and recoil-free emission of nuclear γ-rays in solids during his graduate work at the Institute for Physics of the Max Planck Institute for Medical Research in Heidelberg Germany. Mössbauer received the 1961 Nobel Prize in Physics for his research in resonant absorption of γ-radiation and the discovery of recoil-free emission a phenomenon that is named after him. The Mössbauer effect is the basis of Mössbauer spectroscopy.
The Mössbauer effect can be described very simply by looking at the energy involved in the absorption or emission of a γ-ray from a nucleus. When a free nucleus absorbs or emits a γ-ray to conserve momentum the nucleus must recoil, so in terms of energy:
\[ E_{ \gamma - ray} \ = \ E_{\text{nuclear transition}}\ -\ E_{\text{recoil}} \label{1} \]
When in a solid matrix the recoil energy goes to zero because the effective mass of the nucleus is very large and momentum can be conserved with negligible movement of the nucleus. So, for nuclei in a solid matrix:
\[ E_{\gamma - ray} \ =\ E_{\text{nuclear transition}} \label{2} \]
This is the Mössbauer effect which results in the resonant absorption/emission of γ-rays and gives us a means to probe the hyperfine interactions of an atoms nucleus and its surroundings.
A Mössbauer spectrometer system consists of a γ-ray source that is oscillated toward and away from the sample by a “Mössbauer drive”, a collimator to filter the γ-rays, the sample, and a detector.
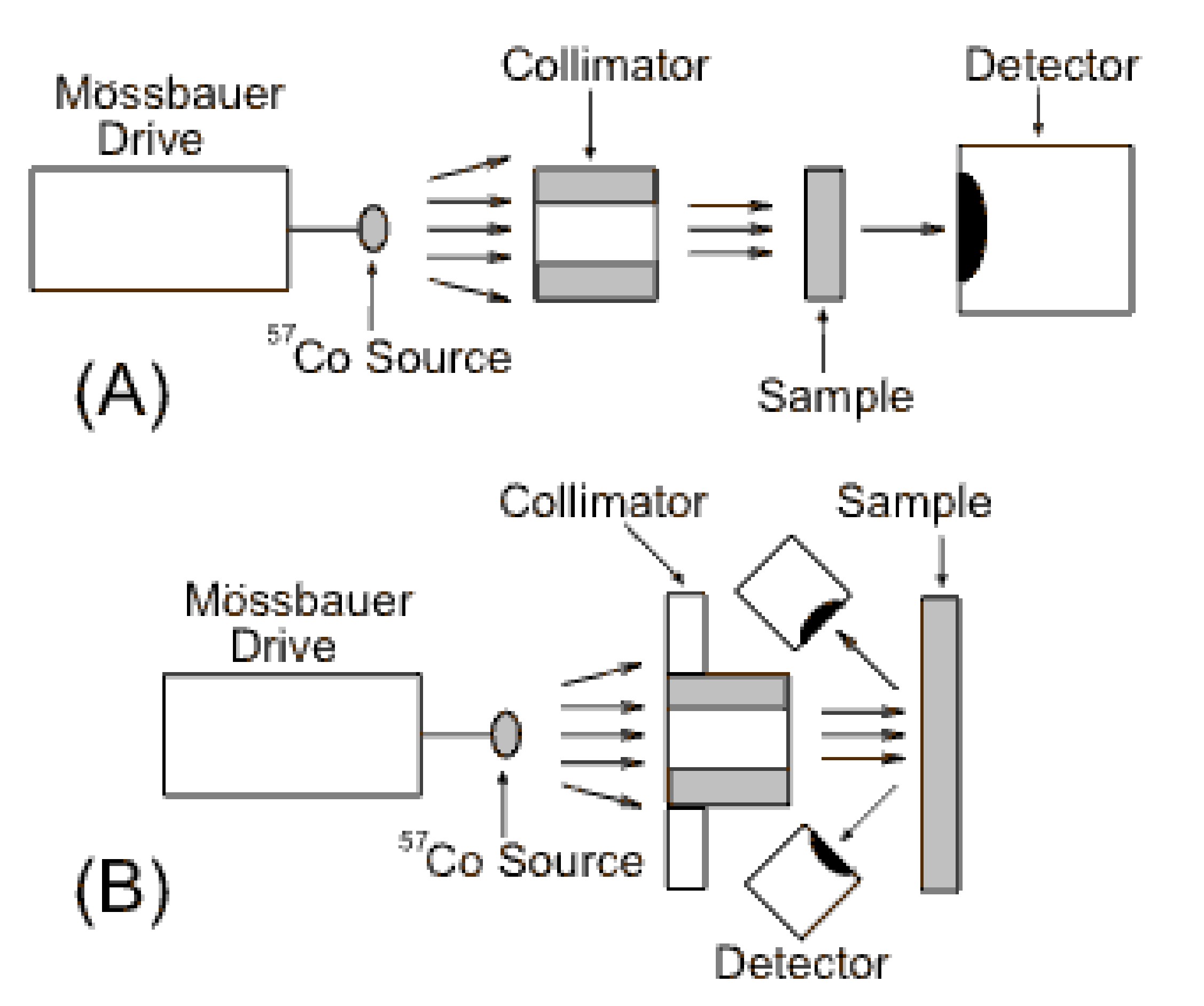
Figure \(\PageIndex{2}\) hows the two basic set ups for a Mössbauer spectrometer. The Mössbauer drive oscillates the source so that the incident γ-rays hitting the absorber have a range of energies due to the doppler effect. The energy scale for Mössbauer spectra (x-axis) is generally in terms of the velocity of the source in mm/s. The source shown (57Co) is used to probe 57Fe in iron containing samples because 57Co decays to 57Fe emitting a γ-ray of the right energy to be absorbed by 57Fe. To analyze other Mössbauer isotopes other suitable sources are used. Fe is the most common element examined with Mössbauer spectroscopy because its 57Fe isotope is abundant enough (2.2), has a low energy γ-ray, and a long lived excited nuclear state which are the requirements for observable Mössbauer spectrum. Other elements that have isotopes with the required parameters for Mössbauer probing are seen in Table \(\PageIndex{1}\).
| Most commonly examined elements | Fe, Ru, W, Ir, Au, Sn, Sb, Te, I, W, Ir, Eu, Gd, Dy, Er, Yb, Np |
| Elements that exhibit Mössbauer effect | K, Ni, Zn, Ge, Kr, Tc, Ag, Xe, Cs, Ba, La, Hf, Ta, Re, Os, Pt, Hg, Ce, Pr, Nd, Sm, Tb, Ho, Tm, Lu, Th, Pa, U, Pu, Am |
Mössbauer Spectra
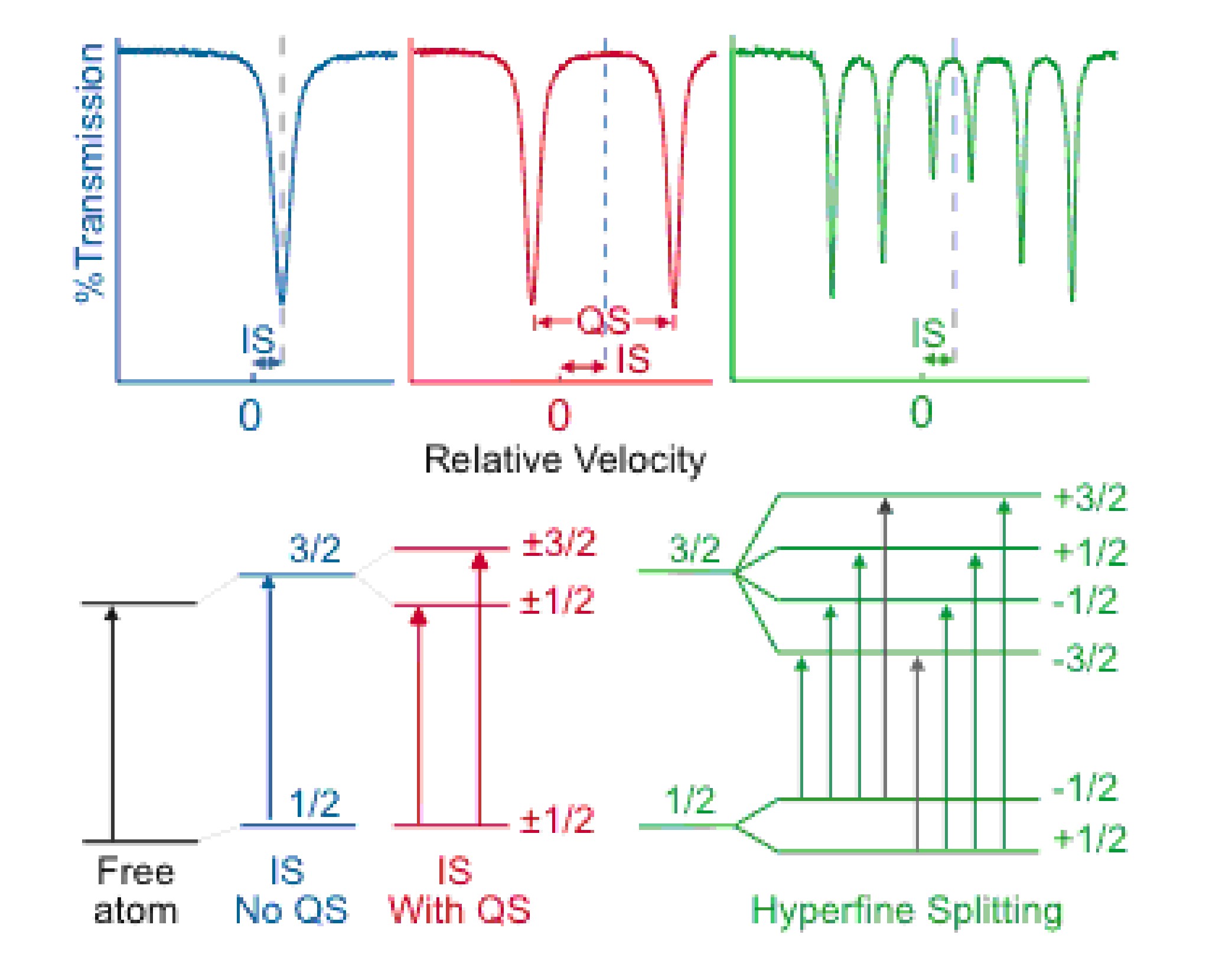
The primary characteristics looked at in Mössbauer spectra are isomer shift (IS), quadrupole splitting (QS), and magnetic splitting (MS or hyperfine splitting). These characteristics are effects caused by interactions of the absorbing nucleus with its environment.
Isomer shift is due to slightly different nuclear energy levels in the source and absorber due to differences in the s-electron environment of the source and absorber. The oxidation state of an absorber nucleus is one characteristic that can be determined by the IS of a spectra. For example due to greater d electron screening Fe2+ has less s-electron density than Fe3+ at its nucleus which results in a greater positive IS for Fe2+.
For absorbers with nuclear angular momentum quantum number I > ½ the non-spherical charge distribution results in quadrupole splitting of the energy states. For example Fe with a transition from I=1/2 to 3/2 will exhibit doublets of individual peaks in the Mössbauer spectra due to quadrupole splitting of the nuclear states as shown in red in Figure \(\PageIndex{2}\).
In the presence of a magnetic field the interaction between the nuclear spin moments with the magnetic field removes all the degeneracy of the energy levels resulting in the splitting of energy levels with nuclear spin I into 2I + 1 sublevels. Using Fe for an example again, magnetic splitting will result in a sextet as shown in green in Figure \(\PageIndex{2}\). Notice that there are 8 possible transitions shown, but only 6 occur. Due to the selection rule ІΔmIІ = 0, 1, the transitions represented as black arrows do not occur.
Synthesis of Magnetite Nanoparticles
Numerous schemes have been devised to synthesize magnetite nanoparticles (nMag). The different methods of nMag synthesis can be generally grouped as aqueous or non-aqueous according to the solvents used. Two of the most widely used and explored methods for nMag synthesis are the aqueous co-precipitation method and the non-aqueous thermal decomposition method.
The co-precipitation method of nMag synthesis consists of precipitation of Fe3O4 (nMag) by addition of a strong base to a solution of Fe2+ and Fe3+ salts in water. This method is very simple, inexpensive and produces highly crystalline nMag. The general size of nMag produced by co-precipitation is in the 15 to 50 nm range and can be controlled by reaction conditions, however a large size distribution of nanoparticles is produced by this method. Aggregation of particles is also observed with aqueous methods.
The thermal decomposition method consists of the high temperature thermal decomposition of an iron-oleate complex derived from an iron precursor in the presence of surfactant in a high boiling point organic solvent under an inert atmosphere. For the many variations of this synthetic method many different solvents and surfactants are used. However, in most every method nMag is formed through the thermal decomposition of an iron-oleate complex to form highly crystalline nMag in the 5 to 40 nm range with a very small size distribution. The size of nMag produced is a function of reaction temperature, the iron to surfactant ratio, and the reaction time, and various methods are used that achieve good size control by manipulation of these parameters. The nMag synthesized by organic methods is soluble in organic solvents because the nMag is stabilized by a surfactant surface coating with the polar head group of the surfactant attached to and the hydrophobic tail extending away from the nMag (Figure \(\PageIndex{3}\)). An example of a thermal decomposition method is shown in Figure \(\PageIndex{3}\).

Mössbauer Analysis of Iron Oxide Nanoparticles
Spectra and Formula Calculations
Due to the potential applications of magnetite nanoparticles (Fe3O4, nMag) many methods have been devised for its synthesis. However, stoichiometric Fe3O4 is not always achieved by different synthetic methods. B-site vacancies introduced into the cubic inverse spinel crystal structure of nMag result in nonstoichiometric iron oxide of the formula (Fe3+)A(Fe(1-3x)2+ Fe(1+2X)3+Øx)BO4 where Ø represents B-site vacancy. The magnetic susceptibility which is key to most nMag applications decreases with increased B-site vacancy hence the extent of B-site vacancy is important. The very high sensitivity of the Mössbauer spectrum to the oxidation state and site occupancy of Fe3+ in cubic inverse spinel iron oxides makes Mössbauer spectroscopy valuable for addressing the issues of whether or not the product of a synthetic method is actually nMag and the extent of B-site vacancy.
As with most analysis using multiple instrumental methods in conjunction is often helpful. This is exemplified by the use of XRD along with Mössbauer spectroscopy in the following analysis. Figure \(\PageIndex{4}\) shows the XRD results and Mössbauer spectra “magnetite” samples prepared by a Fe2+/Fe3+ co-precipitation (Mt025), hematite reduction by hydrogen (MtH2) and hematite reduction with coal(MtC). The XRD analysis shows MtH2 and MT025 exhibiting only magnetite peaks while MtC shows the presence of magnetite, maghemite, and hematite. This information becomes very useful when fitting peaks to the Mössbauer spectra because it gives a chemical basis for peak fitting parameters and helps to fit the peaks correctly.
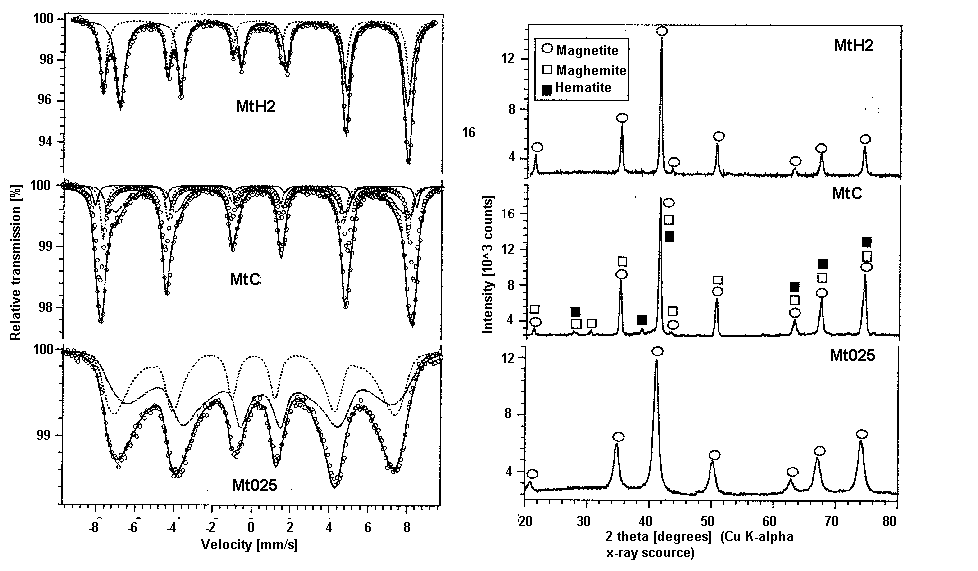
Being that the iron occupies two local environments, the A-site and B site, and two species (Fe2+ and Fe3+) occupy the B-site one might expect the spectrum to be a combination of 3 spectra, however delocalization of electrons or electron hopping between Fe2+ and Fe3+ in the B site causes the nuclei to sense an average valence in the B site thus the spectrum are fitted with two curves accordingly. This is most easily seen in the Mt025 spectrum. The two fitted curves correspond to Fe3+ in the A-site and mixed valance Fe2.5+ in the B-site. The isomer shift of the fitted curves can be used to determined which curve corresponds to which valence. The isomer shift relative to the top fitted curve is reported to be 0.661 and the bottom fitted curve is 0.274 relative to αFe thus the top fitted curve corresponds to less s-electron dense Fe2.5+. The magnetic splitting is quite apparent. In each of the spectra, six peaks are present due to magnetic splitting of the nuclear energy states as explained previously. Quadrupole splitting is not so apparent, but actually is present in the spectra. The three peaks to the left of the center of a spectrum should be spaced the same as those to the right due to magnetic splitting alone since the energy level spacing between sublevels is equal. This is not the case in the above spectra, because the higher energy I = 3/2 sublevels are split unevenly due to magnetic and quadrupole splitting interactions.
Once the peaks have been fitted appropriately, determination of the extent of B-site vacancy in (Fe3+)A(Fe(1-3x)2+ Fe(1+2X)3+Øx)BO4 is a relatively simple matter. All one has to due to determine the number of vacancies (x) is solve the equation:
\[ \frac{RA_{B}}{RA_{A}} = \frac{2-6x}{1-5x} \label{3} \]
where RAB or A = relative area
\[ \frac{Area\ A\ or\ B\ site\ curve}{Area\ of\ both\ curves} \label{4} \]
of the curve for the B or A site respectively
The reasoning for this equation is as follows. Taking into account that the mixed valance Fe2.5+ curve is a result of paired interaction between Fe2+ and Fe3+ the nonstochiometric chemical formula is (Fe3+)A(Fe(1-3x)2+Fe(1+2X)3+Øx)BO4. The relative intensity (or relative area) of the Fe-A and Fe-B curves is very sensitive to stoichiometry because vacancies in the B-site reduce the Fe-A curve and increase Fe-B curve intensities. This is due to the unpaired Fe5x3+ adding to the intensity of the Fe-A curve rather than the Fe-B curve. Since the relative area is directly proportional to the number of Fe contributing to the spectrum the ratio of the relative areas is equal to stoichiometric ratio of Fe2.5+ to Fe3+, which yields the above formula.
Example Calculation:
For MtH2 RAA/RAB = 1.89
Plugging x into the nonstoichiometric iron oxide formula yeilds:
\[ \frac{RA_{B}}{RA_{A}} = \frac{2-6x}{1-5x} \label{5} \]
solving for x yields
\[ x=\frac{2-\frac{RA_{A}}{RA_{B}}}{5 \frac{RA_{A}}{RA_{B}}\ +\ 6} \label{6} \]
(Fe3+)A(Fe 1.95722+ Fe0.03563+)BO4 (very close to stoichiometric)
| Sample | RAB/RAA | X | Chemical Formula |
|---|---|---|---|
| MtH2 | 1.89 | 0.007 | (Fe3+)A(Fe0.9792+Fe1.0143+)BO4 |
| MtC | 1.66 | 0.024 | (Fe3+)A(Fe0.9292+Fe1.0483+)BO4 |
| Mt 025 | 1.60 | 0.029 | (Fe3+)A(Fe0.9142+Fe1.0573+)BO4 |
Chemical Formulas of Nonstoichiometric Iron Oxide Nanoparticles from Mössbauer Spectroscopy
Chemical Formula Determination
Magnetite (Fe3O4) nanoparticles (n-Mag) are nanometer sized, superparamagnetic, have high saturation magnetization, high magnetic susceptibility, and low toxicity. These properties could be utilized for many possible applications; hence, n-Mag has attracted much attention in the scientific community. Some of the potential applications include drug delivery, hyperthermia agents, MRI contrast agents, cell labeling, and cell separation to name a few.
The crystal structure of n-Mag is cubic inverse spinel with Fe3+ cations occupying the interstitial tetrahedral sites(A) and Fe3+ along with Fe2+ occupying the interstitial octahedral sites(B) of an FCC latticed of O2-. Including the site occupation and charge of Fe, the n-Mag chemical formula can be written (Fe3+)A(Fe2+Fe3+)BO4. Non-stoichiometric iron oxide results from B-site vacancies in the crystal structure. To maintain balanced charge and take into account the degree of B-site vacancies the iron oxide formula is written (Fe3+)A(Fe(1-3x)2+ Fe(1+2X)3+Øx)BO4 where Ø represents B-site vacancy. The extent of B-site vacancy has a significant effect on the magnetic properties of iron oxide and in the synthesis of n-Mag stoichiometric iron oxide is not guaranteed; therefore, B-site vacancy warrants attention in iron oxide characterization, and can be addressed using Mössbauer spectroscopy.


