4.1: Magnetism
- Page ID
- 55872
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Magnetics
Magnetic Moments
The magnetic moment of a material is the incomplete cancelation of the atomic magnetic moments in that material. Electron spin and orbital motion both have magnetic moments associated with them (Figure \(\PageIndex{1}\)) but in most atoms the electronic moments are oriented usually randomly so that overall in the material they cancel each other out (Figure \(\PageIndex{2}\) ) this is called diamagnetism.

If the cancelation of the moments is incomplete then the atom has a net magnetic moment. There are many subclasses of magnetic ordering such as para-, superpara-, ferro-, antiferro- or ferromagnetism which can be displayed in a material and which usually depends, upon the strength and type of magnetic interactions and external parameters such as temperature and crystal structure atomic content and the magnetic environment which a material is placed in.
\[ \mu _{B} \ =\ \frac{eh}{4\pi m} \ = \ 9.72 \times 10^{-23} J/T \label{1} \]
The magnetic moments of atoms, molecules or formula units are often quoted in terms of the Bohr magneton, which is equal to the magnetic moment due to electron spin
Magnetization
The magnetism of a material, the extent that which a material is magnetic, is not a static quantity, but varies compared to the environment that a material is placed in. It is similar to the temperature of a material. For example if a material is placed in an oven it will heat up to a temperature similar to that of the ovens. However the speed of heating of that material, and also that of cooling are determined by the atomic structure of the material. The magnetization of a material is similar. When a material is placed in a magnetic field it maybe become magnetized to an extent and retain that magnetization after it is removed from the field. The extent of magnetization, and type of magnetization and the length of time that a material remains magnetized, depends again on the atomic makeup of the material.
Measuring a materials magnetism can be done on a micro or macro scale. Magnetism is measured over two parameters direction and strength. Thus magnetization has a vector quantity. The simplest form of a magnetometer is a compass. It measures the direction of a magnetic field. However more sophisticated instruments have been developed which give a greater insight into a materials magnetism.
So what exactly are you reading when you observe the output from a magnetometer?
The magnetism of a sample is called the magnetic moment of that sample and will be called that from now on. The single value of magnetic moment for the sample, is a combination of the magnetic moments on the atoms within the sample ( Figure \(\PageIndex{3}\) ), it is also the type and level of magnetic ordering and the physical dimensions of the sample itself.

The "intensity of magnetization", M, is a measure of the magnetization of a body. It is defined as the magnetic moment per unit volume or
\[ M \ =\ m/V \label{2} \]
with units of Am (emucm3 in cgs notation).
A material contains many atoms and their arrangement affects the magnetization of that material. In Figure \(\PageIndex{4}\) (a) a magnetic moment m is contained in unit volume. This has a magnetization of m Am. Figure \(\PageIndex{4}\) (b) shows two such units, with the moments aligned parallel. The vector sum of moments is 2m in this case, but as the both the moment and volume are doubled M remains the same. In Figure \(\PageIndex{4}\) (c) the moments are aligned antiparallel. The vector sum of moments is now 0 and hence the magnetization is 0 Am.
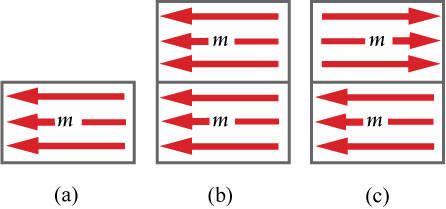
Scenarios (b) and (c) are a simple representation of ferro- and antiferromagnetic ordering. Hence we would expect a large magnetization in a ferromagnetic material such as pure iron and a small magnetization in an antiferromagnet such as γ-Fe2O3
Magnetic Response
When a material is passed through a magnetic field it is affected in two ways:
- Through its susceptibility.
- Through its permeability
Magnetic Susceptibility
The concept of magnetic moment is the starting point when discussing the behavior of magnetic materials within a field. If you place a bar magnet in a field it will experience a torque or moment tending to align its axis in the direction of the field. A compass needle behaves in the same way. This torque increases with the strength of the poles and their distance apart. So the value of magnetic moment tells you, in effect, 'how big a magnet' you have.

If you place a material in a weak magnetic field, the magnetic field may not overcome the binding energies that keep the material in a non magnetic state. This is because it is energetically more favorable for the material to stay exactly the same. However, if the strength of the magnetic moment is increased, the torque acting on the smaller moments in the material, it may become energetically more preferable for the material to become magnetic. The reasons that the material becomes magnetic depends on factors such as crystal structure the temperature of the material and the strength of the field that it is in. However a simple explanation of this is that as the magnetic moment strength increases it becomes more favorable for the small fields to align themselves along the path of the magnetic field, instead of being opposed to the system. For this to occur the material must rearrange its magnetic makeup at the atomic level to lower the energy of the system and restore a balance.
It is important to remember that when we consider the magnetic susceptibility and take into account how a material changes on the atomic level when it is placed in a magnetic field with a certain moment. The moment that we are measuring with our magnetometer is the total moment of that sample.
\[ \chi \ =\ \frac{M}{H} \label{3} \]
where X = susceptibility, M = variation of magnetization, and H = applied field.
Magnetic Permeability
Magnetic permeability is the ability of a material to conduct an electric field. In the same way that materials conduct or resist electricity, materials also conduct or resist a magnetic flux or the flow of magnetic lines of force (Figure \(\PageIndex{6}\) ).
Ferromagnetic materials are usually highly permeable to magnetic fields. Just as electrical conductivity is defined as the ratio of the current density to the electric field strength, so the magnetic permeability, μ, of a particular material is defined as the ratio of flux density to magnetic field strength. However unlike in electrical conductivity magnetic permeability is nonlinear.
\[ \mu \ =\ B/H \label{4} \]
Permeability, where μ is written without a subscript, is known as absolute permeability. Instead a variant is used called relative permeability.
\[ \mu \ =\ \mu _{0} \times \mu _{r} \label{5} \]
Absolute permeability is a variation upon 'straight' or absolute permeability, μ, but is more useful as it makes clearer how the presence of a particular material affects the relationship between flux density and field strength. The term 'relative' arises because this permeability is defined in relation to the permeability of a vacuum, μ0.
\[ \mu _{r} \ =\ \mu / \mu_{0} \label{6} \]
For example, if you use a material for which μr = 3 then you know that the flux density will be three times as great as it would be if we just applied the same field strength to a vacuum.
Initial Permeability
Initial permeability describes the relative permeability of a material at low values of B (below 0.1 T). The maximum value for μ in a material is frequently a factor of between 2 and 5 or more above its initial value.
Low flux has the advantage that every ferrite can be measured at that density without risk of saturation. This consistency means that comparison between different ferrites is easy. Also, if you measure the inductance with a normal component bridge then you are doing so with respect to the initial permeability.
Permeability of a Vacuum in the SI
The permeability of a vacuum has a finite value - about 1.257 × 10-6 H m-1 - and is denoted by the symbol μ0. Note that this value is constant with field strength and temperature. Contrast this with the situation in ferromagnetic materials where μ is strongly dependent upon both. Also, for practical purposes, most non-ferromagnetic substances (such as wood, plastic, glass, bone, copper aluminum, air and water) have permeability almost equal to μ0; that is, their relative permeability is 1.0.
The permeability, μ, the variation of magnetic induction, with applied field,
\[ \mu \ =\ B/H \label{7} \]
Background Contributions
A single measurement of a sample's magnetization is relatively easy to obtain, especially with modern technology. Often it is simply a case of loading the sample into the magnetometer in the correct manner and performing a single measurement. This value is, however, the sum total of the sample, any substrate or backing and the sample mount. A sample substrate can produce a substantial contribution to the sample total.
For substrates that are diamagnetic, under zero applied field, this means it has no effect on the measurement of magnetization. Under applied fields its contribution is linear and temperature independent. The diamagnetic contribution can be calculated from knowledge of the volume and properties of the substrate and subtracted as a constant linear term to produce the signal from the sample alone. The diamagnetic background can also be seen clearly at high fields where the sample has reached saturation: the sample saturates but the linear background from the substrate continues to increase with field. The gradient of this background can be recorded and subtracted from the readings if the substrate properties are not known accurately.
Hysteresis
When a material exhibits hysteresis, it means that the material responds to a force and has a history of that force contained within it. Consider if you press on something until it depresses. When you release that pressure, if the material remains depressed and doesn’t spring back then it is said to exhibit some type of hysteresis. It remembers a history of what happened to it, and may exhibit that history in some way. Consider a piece of iron that is brought into a magnetic field, it retains some magnetization, even after the external magnetic field is removed. Once magnetized, the iron will stay magnetized indefinitely. To demagnetize the iron, it is necessary to apply a magnetic field in the opposite direction. This is the basis of memory in a hard disk drive.
The response of a material to an applied field and its magnetic hysteresis is an essential tool of magnetometry. Paramagnetic and diamagnetic materials can easily be recognized, soft and hard ferromagnetic materials give different types of hysteresis curves and from these curves values such as saturation magnetization, remnant magnetization and coercivity are readily observed. More detailed curves can give indications of the type of magnetic interactions within the sample.
Diamagnetism and Paramagnetizm
The intensity of magnetization depends upon both the magnetic moments in the sample and the way that they are oriented with respect to each other, known as the magnetic ordering.
Diamagnetic materials, which have no atomic magnetic moments, have no magnetization in zero field. When a field is applied a small, negative moment is induced on the diamagnetic atoms proportional to the applied field strength. As the field is reduced the induced moment is reduced.

In a paramagnet the atoms have a net magnetic moment but are oriented randomly throughout the sample due to thermal agitation, giving zero magnetization. As a field is applied the moments tend towards alignment along the field, giving a net magnetization which increases with applied field as the moments become more ordered. As the field is reduced the moments become disordered again by their thermal agitation. The figure shows the linear response M v H where μH << kT.
Ferromagnetism
The hysteresis curves for a ferromagnetic material are more complex than those for diamagnets or paramagnets. Below diagram shows the main features of such a curve for a simple ferromagnet.

In the virgin material (point 0) there is no magnetization. The process of magnetization, leading from point 0 to saturation at M = Ms, is outlined below. Although the material is ordered ferromagnetically it consists of a number of ordered domains arranged randomly giving no net magnetization. This is shown in below (a) with two domains whose individual saturation moments, Ms, lie antiparallel to each other.

As the magnetic field, H, is applied, (b), those domains which are more energetically favorable increase in size at the expense of those whose moment lies more antiparallel to H. There is now a net magnetization; M. Eventually a field is reached where all of the material is a single domain with a moment aligned parallel, or close to parallel, with H. The magnetization is now M = MsCosΘ where Θ is the angle between Ms along the easy magnetic axis and H. Finally Ms is rotated parallel to H and the ferromagnet is saturated with a magnetization M = Ms.
The process of domain wall motion affects the shape of the virgin curve. There are two qualitatively different modes of behavior known as nucleation and pinning, shown in Figure \(\PageIndex{10}\) as curves 1 and 2, respectively.
In a nucleation-type magnet saturation is reached quickly at a field much lower than the coercive field. This shows that the domain walls are easily moved and are not pinned significantly. Once the domain structure has been removed the formation of reversed domains becomes difficult, giving high coercivity. In a pinning-type magnet fields close to the coercive field are necessary to reach saturation magnetization. Here the domain walls are substantially pinned and this mechanism also gives high coercivity.
Remnance
As the applied field is reduced to 0 after the sample has reached saturation the sample can still possess a remnant magnetization, Mr. The magnitude of this remnant magnetization is a product of the saturation magnetization, the number and orientation of easy axes and the type of anisotropy symmetry. If the axis of anisotropy or magnetic easy axis is perfectly aligned with the field then Mr = Ms, and if perpendicular Mr= 0.
At saturation the angular distribution of domain magnetizations is closely aligned to H. As the field is removed they turn to the nearest easy magnetic axis. In a cubic crystal with a positive anisotropy constant, K1, the easy directions are <100>. At remnance the domain magnetizations will lie along one of the three <100> directions. The maximum deviation from H occurs when H is along the <111> axis, giving a cone of distribution of 55o around the axis. Averaging the saturation magnetization over this angle gives a remnant magnetization of 0.832 Ms.
Coercivity
The coercive field, Hc, is the field at which the remnant magnetization is reduced to zero. This can vary from a few Am for soft magnets to 107Am for hard magnets. It is the point of magnetization reversal in the sample, where the barrier between the two states of magnetization is reduced to zero by the applied field allowing the system to make a Barkhausen jump to a lower energy. It is a general indicator of the energy gradients in the sample which oppose large changes of magnetization.
The reversal of magnetization can come about as a rotation of the magnetization in a large volume or through the movement of domain walls under the pressure of the applied field. In general materials with few or no domains have a high coercivity whilst those with many domains have a low coercivity. However, domain wall pinning by physical defects such as vacancies, dislocations and grain boundaries can increase the coercivity.

The loop illustrated in Figure \(\PageIndex{10}\) is indicative of a simple bi-stable system. There are two energy minima: one with magnetization in the positive direction, and another in the negative direction. The depth of these minima is influenced by the material and its geometry and is a further parameter in the strength of the coercive field. Another is the angle, ΘH, between the anisotropy axis and the applied field. The above fig shows how the shape of the hysteresis loop and the magnitude of Hc varies with ΘH. This effect shows the importance of how samples with strong anisotropy are mounted in a magnetometer when comparing loops.
Temperature Dependence
A hysteresis curve gives information about a magnetic system by varying the applied field but important information can also be gleaned by varying the temperature. As well as indicating transition temperatures, all of the main groups of magnetic ordering have characteristic temperature/magnetization curves. These are summarized in Figure \(\PageIndex{11}\) and Figure \(\PageIndex{12}\).
At all temperatures a diamagnet displays only any magnetization induced by the applied field and a small, negative susceptibility.
The curve shown for a paramagnet (Figure \(\PageIndex{11}\) ) is for one obeying the Curie law,
\[ \chi \ =\ \frac{c}{t} \label{8} \]
and so intercepts the axis at T = 0. This is a subset of the Curie-Weiss law,
\[ \chi \ =\ \frac{C}{T- \Theta } \label{9} \]
where θ is a specific temperature for a particular substance (equal to 0 for paramagnets).
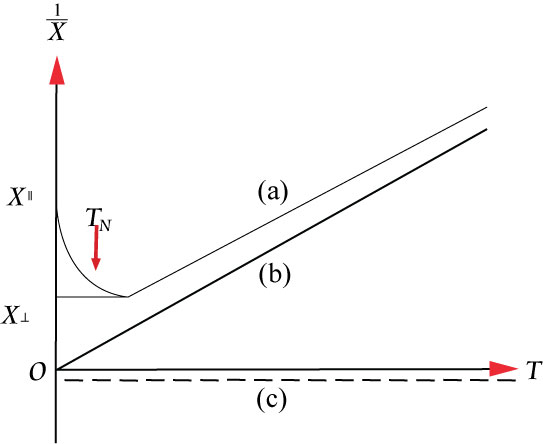

Above TN and TC both antiferromagnets and ferromagnets behave as paramagnets with 1/χ linearly proportional to temperature. They can be distinguished by their intercept on the temperature axis, T = Θ. Ferromagnetics have a large, positive Θ, indicative of their strong interactions. For paramagnetics Θ = 0 and antiferromagnetics have a negative Θ.
The net magnetic moment per atom can be calculated from the gradient of the straight line graph of 1/χ versus temperature for a paramagnetic ion, rearranging Curie's law to give \ref{10} .
\[ \mu \ = \sqrt{ \frac{3Ak}{N_{X} } } \label{10} \]
where A is the atomic mass, k is Boltzmann's constant, N is the number of atoms per unit volume and x is the gradient.
Ferromagnets below TC display spontaneous magnetization. Their susceptibility above TC in the paramagnetic region is given by the Curie-Weiss law
where g is the gyromagnetic constant. In the ferromagnetic phase with T greater than TC the magnetization M (T) can be simplified to a power law, for example the magnetization as a function of temperature can be given by \ref{11} .
\[ M(T) \approx (T_{C} \ -\ T) ^{\beta} \label{11} \]
where the term β is typically in the region of 0.33 for magnetic ordering in three dimensions.
The susceptibility of an antiferromagnet increases to a maximum at TN as temperature is reduced, then decreases again below TN. In the presence of crystal anisotropy in the system this change in susceptibility depends on the orientation of the spin axes: χ (parallel)decreases with temperature whilst χ (perpendicular) is constant. These can be expressed as \ref{12} .
\[ \chi \perp = \frac{C}{2 \Theta} \label{12} \]
where C is the Curie constant and Θ is the total change in angle of the two sublattice magnetizations away from the spin axis, and \ref{13}
\[ \chi \parallel \ =\ \frac{2n_{g} \mu ^{2} _{H} B'(J,a' _{0} ) }{2kT\ +\ n_{g} \mu ^{2} _{H} \gamma \rho B'(J,a' _{0}) } \perp \ = \frac{C}{2 \Theta} \label{13} \]
where ng is the number of magnetic atoms per gramme, B’ is the derivative of the Brillouin function with respect to its argument a’, evaluated at a’0, μH is the magnetic moment per atom and γ is the molecular field coefficient.
Theory of a Superconducting Quantum Interference Device (SQUID)
One of the most sensitive forms of magnetometry is SQUID magnetometry. This uses technique uses a combination of superconducting materials and Josephson junctions to measure magnetic fields with resolutions up to ~10-14 kG or greater. In the proceeding pages we will describe how a SQUID actually works.
Electron-pair Waves
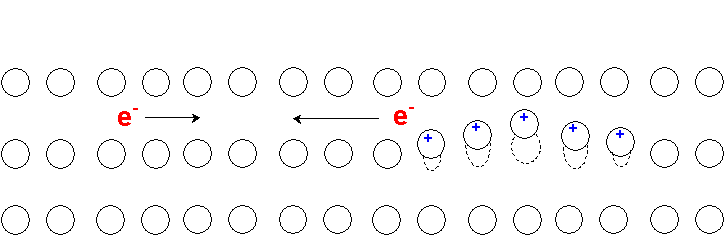
In superconductors the resistanceless current is carried by pairs of electrons, known as Cooper Pairs. A Cooper Pair is a pair of electrons. Each electron has a quantized wavelength. With a Cooper pair each electrons wave couples with its opposite number over a large distances. This phenomenon is a result of the very low temperatures at which many materials will superconduct.
What exactly is superconductance? When a material is at very low temperatures, its crystal lattice behaves differently than when it higher temperatures. Usually at higher temperatures a material will have large vibrations called in the crystal lattice. These vibrations scatter electrons as they pass through this lattice (Figure \(\PageIndex{13}\) ), and this is the basis for bad conductance.

With a superconductor the material is designed to have very small vibrations, these vibrations are lessened even more by cooling the material to extremely low temperatures. With no vibrations there is no scattering of the electrons and this allows the material to superconduct.
The origin of a Cooper pair is that as the electron passes through a crystal lattice at superconducting temperatures it negative charge pulls on the positive charge of the nuclei in the lattice through coulombic interactions producing a ripple. An electron traveling in the opposite direction is attracted by this ripple. This is the origin of the coupling in a Cooper pair (Figure \(\PageIndex{14}\) ).
A passing electron attracts the lattice, causing a slight ripple toward its path. Another electron passing in the opposite direction is attracted to that displacement (Figure \(\PageIndex{15}\) ).


Each pair can be treated as a single particle with a whole spin, not half a spin such as is usually the case with electrons. This is important, as an electron which is classed in a group of matter called Fermions are governed by the Fermi exclusion principle which states that anything with a spin of one half cannot occupy the same space as something with the same spin of one half. This turns the electron means that a Cooper pair is in fact a Boson the opposite of a Fermion and this allows the Coopers pairs to condensate into one wave packet. Each Coopers pair has a mass and charge twice that of a single electron, whose velocity is that of the center of mass of the pair. This coupling can only happen in extremely cold conditions as thermal vibrations become greater than the force that an electron can exert on a lattice. And thus scattering occurs.
Each pair can be represented by a wavefunction of the form
where P is the net momentum of the pair whose center of mass is at r. However, all the Cooper pairs in a superconductor can be described by a single wavefunction yet again due to the fact that the electrons are in a Coopers pair state and are thus Bosons in the absence of a current because all the pairs have the same phase - they are said to be "phase coherent"
This electron-pair wave retains its phase coherence over long distances, and essentially produces a standing wave over the device circuit. In a SQUID there are two paths which form a circle and are made with the same standing wave (Figure \(\PageIndex{17}\) ). The wave is split in two sent off along different paths, and then recombined to record an interference pattern by adding the difference between the two.

This allows measurement at any phase differences between the two components, which if there is no interference will be exactly the same, but if there is a difference in their path lengths or in some interaction that the waves encounters such as a magnetic field it will correspond in a phase difference at the end of each path length.
A good example to use is of two water waves emanating from the same point. They will stay in phase if they travel the same distance, but will fall out of phase if one of them has to deviate around an obstruction such as a rock. Measuring the phase difference between the two waves then provides information about the obstruction.
Phase and Coherence
Another implication of this long range coherence is the ability to calculate phase and amplitude at any point on the wave's path from the knowledge of its phase and amplitude at any single point, combined with its wavelength and frequency. The wavefunction of the electron-pair wave in the above eqn. can be rewritten in the form of a one-dimensional wave as
\[ \psi_{p} \ =\ \psi \ sin(2 \pi ) (\frac{ \chi }{ \lambda } \ - \nu t ) \label{14} \]
If we take the wave frequency, V, as being related to the kinetic energy of the Cooper pair with a wavelength, λ, being related to the momentum of the pair by the relation λ = h/p then it is possible to evaluate the phase difference between two points in a current carrying superconductor.
If a resistanceless current flows between points X and Y on a superconductor there will be a phase difference between these points that is constant in time.
Effect of a Magnetic Field
The parameters of a standing wave are dependent on a current passing through the circuit; they are also strongly affected by an applied magnetic field. In the presence of a magnetic field the momentum, p, of a particle with charge q in the presence of a magnetic field becomes mV + qA where A is the magnetic vector potential. For electron-pairs in an applied field their moment P is now equal to 2mV+2eA.
In an applied magnetic field the phase difference between points X and Y is now a combination of that due to the supercurrent and that due to the applied field.
The Fluxoid
One effect of the long range phase coherence is the quantization of magnetic flux in a superconducting ring. This can either be a ring, or a superconductor surrounding a non-superconducting region. Such an arrangement can be seen in Figure \(\PageIndex{18}\) where region N has a flux density B within it due to supercurrents flowing around it in the superconducting region S.

In the closed path XYZ encircling the non-superconducting region there will be a phase difference of the electron-pair wave between any two points, such as X and Y, on the curve due to the field and the circulating current.
If the superelectrons are represented by a single wave then at any point on XYZX it can only have one value of phase and amplitude. Due to the long range coherence the phase is single valued also called quantized meaning around the circumference of the ring Δφ must equal 2πn where n is any integer. Due to the wave only having a single value the fluxoid can only exist in quantized units. This quantum is termed the fluxon, φ0, given by \ref{15} .
\[ \Phi_{0} = \dfrac{h}{2e} = 2.07 \times 10^{-15} W b \label{15} \]
Josephson Tunneling
If two superconducting regions are kept totally isolated from each other the phases of the electron-pairs in the two regions will be unrelated. If the two regions are brought together then as they come close electron-pairs will be able to tunnel across the gap and the two electron-pair waves will become coupled. As the separation decreases, the strength of the coupling increases. The tunneling of the electron-pairs across the gap carries with it a superconducting current as predicted by B.D. Josephson and is called "Josephson tunneling" with the junction between the two superconductors called a "Josephson junction" (Figure \(\PageIndex{16}\) ).
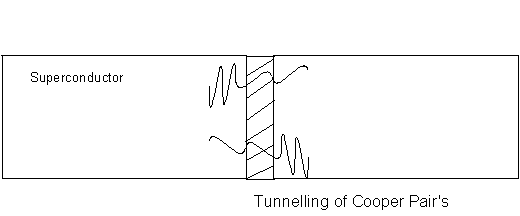
The Josephson tunneling junction is a special case of a more general type of weak link between two superconductors. Other forms include constrictions and point contacts but the general form is of a region between two superconductors which has a much lower critical current and through which a magnetic field can penetrate.
Superconducting Quantum Interference Device (SQUID)
A superconducting quantum interference device (SQUID) uses the properties of electron-pair wave coherence and Josephson Junctions to detect very small magnetic fields. The central element of a SQUID is a ring of superconducting material with one or more weak links called Josephesons Junctions. An example is shown in the below. With weak-links at points W and X whose critical current, ic, is much less than the critical current of the main ring. This produces a very low current density making the momentum of the electron-pairs small. The wavelength of the electron-pairs is thus very long leading to little difference in phase between any parts of the ring.
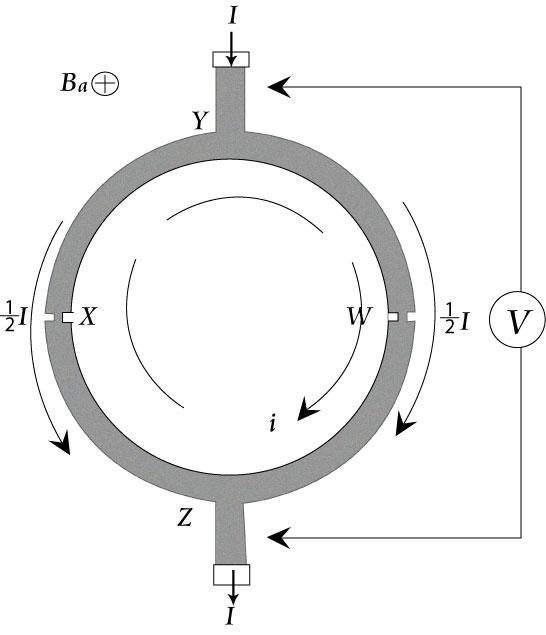
If a magnetic field, Ba , is applied perpendicular to the plane of the ring (Figure \(\PageIndex{21}\), a phase difference is produced in the electron-pair wave along the path XYW and WZX. One of the features of a superconducting loop is that the magnetic flux, Φ, passing through it which is the product of the magnetic field and the area of the loop and is quantized in units of Φ0 = h/ (2e), where h is Planck’s constant, 2e is the charge of the Cooper pair of electrons, and Φ0 has a value of 2 × 10–15 tesla m2. If there are no obstacles in the loop, then the superconducting current will compensate for the presence of an arbitrary magnetic field so that the total flux through the loop (due to the external field plus the field generated by the current) is a multiple of Φ0.

Josephson predicted that a superconducting current can be sustained in the loop, even if its path is interrupted by an insulating barrier or a normal metal. The SQUID has two such barriers or ‘Josephson junctions’. Both junctions introduce the same phase difference when the magnetic flux through the loop is 0, Φ0, 2Φ0 and so on, which results in constructive interference, and they introduce opposite phase difference when the flux is Φ0/2, 3Φ0/2 and so on, which leads to destructive interference. This interference causes the critical current density, which is the maximum current that the device can carry without dissipation, to vary. The critical current is so sensitive to the magnetic flux through the superconducting loop that even tiny magnetic moments can be measured. The critical current is usually obtained by measuring the voltage drop across the junction as a function of the total current through the device. Commercial SQUIDs transform the modulation in the critical current to a voltage modulation, which is much easier to measure.
An applied magnetic field produces a phase change around a ring, which in this case is equal
\[ \Delta \Phi (B) \ =\ 2 \pi \frac{ \Phi _{a} }{ \Phi _{0} } \label{16} \]
where Φa is the flux produced in the ring by the applied magnetic field. The magnitude of the critical measuring current is dependent upon the critical current of the weak-links and the limit of the phase change around the ring being an integral multiple of 2π. For the whole ring to be superconducting the following condition must be met
\[ \alpha \ +\ \beta \ +\ 2 \pi \frac{ \Phi _{a} }{ \Phi _{0} } \label{17} \]
where α and β are the phase changes produced by currents across the weak-links and 2πΦa/Φo is the phase change due to the applied magnetic field.
When the measuring current is applied α and β are no longer equal, although their sum must remain constant. The phase changes can be written as \ref{18}
\[ \alpha = \pi [ n - \frac{ \Phi _{a} }{ \Phi _{0} } ] \ -\ \delta \beta \ = \ \pi \ [n \ - \frac{ \Phi _{a} }{ \Phi _{0} } ] + \delta \label{18} \]
where δ is related to the measuring current I. Using the relation between current and phase from the above Eqn. and rearranging to eliminate i we obtain an expression for I, \ref{19}
\[ I_{c} \ =\ 2i_{c} | cos \pi \frac{ \Phi _{a} }{ \Phi _{0} } , sin \delta | \label{19} \]
As sinδ cannot be greater than unity we can obtain the critical measuring current, Ic from the above \ref{20}
\[ I_{c} \ =\ 2i_{c} | cos \pi \frac{ \Phi _{a} }{ \Phi _{0} } | \label{20} \]
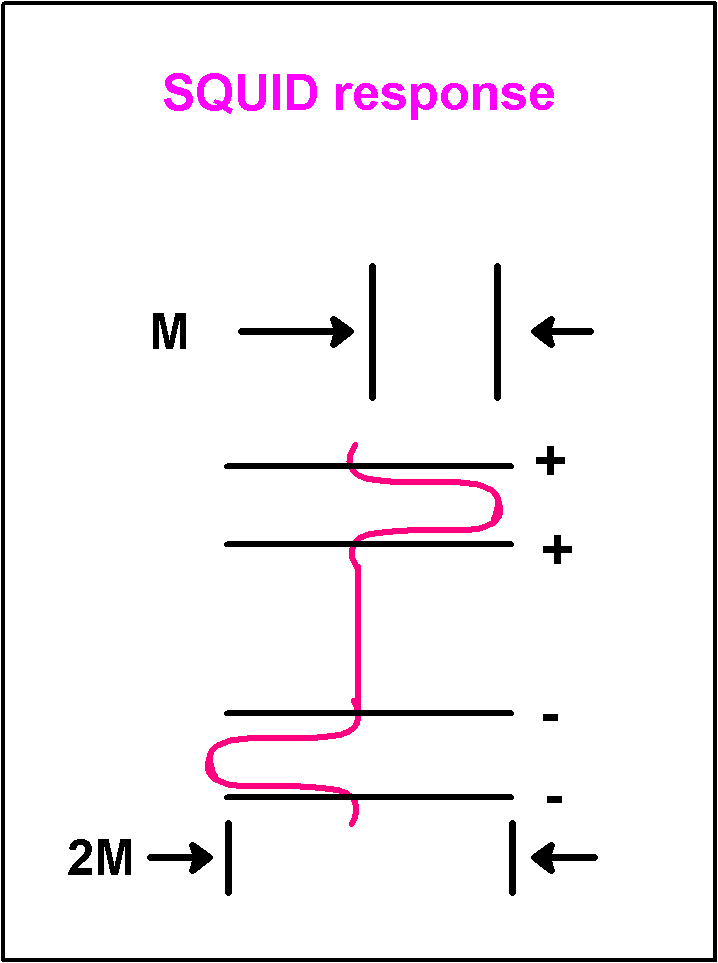
which gives a periodic dependence on the magnitude of the magnetic field, with a maximum when this field is an integer number of fluxons and a minimum at half integer values as shown in the below figure.

Practical Guide to Using a Superconducting Quantum Interference Device
SQUIDs offer the ability to measure at sensitivities unachievable by other magnetic sensing methodologies. However, their sensitivity requires proper attention to cryogenics and environmental noise. SQUIDs should only be used when no other sensor is adequate for the task. There are many exotic uses for SQUID however we are just concerned with the laboratory applications of SQUID.
In most physical and chemical laboratories a device called a MPMS (Figure \(\PageIndex{23}\) )
is used to measure the magnetic moment of a sample by reading the output of the SQUID detector. In a MPMS the sample moves upward through the electronic pick up coils called gradiometers. One upward movement is one whole scan. Multiple scans are used and added together to improve measurement resolution. After collecting the raw voltages, there is computation of the magnetic moments of the sample.
The MPMS measures the moment of a sample by moving it through a liquid Helium cooled, superconducting sensing coil. Many different measurements can be carried out using an MPMS however we will discuss just a few.

Using an Magnetic Property Measurement System (MPMS)
DC Magentization
DC magnetization is the magnetic per unit volume (M) of a sample. If the sample doesn’t have a permanent magnetic moment, a field is applied to induce one. The sample is then stepped through a superconducting detection array and the SQUID’s output voltage is processed and the sample moment computed. Systems can be configured to measure hysteresis loops, relaxation times, magnetic field, and temperature dependence of the magnetic moment.
A DC field can be used to magnetize samples. Typically, the field is fixed and the sample is moved into the detection coil’s region of sensitivity. The change in detected magnetization is directly proportional to the magnetic moment of the sample. Commonly referred to as SQUID magnetometers, these systems are properly called SQUID susceptometers (Figure \(\PageIndex{24}\) ).
They have a homogeneous superconducting magnet to create a very uniform field over the entire sample measuring region and the superconducting pickup loops. The magnet induces a moment allowing a measurement of magnetic susceptibility. The superconducting detection loop array is rigidly mounted in the center of the magnet. This array is configured as a gradient coil to reject external noise sources. The detection coil geometry determines what mathematical algorithm is used to calculate the net magnetization.
An important feature of SQUIDs is that the induced current is independent of the rate of flux change. This provides uniform response at all frequencies i.e., true dc response and allows the sample to be moved slowly without degrading performance. As the sample passes through a coil, it changes the flux in that coil by an amount proportional to the magnetic moment M of the sample. The peak-to-peak signal from a complete cycle is thus proportional to twice M. The SQUID sensor shielded inside a niobium can is located where the fringe fields generated by the magnet are less than 10 mT. The detection coil circuitry is typically constructed using NbTi (Figure \(\PageIndex{25}\) ). This allows measurements in applied fields of 9 T while maintaining sensitivities of 10−8 emu. Thermal insulation not shown is placed between the detection coils and the sample tube to allow the sample temperature to be varied.

The use of a variable temperature insert can allow measurements to be made over a wide range 1.8–400 K. Typically, the sample temperature is controlled by helium gas flowing slowly past the sample. The temperature of this gas is regulated using a heater located below the sample measuring region and a thermometer located above the sample region. This arrangement ensures that the entire region has reached thermal equilibrium prior to data acquisition. The helium gas is obtained from normal evaporation in the Dewar, and its flow rate is controlled by a precision regulating valve.
Procedures when using an MPMS
Calibration
The magnetic moment calibration for the SQUID is determined by measuring a palladium standard over a range of magnetic fields and then by adjusting to obtain the correct moment for the standard. The palladium standard samples are effectively point sources with an accuracy of approximately 0.1%.
Sample mounting considerations
The type, size and geometry of a sample is usually sufficient to determine the method you use to attach it to the sample. However mostly for MPMS measurements a plastic straw is used. This is due to the straw having minimal magnetic susceptibility.
However there are a few important considerations for the sample holder design when mounting a sample for measurement in a magnetometer. The sample holder can be a major contributor to the background signal. Its contribution can be minimized by choosing materials with low magnetic susceptibility and by keeping the mass to a minimum such as a plastic straw mentioned above.
The materials used to hold a sample must perform well over the temperature range to be used. In a MPMS, the geometric arrangement of the background and sample is critical when their magnetic susceptibilities will be of similar magnitude. Thus, the sample holder should optimize the sample’s positioning in the magnetometer. A sample should be mounted rigidly in order to avoid excess sample motion during measurement. A sample holder should also allow easy access for mounting the sample, and its background contribution should be easy to measure. This advisory introduces some mounting methods and discusses some of the more important considerations when mounting samples for the MPMS magnetometer. Keep in mind that these are only recommendations, not guaranteed procedures. The researcher is responsible for assuring that the methods and materials used will meet experimental requirements.
Sample Mounts
Platform Mounting
For many types of samples, mounting to a platform is the most convenient method. The platform’s mass and susceptibility should be as small as possible in order to minimize its background contribution and signal distortion.
Plastic Disc
A plastic disc about 2 mm thick with an outside diameter equivalent to the pliable plastic tube’s diameter (a clear drinking straw is suitable) is inserted and twisted into place. The platform should be fairly rigid. Mount samples onto this platform with glue. Place a second disc, with a diameter slightly less than the inside diameter of the tube and with the same mass, on top of the sample to help provide the desired symmetry. Pour powdered samples onto the platform and place a second disc on top. The powders will be able to align with the field. Make sure the sample tube is capped and ventilated.
Crossed Threads
Make one of the lowest mass sample platforms by threading a cross of white cotton thread (colored dyes can be magnetic). Using a needle made of a nonmagneticmetal, or at least carefully cleaned, thread some white cotton sewingthread through the tube walls and tie a secure knot so that the thread platform isrigid. Glue a sample to this platform or use the platform as asupport for a sample in a container. Use an additional thread cross on top to holdthe container in place.
Gelatin Capsule
Gelatin capsules can be very useful for containing and mounting samples. Many aspects of using gelatin capsules have been mentioned in the section, Containing the Sample. It is best if the sample is mounted near the capsule’s center, or if it completely fills the capsule. Use extra capsule parts to produce mirror symmetry. The thread cross is an excellent way of holding a capsule in place.
Thread Mounting
Another method of sample mounting is attaching the sample to a thread that runs through the sample tube. The thread can be attached to the sample holder at the ends of the sample tube with tape, for example. This method can be very useful with flat samples, such as those on substrates, particularly when the field is in the plane of the film. Be sure to close the sample tube with caps.
- Mounting with a disc platform.
- Mounting on crossed threads.
- Long thread mounting.
Steps for Inserting the Sample
- Cut off a small section of a clear plastic drinking straw. The section must be small enough to fit inside the straw.
- Weigh and measure the sample.
- Use plastic tweezers to place the sample inside the small straw segment. It is important to use plastic tweezers not metallic ones as these will contaminate the sample.
- Place the small straw segment inside the larger one. It should be approximately in the middle of the large drinking straw.
- Attach the straw to the sample rod which is used to insert the sample into the SQUID machine.
- Insert the sample rod with the attached straw into the vertical insertion hole on top of the SQUID.
Center the Sample
The sample must be centered in the SQUID pickup coils to ensure that all coils sense the magnetic moment of the sample. If the sample is not centered, the coils read only part of the magnetic moment.
During a centering measurement the MPMS scans the entire length of the samples vertical travel path, and the MPMS reads the maximum number of data points. During centering there are a number of terms which need to be understood.
- A scan length is the length of a scan of a particular sample which should usually try and be the maximum of the sample.
- A sample is centered when it is in the middle of a scan length. The data points are individual voltage readings plotting response curves in centering scan data files.
- Autotracking is the adjustment of a sample position to keep a sample centered in SQUID coils. Autotracking compensates for thermal expansion and contraction in a sample rod.
As soon as a centering measurement is initiated, the sample transport moves upward, carrying the sample through the pickup coils. While the sample moves through the coils, the MPMS measures the SQUID’s response to the magnetic moment of the sample and saves all the data from the centering measurement.
After a centering plot is performed the plot is examined to determine whether the sample is centered in the SQUID pickup coils. The sample is centered when the part of the large, middle curve is within 5cm of the half-way point of the scan length.
The shape of the plot is a function of the geometry of the coils. The coils are wound in a way which strongly rejects interference from nearby magnetic sources and lets the MPMS function without a superconducting shield around the pickup coils.
Geometric Considerations
To minimize background noise and stray field effects, the MPMS magnetometer pick-up coil takes the form of a second-order gradiometer. An important feature of this gradiometer is that moving a long, homogeneous sample through it produces no signal as long as the sample extends well beyond the ends of the coil during measurement.
As a sample holder is moved through the gradiometer pickup coil, changes in thickness, mass, density, or magnetic susceptibility produce a signal. Ideally, only the sample to be measured produces this change. A homogeneous sample that extends well beyond the pick-up coils does not produce a signal, yet a small sample does produce a signal. There must be a crossover between these two limits. The sample length (along the field direction) should not exceed 10 mm. In order to obtain the most accurate measurements, it is important to keep the sample susceptibility constant over its length; otherwise distortions in the SQUID signal (deviations from a dipole signal) can result. It is also important to keep the sample close to the magnetometer centerline to get the most accurate measurements. When the sample holder background contribution is similar in magnitude to the sample signal, the relative positions of the sample and the materials producing the background are important. If there is a spatial offset between the two along the magnet axis, the signal produced by the combined sample and background can be highly distorted and will not be characteristic of the dipole moment being measured.
Even if the signal looks good at one temperature, a problem can occur if either of the contributions are temperature dependent.
Careful sample positioning and a sample holder with a center, or plane, of symmetry at the sample (i.e. materials distributed symmetrically about the sample, or along the principal axis for a symmetry plane) helps eliminate problems associated with spatial offsets.
Containing the Sample
Keep the sample space of the MPMS magnetometer clean and free of contamination with foreign materials. Avoid accidental sample loss into the sample space by properly containing the sample in an appropriate sample holder. In all cases it is important to close the sample holder tube with caps in order to contain a sample that might become unmounted. This helps avoid sample loss and subsequent damage during the otherwise unnecessary recovery procedure. Position caps well out of the sample-measuring region and introduce proper venting.
Sample Preparation Workspace
Work area cleanliness and avoiding sample contamination are very important concerns. There are many possible sources of contamination in a laboratory. Use diamond tools when cutting hard materials. Avoid carbide tools because of potential contamination by the cobalt binder found in many carbide materials. The best tools for preparing samples and sample holders are made of plastic, titanium, brass, and beryllium copper (which also has a small amount of cobalt). Tools labeled non-magnetic can actually be made of steel and often be made "magnetic" from exposure to magnetic fields. However, the main concern from these "non-magnetic" tools is contamination by the iron and other ferrous metals in the tool. It is important to have a clean white-papered workspace and a set of tools dedicated to mounting your own samples. In many cases, the materials and tools used can be washed in dilute acid to remove ferrous metal impurities. Follow any acid washes with careful rinsing with deionized water.
Powdered samples pose a special contamination threat, and special precautions must be taken to contain them. If the sample is highly magnetic, it is often advantageous to embed it in a low susceptibility epoxy matrix like Duco cement. This is usually done by mixing a small amount of diluted glue with the powder in a suitable container such as a gelatin capsule. Potting the sample in this way can keep the sample from shifting or aligning with the magnetic field. In the case of weaker magnetic samples, measure the mass of the glue after drying and making a background measurement. If the powdered sample is not potted, seal it into a container, and watch it carefully as it is cycled in the airlock chamber.
Pressure Equalization
The sample space of the MPMS has a helium atmosphere maintained at low pressure of a few torr. An airlock chamber is provided to avoid contamination of the sample space with air when introducing samples into the sample space. By pushing the purge button, the airlock is cycled between vacuum and helium gas three times, then pumped down to its working pressure. During the cycling, it is possible for samples to be displaced in their holders, sealed capsules to explode, and sample holders to be deformed. Many of these problems can be avoided if the sample holder is properly ventilated. This requires placing holes in the sample holder, out of the measuring region that will allow any closed spaces to be opened to the interlock chamber.
Air-sensitive Samples and Liquid Samples
When working with highly air-sensitive samples or liquid samples it is best to first seal the sample into a glass tube. NMR and EPR tubes make good sample holders since they are usually made of a high-quality, low-susceptibility glass or fused silica. When the sample has a high susceptibility, the tube with the sample can be placed onto a platform like those described earlier. When dealing with a low susceptibility sample, it is useful to rest the bottom of the sample tube on a length of the same type of glass tubing. By producing near mirror symmetry, this method gives a nearly constant background with position and provides an easy method for background measurement (i.e., measure the empty tube first, then measure with a sample). Be sure that the tube ends are well out of the measuring region.
When going to low temperatures, check to make sure that the sample tube will not break due to differential thermal expansion. Samples that will go above room temperature should be sealed with a reduced pressure in the tube and be checked by taking the sample to the maximum experimental temperature prior to loading it into the magnetometer. These checks are especially important when the sample may be corrosive, reactive, or valuable.
Oxygen Contamination
This application note describes potential sources for oxygen contamination in the sample chamber and discusses its possible effects. Molecular oxygen, which undergoes an antiferromagnetic transition at about 43 K, is strongly paramagnetic above this temperature. The MPMS system can easily detect the presence of a small amount of condensed oxygen on the sample, which when in the sample chamber can interfere significantly with sensitive magnetic measurements. Oxygen contamination in the sample chamber is usually the result of leaks in the system due to faulty seals, improper operation of the airlock valve, outgassing from the sample, or cold samples being loaded.


