16.2: Propagation of Uncertainty
- Page ID
- 127256
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In Chapter 4 we considered the basic mathematical details of a propagation of uncertainty, limiting our treatment to the propagation of measurement error. This treatment is incomplete because it omits other sources of uncertainty that contribute to the overall uncertainty in our results. Consider, for example, Exercise 4.3.1, in which we determined the uncertainty in a standard solution of Cu2+ prepared by dissolving a known mass of Cu wire with HNO3, diluting to volume in a 500-mL volumetric flask, and then diluting a 1-mL portion of this stock solution to volume in a 250-mL volumetric flask. To calculate the overall uncertainty we included the uncertainty in weighing the sample and the uncertainty in using the volumetric glassware. We did not consider other sources of uncertainty, including the purity of the Cu wire, the effect of temperature on the volumetric glassware, and the repeatability of our measurements. In this appendix we take a more detailed look at the propagation of uncertainty, using the standardization of NaOH as an example.
Standardizing a Solution of NaOH
Because solid NaOH is an impure material, we cannot directly prepare a stock solution by weighing a sample of NaOH and diluting to volume. Instead, we determine the solution’s concentration through a process called a standardization. A fairly typical procedure is to use the NaOH solution to titrate a carefully weighed sample of previously dried potassium hydrogen phthalate, C8H5O4K, which we will write here, in shorthand notation, as KHP. For example, after preparing a nominally 0.1 M solution of NaOH, we place an accurately weighed 0.4-g sample of dried KHP in the reaction vessel of an automated titrator and dissolve it in approximately 50 mL of water (the exact amount of water is not important). The automated titrator adds the NaOH to the KHP solution and records the pH as a function of the volume of NaOH. The resulting titration curve provides us with the volume of NaOH needed to reach the titration's endpoint.
The example below is adapted from Ellison, S. L. R.; Rosslein, M.; Williams, A. EURACHEM/CITAC Guide: Quantifying Uncertainty in Analytical Measurement, 3nd Edition, 2012. See Chapter 5 for further details about standardizations and see Chapter 9 for further details about titrations
The end point of the titration is the volume of NaOH that corresponds to the stoichiometric reaction between NaOH and KHP.
\[\ce{NaOH}(aq) + \ce{C8H5O4K}(aq) \ce{->} \ce{C8H4O4^{2-}}(aq) + \ce{K+}(aq) + \ce{Na+}(aq) + \ce{H2O}(l) \nonumber\]
Knowing the mass of KHP and the volume of NaOH needed to reach the endpoint, we use the following equation to calculate the molarity of the NaOH solution.
\[C_\ce{NaOH} = \frac {1000 \times m_\ce{KHP} \times P_\ce{KHP}} {FW_\ce{KHP} \times V_\ce{NaOH}} \nonumber\]
where CNaOH is the concentration of NaOH (in mol KHP/L), mKHP is the mass of KHP taken (in g), PKHP is the purity of the KHP (where PKHP = 1 means the KHP is pure and has no impurities), FWKHP is the molar mass of KHP (in g KHP/mol KHP), and VNaOH is the volume of NaOH (in mL). The factor of 1000 simply converts the volume in mL to L.
Identifying and Analyzing Sources of Uncertainty
Although it seems straightforward, identifying sources of uncertainty requires care as it easy to overlook important sources of uncertainty. One approach is to use a cause-and-effect diagram, also known as an Ishikawa diagram—named for its inventor, Kaoru Ishikawa—or a fish bone diagram. To construct a cause-and-effect diagram, we first draw an arrow that points to the desired result; this is the diagram's trunk. We then add five main branch lines to the trunk, one for each of the four parameters that determine the concentration of NaOH (mKHP, PKHP, FWKHP, and VNaOH) and one for the method's repeatability, R. Next we add additional branches to the main branch for each of these five factors, continuing until we account for all potential sources of uncertainty. Figure 16.2.1 shows the complete cause-and-effect diagram for this analysis.
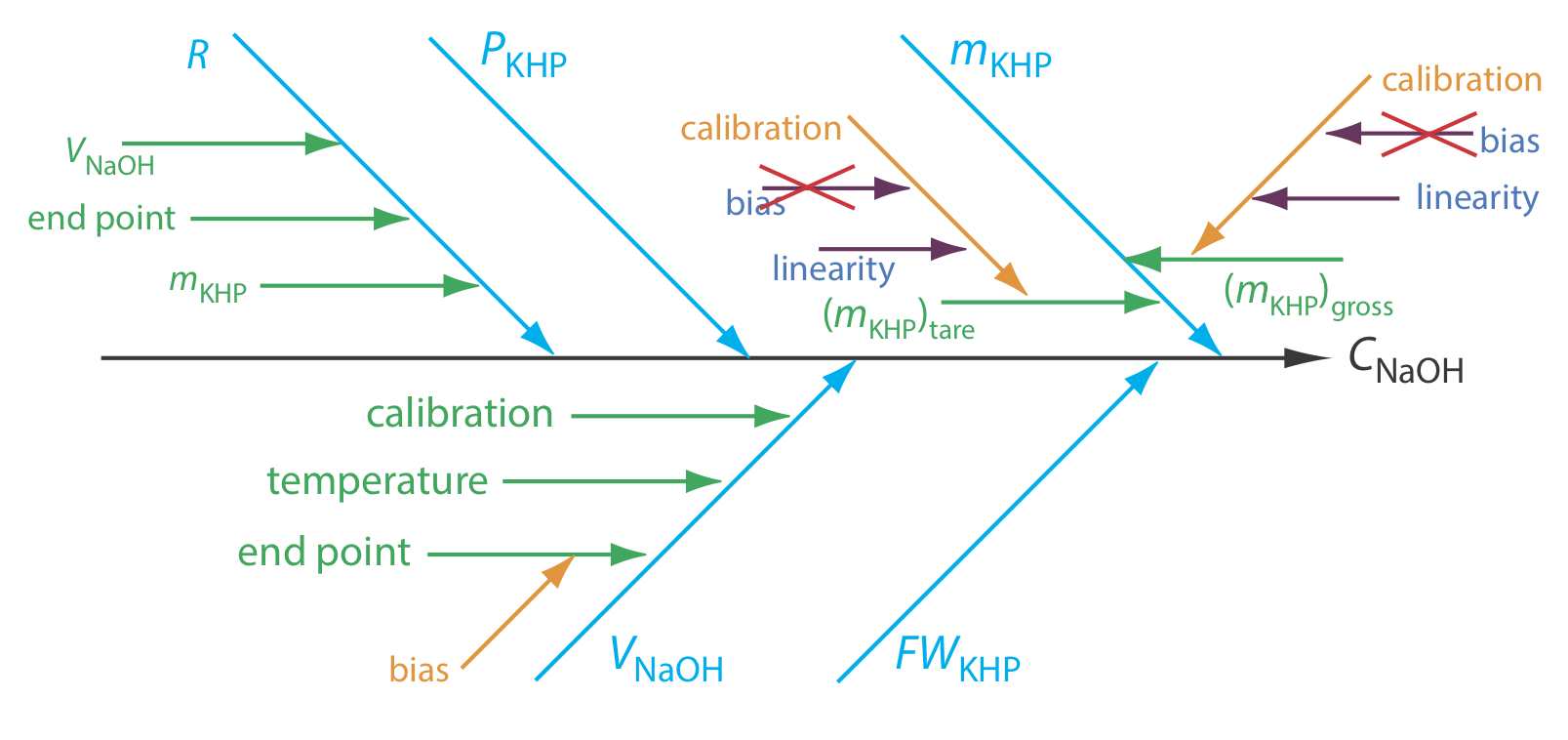
Before we continue, let's take a closer look at Figure 16.2.1 to make sure that we understand each branch of the diagram. To determine the mass of KHP, mKHP, we make two measurements: taring the balance and weighing the gross sample. Each of these measurements is subject to a calibration uncertainty. When we calibrate a balance, we essentially are creating a calibration curve of the balance's signal as a function of mass. Any calibration curve is subject to an uncertainty in the y-intercept (bias) and an uncertainty in the slope (linearity). We can ignore the calibration bias because it contributes equally to both (mKHP)gross and (mKHP)tare, and because we determine the mass of KHP by difference.
\[m_\ce{KHP} = \left( m_\ce{KHP} \right)_\text{gross} - \left( m_\ce{KHP} \right)_\text{tare} \nonumber\]
The volume of NaOH, VNaOH, at the end point has three sources of uncertainty. First, an automated titrator uses a piston to deliver NaOH to the reaction vessel, which means the volume of NaOH is subject to an uncertainty in the piston's calibration. Second, because a solution’s volume varies with temperature, there is an additional source of uncertainty due to any fluctuation in the ambient temperature during the analysis. Finally, there is a bias in the titration’s end point if the NaOH reacts with any species other than the KHP.
Repeatability, R, is a measure of how consistently we can repeat the analysis. Each instrument we use—the balance and the automated titrator—contributes to this uncertainty. In addition, our ability to consistently detect the end point also contributes to repeatability. Finally, there are no secondary factors that affect the uncertainty of the KHP's purity, PKHP, or its molar mass, FWKHP.
Estimating the Standard Deviation for Measurements
To complete a propagation of uncertainty we must express each measurement’s uncertainty in the same way, usually as a standard deviation. Measuring the standard deviation for each measurement requires time and is not always practical. Fortunately, most manufacture provides a tolerance range for glassware and instruments. A 100-mL volumetric glassware, for example, has a tolerance of \(\pm 0.1 \text{ mL}\) at a temperature of 20 oC. We can convert a tolerance range to a standard deviation using one of the following three approaches.
Assume a Uniform Distribution
Figure 16.2.2 a shows a uniform distribution between the limits of \(\pm x\), in which each result between the limits is equally likely. A uniform distribution is the choice when the manufacturer provides a tolerance range without specifying a level of confidence and when there is no reason to believe that results near the center of the range are more likely than results at the ends of the range. For a uniform distribution the estimated standard deviation, s, is
\[s = \frac {x} {\sqrt{3}} \nonumber\]
This is the most conservative estimate of uncertainty as it gives the largest estimate for the standard deviation.

Assume a Triangular Distribution
Figure 16.2.2 b shows a triangular distribution between the limits of \(\pm x\), in which the most likely result is at the center of the distribution, decreasing linearly toward each limit. A triangular distribution is the choice when the manufacturer provides a tolerance range without specifying a level of confidence and when there is a good reason to believe that results near the center of the range are more likely than results at the ends of the range. For a triangular distribution the estimated standard deviation, s, is
\[s = \frac {x} {\sqrt{6}} \nonumber\]
This is a less conservative estimate of uncertainty as, for any value of x, the standard deviation is smaller than that for a uniform distribution.
Assume a Normal Distribution
Figure 16.2.2 c shows a normal distribution that extends, as it must, beyond the limits of \(\pm x\), and which is centered at the mid-point between –x and +x. A normal distribution is the choice when we know the confidence interval for the range. For a normal distribution the estimated standard deviation, s, is
\[s = \frac {x} {z} \nonumber\]
where z is 1.96 for a 95% confidence interval and 3.00 for a 99.7% confidence interval.
Completing the Propagation of Uncertainty
Now we are ready to return to our example and determine the uncertainty for the standardization of NaOH. First we establish the uncertainty for each of the five primary sources—the mass of KHP, the volume of NaOH at the end point, the purity of the KHP, the molar mass for KHP, and the titration’s repeatability. Having established these, we can combine them to arrive at the final uncertainty.
Uncertainty in the Mass of KHP
After drying the KHP, we store it in a sealed container to prevent it from readsorbing moisture. To find the mass of KHP we first weigh the container, obtaining a value of 60.5450 g, and then weigh the container after removing a portion of KHP, obtaining a value of 60.1562 g. The mass of KHP, therefore, is 60.5450 – 60.1562 = 0.3888 g, or 388.8 mg.
To find the uncertainty in this mass we examine the balance’s calibration certificate, which indicates that its tolerance for linearity is \(\pm 0.15 \text{ mg}\). We will assume a uniform distribution because there is no reason to believe that any result within this range is more likely than any other result. Our estimate of the uncertainty for any single measurement of mass, u(m), is
\[u(m) = \frac {0.15 \text{ mg}} {\sqrt{3}} = \pm 0.087 \text{ mg} \nonumber\]
Because we determine the mass of KHP by subtracting the container’s final mass from its initial mass, the uncertainty in the mass of KHP u(mKHP), is given by the following propagation of uncertainty.
\[u(m_{\text{KHP}}) = \sqrt{\left( 0.087 \text{ mg} \right)^2 + \left( 0.087 \text{ mg} \right)^2} =\pm 0.12 \text{ mg} \nonumber\]
Uncertainty in the Volume of NaOH
After we place the sample of KHP in the automated titrator’s reaction vessel and dissolve the KHP with water, we complete the titration and find that it takes 18.64 mL of NaOH to reach the end point. To find the uncertainty in this volume we need to consider, as shown in Figure 16.2.1 , three sources of uncertainty: the automated titrator’s calibration, the ambient temperature, and any bias in determining the end point.
To find the uncertainty from the automated titrator’s calibration we examine the instrument’s certificate, which indicates a range of \(\pm 0.03 \text{ mL}\) for a 20-mL piston. Because we expect that an effective manufacturing process is more likely to produce a piston that operates near the center of this range than at the extremes, we will assume a triangular distribution. Our estimate of the uncertainty due to the calibration, u(Vcal) is
\[u(V_\text{cal}) = \frac {0.03 \text{ mL}} {\sqrt{6}} = \pm 0.012 \text{ mL} \nonumber\]
To determine the uncertainty due to the lack of temperature control, we draw on our prior work in the lab, which has established a temperature variation of \(\pm 3 \text{°C}\) with a confidence level of 95%. To find the uncertainty, we convert the temperature range to a range of volumes using water’s coefficient of expansion
\[(2.1 \times 10^{-4} \text{°C}) \times (\pm 3 \text{°C}) \times 18.64 \text{ mL} = \pm 0.012 \text{ mL} \nonumber\]
and then estimate the uncertainty due to temperature, u(Vtemp) as
\[u(V_\text{temp}) = \frac {\pm 0.012 \text{ mL}} {1.96} = \pm 0.006 \text{ mL} \nonumber\]
Titrations using NaOH are subject to a bias due to the adsorption of CO2, which can react with OH–, as shown here.
\[\ce{CO2}(aq) + \ce{2OH-}(aq) \ce{->} \ce{CO3^{2-}}(aq) + \ce{H2O}(l) \nonumber\]
If CO2 is present, the volume of NaOH at the end point includes both the NaOH that reacts with the KHP and the NaOH that reacts with CO2. Rather than trying to estimate this bias, it is easier to bathe the reaction vessel in a stream of argon, which excludes CO2 from the automated titrator’s reaction vessel.
Adding together the uncertainties for the piston’s calibration and the lab’s temperature gives the uncertainty in the uncertainty in the volume of NaOH, u(VNaOH) as
\[u(V_\ce{NaOH}) = \sqrt{(0.012 \text{ mL})^2 + (0.006 \text{ mL})^2} = \pm 0.013 \text{ mL} \nonumber\]
Uncertainty in the Purity of KHP
According to the manufacturer, the purity of KHP is \(100 \% \pm 0.05 \%\), or \(1.0 \pm 0.0005\). Assuming a rectangular distribution, we report the uncertainty, u(PKHP) as
\[u(P_\ce{KHP}) = \frac {\pm 0.0005} {\sqrt{3}} = \pm 0.00029 \nonumber\]
Uncertainty in the Molar Mass of KHP
The molar mass of C8H5O4K is 204.2212 g/mol, based on the following atomic weights: 12.0107 for carbon, 1.00794 for hydrogen, 15.9994 for oxygen, and 39.0983 for potassium. Each of these atomic weights has an quoted uncertainty that we can convert to a standard uncertainty assuming a rectangular distribution, as shown here (the details of the calculations are left to you).
| element |
quoted uncertainty (per atom) |
standard uncertainty (per atom) |
number of atoms | total uncertainty |
|---|---|---|---|---|
| carbon | \(\pm 0.008\) | \(\pm 0.00046\) | 8 | \(\pm 0.00368\) |
| hydrogen | \(\pm 0.00007\) | \(\ 0.000040\) | 5 | \(\pm 0.00020\) |
| oxygen | \(\pm 0.0003\) | \(\pm 0.00017\) | 4 | \(\pm 0.00068\) |
| potassium | \(\pm 0.0001\) | \(\pm 0.000058\) | 1 | \(\pm 0.000058\) |
Adding together these uncertainties gives the uncertainty in the molar mass, u(MKHP), as
\[u(FW_\ce{KHP}) = \sqrt{(0.00368)^2 + (0.00020)^2 + (0.00068)^2 + (0.0.000058)^2} = \pm 0.0037 \text{ g/mL} \nonumber\]
Uncertainty in the Titration's Repeatability
To estimate the uncertainty due to repeatability we complete five titrations, obtaining the following results for the concentration of NaOH: 0.1021 M, 0.1022 M, 0.1022 M, 0.1021 M, and 0.1021 M. The relative standard deviation, srel, for these titrations is
\[s_{rel} = \frac {s} {\overline{X}} = \frac {5.48 \times 10^{-5}} {0.1021} = \pm 0.0005 \nonumber\]
If we treat the ideal repeatability as 1.0, then the uncertainty due to repeatability, u(R), is the relative standard deviation, or, in this case, 0.0005.
Combining the Uncertainties
The table below summarizes the five primary sources of uncertainty.
| term | source | value, x | uncertainty, u(x) |
|---|---|---|---|
| \(m_\ce{KHP}\) | mass of KHP | 0.3888 g | \(\pm 0.00012\) g |
| \(V_\ce{naOH}\) | volume of NaOH at endpoint | 18.64 mL | \(\pm 0.013\) mL |
| \(P_\ce{KHP}\) | purity of KHP | 1.0 | \(\pm 0.00029\) |
| \(M_\ce{KHP}\) | molar mass of KHP | 204.2212 g/mol | \(\pm 0.0037\) g/mol |
| \(R\) | repeatability | 1.0 | \(\pm 0.0005\) |
As described earlier, we calculate the concentration of NaOH we use the following equation, which is slightly modified to include a term for the titration’s repeatability, which, as described above, has a value of 1.0.
\[C_\ce{NaOH} = \frac {1000 \times m_\ce{KHP} \times P_\ce{KHP}} {FW_\ce{KHP} \times V_\ce{NaOH}} \times R \nonumber\]
Using the values from our table, we find that the concentration of NaOH is
\[C_\ce{NaOH} = \frac {1000 \times 0.3888 \times 1.0} {204.2212 \times 18.64} \times 1.0 = 0.1021 \text{ M} \nonumber\]
Because the calculation of CNaOH includes only multiplication and division, the uncertainty in the concentration, u(CNaOH) is given by the following propagation of uncertainty.
\[\frac {u(C_\ce{NaOH})} {C_\ce{NaOH}} = \frac {u(C_\ce{NaOH})} {0.1021} = \sqrt{\frac {(0.00012)^2} {(0.3888)^2} + \frac {(0.00029)^2} {(1.0)^2} + \frac {(0.0037)^2} {(204.2212)^2} + \frac {(0.013)^2} {(18.64)^2} + \frac {(0.0005)^2} {(1.0)^2}} \nonumber\]
Solving for u(CNaOH) gives its value as \(\pm 0.00010 \text{ M}\), which is the final uncertainty for the analysis.
Evaluating the Sources of Uncertainty
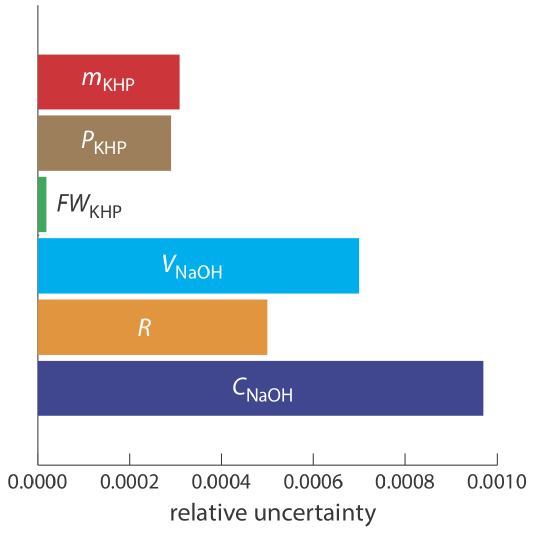
Figure 16.2.3 shows the relative uncertainty in the concentration of NaOH and the relative uncertainties for each of the five contributions to the total uncertainty. Of the contributions, the most important is the volume of NaOH, and it is here to which we should focus our attention if we wish to improve the overall uncertainty for the standardization.