Skip to main content
Chemistry LibreTexts

Crystal Field Theory (Worksheet)

  1. Last updated
  2. Save as PDF
  • Page ID
    127053

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Name: ______________________________

    Section: _____________________________

    Student ID#:__________________________

    Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.

    Model I. The d-Orbitals

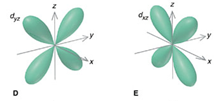
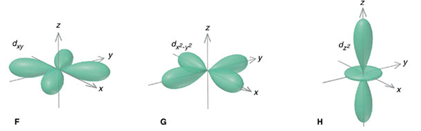
    clip_image007.pngclip_image008.png

    Key Questions

    1. Name the d-orbitals that are on-axis orbitals.
    2. Draw just the on-axis orbitals on the same coordinate set. What shape do they most closely represent?
    3. What does it mean to be on-axis and off-axis?

    Model II. Splitting in the Octahedral Field Case

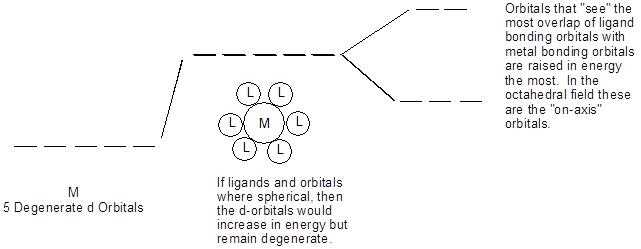
    clip_image009.png

    Key Questions

    1. What does degenerate mean?
    2. What are the names of the three d-orbitals that are lowered in energy?
    3. Explain what is meant by “the most overlap ligand bonding orbitals with metal bonding orbitals”?
    4. If the orbital overlap between atoms A and B is stronger than that between C and D, which pair has the shortest bond? Explain.
    5. Draw the molecule PtCl42-, it adopts a square planar geometry.
    6. Using the model for the octahedral field, generate a d-orbital splitting diagram for a square planar geometry.
    7. Knowing that the ligands in a tetrahedral field approach “off-axis”, draw the molecule NiCl42- which is tetrahedral then generate a d-orbital splitting diagram for a tetrahedral geometry.

    Model III. High Field, Low Spin; Low Field, High Spin

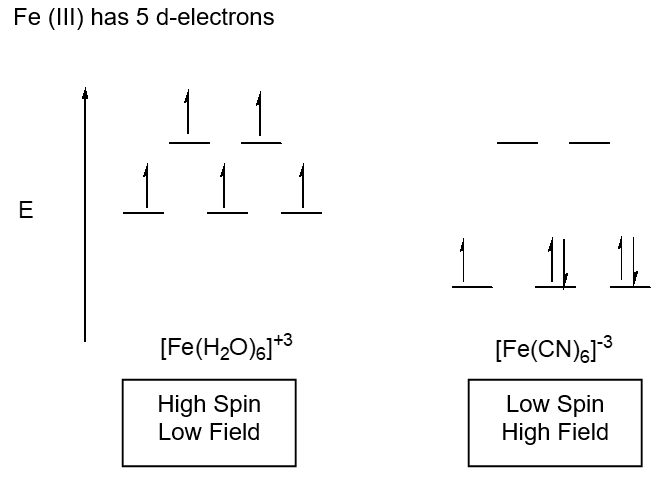
    ed6a9069e966c206e9d4c77b03378c70c.png

    Gouey Balance – measures changes in magnetic moment such as the number of unpaired electrons

    Key Questions

    1. Is the energy difference between the t2g level and the eg level higher or lower in [Fe(H2O)6]+3 or [Fe(CN)6]-3? Explain.
    2. What is the consequence of the difference in energy?
    3. Why is one splitting diagram labeled high spin/low field and the other low spin/high field? (field refers to energy and spin to the number of unpaired electrons)
    4. If the Gouey Balance senses magnetic moment differences, can it be used to determine if a compound is high spin/low field? Explain.
    5. Draw the two splitting diagrams that could arise for d6 metal center in an octahedral field. Be sure to label them carefully. Will the Gouey Balance be useful here to determine if the complex is high or low field? Explain.

    Model IV. Spectrochemical Series and \(\pi^{*}\)-backbonding

    I- < Br- < [NCS]- < Cl- < F- < [OH]- < [ox]-2 H2O < [NCS]- < NH3 < en < bpy < phen < [CN]- \(\approx\) CO
    Lowest Crystal Field Splitters Highest Crystal Field Splitters

    Ligands at the right of the spectrochemical series are high field splitters because they have empty \(\pi^{*}\) orbitals that the M center can dump electrons into to make a stronger/shorter bond.

    clip_image0010.png

    Key Questions

    1. What do ligands at the left of the spectrochemical series have in common? Draw the electron box diagrams for Br-, how does Br- bond to a metal center?
    2. Draw the molecular orbital diagram for CN-. What similarities to CO do you notice? Does it make sense that CN- and CO should be in roughly the same place on the spectrochemical series?
    3. What do the abbreviations en, bpy and phen stand for? Draw the structures of these three ligands.
    4. Draw the molecular orbital diagrams for H2O and NH3, why is NH3 a stronger crystal field splitter than H2O? Remember to hybridize the atomic orbitals on the central atom first.
    5. If a metal and a ligand can have p* backbonding, what do you expect the bond length between the ligand and metal to be, more like a double bond or more like a single bond?
    6. Sum up crystal field theory in your own words beginning with d-orbitals, splitting diagrams, the influence of field on magnetics and finally why some compounds exhibit high crystal field splitting while others low crystal field splitting.

    Exercise \(\PageIndex{1}\)

    1. Create a ligand field splitting diagram for a trigonal bipyramid geometry. Explain why the d-orbitals are higher or lower in energy with respect to geometry.
    2. Compare the molecules Pt(CN)42- with PtCl42- both of which adopt a square planar geometry. Which of these molecules would be high spin/low field? Explain.
    3. Explain why [NCS]- is a low field splitter while [NCS]-is a high field splitter.
    4. A complex triggers the Gouey balance indicating that it is paramagnetic. Is the complex, Co(NH3)6+3 or CoCl6-3? Explain.

    Reference

    • Kelley J. Donaghy, SUNY-ESF

    Crystal Field Theory (Worksheet) is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by LibreTexts.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      License
      CC BY-NC-SA
      License Version
      4.0
      Show Page TOC
      no on page
    2. Tags
      This page has no tags.