Coordination Compounds (Worksheet)

Name: ______________________________

Section: _____________________________

Student ID#:__________________________

Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.

Learning Objectives

• Identify the coordination number and inner and outer coordination spheres
• Demonstrate knowledge of coordination geometries
• Recognize common ligands and molecules and ions that are suitable as ligands

Transition metals form a large number of compounds with exciting properties. In addition, transition metal complexes with organic ligands (organometallic compounds) and transition metal complexes in biological systems often possess the same geometries.

Coordination Compounds

Model 1: An inner-sphere complex consists of the metal ion or atom and the ligands directly attached to the metal. The coordination number is the number of ligands directly attached to the metal. Because the inner-sphere complex is frequently charged, this complex is often electrostatically attracted to ligands or solvent molecules without displacement of the directly attached ligands. This is called an outer-sphere complex.

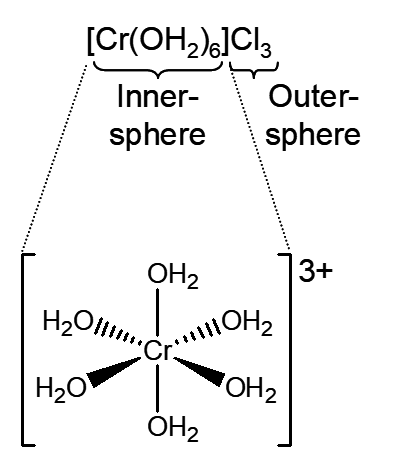
Critical Thinking Questions

1. What is the coordination number of the following metal ion compounds?
   1. [Fe(NH₃)₆]Cl₃
   2. K₂[PtCl₄]
   3. K₃[Co(CN)₅(H₂O)]
   4. [Co(NH₃)₄Cl₂]Cl • H₂O
   5. [Ni(CN)₅]^3-
2. Identify the metal ion and ligands (with charges) for these coordination complexes:

	Metal ion	Ligands
a. K2[PtCl4]
b. [Pt(NH3)2Cl2]
c. [Co(NH3)6]Cl3
d. [Ni(CO)4]

3. Identify the inner-sphere and outer-sphere ligands for each compound in CTQ 1 and 2.
4. In his studies, Werner noted that the reactivities of these compounds with silver were significantly different: $$\begin{split} CoCl_{3} \cdot 6\; NH_{3} + excess\; Ag^{+} & \rightarrow 3\; AgCl(s) \\ CoCl_{3} \cdot 5\; NH_{3} + excess\; Ag^{+} & \rightarrow 2\; AgCl(s) \\ CoCl_{3} \cdot 4\; NH_{3} + excess\; Ag^{+} & \rightarrow 3\; AgCl(s) \end{split}$$Identify the inner-sphere and outer-sphere for the complexes described above. Write the chemical formulas for each (in the form [MX_m]Y_n).

Coordination Geometries

Information: Coordination compounds exhibit a variety of geometries. Common geometries include examples of various coordination compounds including 4 coordinate, 5 coordinate, and 6 coordinate. By far, octahedral geometry is the most common for coordination compounds.

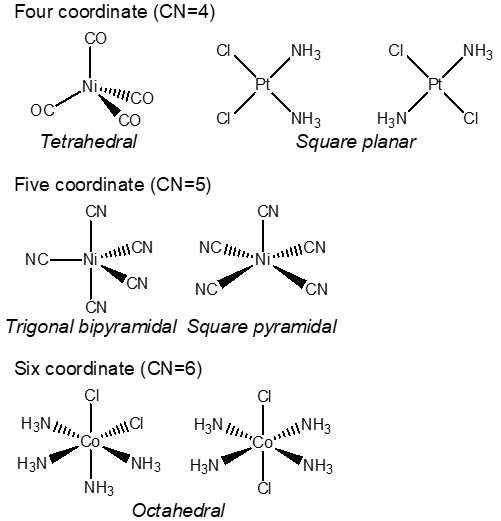
Coordination number 4: d⁸ metals typically form square planar complexes; for example, Ni(II), Pd(II), and Pt(II). Many other metals form tetrahedral complexes.

Coordination number 5: Trigonal bipyramidal and square pyramidal geometries are very close in energy. Many 5 coordinate complexes have geometries between the two.

Coordination number 6: The most common coordination number is six and the most common geometry is octahedral.

Critical Thinking Questions

5. Sketch the possible geometries for the inner sphere complex for each compound in CTQ 1, 2, and 4.

Problems

1. Four complexes of cobalt(III) with ammonia had been discovered when Alfred Werner began study of these transition metal complexes:

Complex	Color	Early Name
CoCl3 • 6NH3	Yellow	Luteo complex
CoCl3 • 5NH3	Purple	Purpureo complex
CoCl3 • 4NH3	Green	Praseo complex
CoCl3 • 4NH3	Violet	Violeo complex

Interestingly, two of the compounds described in the table have the same empirical formulas but one is green and the other violet. Suggest a reason for the different colors of the two CoCl₃ • 4NH₃ complexes described above.

2. The conductivities of equimolar solutions of [Pt(NH₃)₄]Cl₂, [Pt(NH₃)₃Cl]Cl, [Pt(NH₃)₂Cl₂], K[PtNH₃Cl₃], and K₂[PtCl₄] were measured. The results are plotted in Figure 1. Identify which point represents each compound. Briefly explain how you were able to identify the compounds.

References

• Jens-Uwe Kuhn, Santa Barbara City College
• Jessica Martin, Northeastern State University