Geometry and Isomerism in Coordination Compounds (Worksheet)

Last updated
Save as PDF

Page ID: 127050

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Name: ______________________________

Section: _____________________________

Student ID#:__________________________

Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.

Learning Objectives

Identify various types of isomers
Predict the types of isomers possible from molecular formulas of coordination compounds
Identify the geometry of a compound from the numbers and types of isomers

Coordination compounds can form different isomers. Two main types of isomerism exhibited by coordination compounds are stereoisomerism and structural isomerism. Stereoisomers include both geometric and optical isomers. Structural isomers include linkage, ionization, coordination, and hydrate isomers. The reactivities and properties of different isomers are often not the same and contribute to the wonderful array of applications of coordination compounds.

Stereoisomerism

Model 1: A square planar complex with the formula [MA₂B₂] can form two distinct isomers, a cis and a trans (where M represents a metal ion or atom and A and B are ligands).

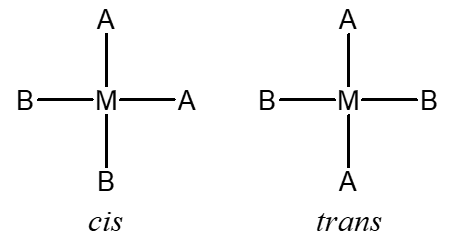
Critical Thinking Questions

Similar to the case described in Model 1, a square-planar complex with the formula [MA₂BC] can form a cis and a trans isomer. Draw and label the two possible isomers.
A square-planar complex with formula [MABCD] can form three isomers. These isomers are called “A trans to B” and so on. Draw and label the three possible isomers.
A tetrahedral complex with the formula [MABCD] can form two enantiomers. Draw the two possible structures. (Hint: think back to organic chemistry!)
Cis and trans isomers are possible for octahedral complexes with the formula [MA₄B₂]. Draw and label the two possible isomers.
Two isomers are possible for octahedral complexes with the formula [MA₃B₃]. In one isomer, the three A ligands are arranged on one plane with the three B ligands in a perpendicular plane; this configuration is called the meridional or mer isomer. In the other isomer, the three A ligands are adjacent and occupy the corners of one triangular face (as do the B ligands); this configuration is called the facial or fac isomer. Draw and label the two possible isomers for an octahedral complex with the formula [MA₃B₃].
Five isomers are possible for an octahedral complex with the formula [MA₂B₂C₂]. Draw and label the possible isomers (don’t forget to consider enantiomeric pairs!).
Use your answers from CTQ 1-6 to complete the summary table below.

Geometry	Names	Number of isomers	Number of enantiomeric pairs
Coordination Number=4
Square-planar
[MA₂B₂]	cis trans	2	n/a
[MA₂BC]	cis trans	2	n/a
[MABCD]
Tetrahedral
[MABCD]
Coordination Number=6
Octahedral
[MA₃B₃]
[MA₂B₂C₂]

Other types of isomers

Model 2: Linkage isomers are possible for ambidentate ligands such as the thiocyanate ion (NCS^-) which can attach via the nitrogen or the sulfur atom or NO₂^- which can attach via the nitrogen or the oxygen atom.

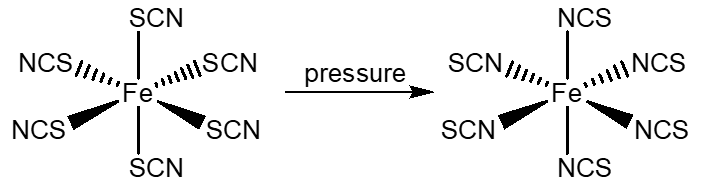
Hexathiocyanato ferrate undergoes isomerization to hexaisothiocyanato ferrate under high pressures. The conversion is essentially complete at 150 kb (Fung and Drickamer, PNAS 1958, 62, 38-43).

Ionization isomers are formed when the ligand and counter ion are exchanged: for example, a compound consisting of Pt(NH₃)₄ with two Cl^- and two Br^- could form [Pt(NH₃)₄Cl₂]Br₂ or [Pt(NH₃)₄Br₂]Cl₂.

Coordination isomers form when different complex ions can form from the same molecular formula: CoCr(NH₃)₆(CN)₆ could produce [Co(NH₃)₆][Cr(CN)₆] and [Cr(NH₃)₆][Co(CN)₆].

Hydrate isomers are formed when at least one of the ligands in a coordination complex is water. [Co(NH₃)₄(OH₂)Cl]Cl₂ and [Co(NH₃)₄Cl₂]Cl·H₂O are examples of hydrate isomers.

Critical Thinking Questions

Identify the type of isomerism possible for the following complexes
1. [RuBr(NH₃)₅]Cl and [RuCl(NH₃)₅]Br
2. [Co(NO₂)(NH₃)₅]²⁺
3. [Cr(OH₂)₆]Cl₃ and [Cr(OH₂)₅Cl]Cl₂
CrCl₃• 6 H₂O has three distinctly different crystalline compounds, A is violet, B is blue-green, and C is dark green. Each compound is octahedral. Upon titration with excess silver nitrate, A produces three equivalents of AgCl, B produces two equivalents of AgCl, and C produces one equivalent of AgCl. Determine the formulas of the compounds. Match the colors to the formulas. What type of isomers are these compounds?

Problems

Are isomers possible for the following coordination compounds? If so, draw the isomers and label each:
1. [IrCl(CO)(PPh₃)₂]
2. [Co(NO₂)₃(NH₃)₃] (NO₂^- linked through the N)
3. [CoCl₂(NH₃)₃(OH₂)]⁺
4. [CoBrClI(OH₂)] (tetrahedral)
5. [Fe(CN)₂(CH₃NC)₄]
How many isomers are possible for the complex [Cr(OH₂)₃BrClI]? Draw each.

References

Jens-Uwe Kuhn, Santa Barbara City College
Jessica Martin, Northeastern State University