7.5: Dipole-dipole attractions
- Page ID
- 138868
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When two different kinds of atoms are connected to each other, the electrons between them are typically not shared evenly. That's because in most cases, two different atoms would have two different electronegativity values. One atom would be more electronegative than the other. It would have a stronger attraction for the electrons in the shared bond, and the electrons would be a little bit more attracted to that atom than the other.
Remember, electronegativity is a periodic trend. As we move to the right in the periodic table, more and more protons are added to the nucleus, and so atoms on the right attract electrons more strongly that do the atoms on the left. Also, as we move from top to bottom of the periodic table, the valence shells of the atoms become larger; that means valence electrons are getting farther from the nucleus, so they are less tightly held. Those two factors, distance and amount of charge, control the strength of interaction between charged particles.

The periodic table above shows Pauling electronegativity values. There are different ways to calculate electronegativity, but the Pauling scale is very commonly used. Calculating the Pauling scale depends on being able to observe compounds, so the noble gases are not usually given a value in this scale, because they normally don't form any compounds.
For example, when a carbon atom is bonded to a fluorine atom, there is an electronegativity difference between the two atoms. There is a difference in electronegativity values of almost 1.5 units between these two atoms. Fluorine is more electronegative than carbon because it has more protons in the nucleus than carbon. The electrons are pulled closer to the fluorine than to the carbon. A carbon-fluorine bond is polarized towards the fluorine. A molecule like fluoromethane, CH3F, has a permanent dipole.
Note that there are also dipoles in C-H bonds, but they are so much smaller than the ones in the C-F bond that they do not matter. The overall dipole has a buildup of negative charge on the fluorine.
You can imagine that molecules with permanent dipoles would interact with each other much more strongly than molecules that rely on temporary dipoles in order to stick together. Molecules with no natural dipole will stick only loosely together, but molecules with permanent dipoles will stick to each other easily.
Ethane, C2H6 (sometimes written CH3CH3, suggesting two carbons are each connected to three hydrogens, and also to each other), and formaldehyde, CH2O, have different formulae but the same molecular weight. Based on weight alone, it would take about the same amount of energy to move an ethane molecule and a molecule of formaldehyde.

The two molecules also have somewhat similar shapes, unlike neopentane and pentane. At room temperature, ethane and formaldehyde are both gases. Nevertheless the two compounds have very different boiling points; formaldehyde becomes liquid around -20 oC, which would be a very cold winter day in, say, Chicago. Ethane does not become liquid unless it is cooled to around -90 oC, a cold winter day on Neptune, at which point formaldehyde is just about ready to freeze solid.
The difference between these two molecules must be due to the oxygen atom in formaldehyde. Oxygen, the second most electronegative element in the periodic table, can form some very polar bonds. The difference between carbon and oxygen is 0.89 units, almost a full electronegativity unit. The permanent dipole that results between the oxygen and carbon makes the formaldehyde molecules much stickier than the ethane molecules, which depend on fleeting London interactions if they are going to hold on to each other.
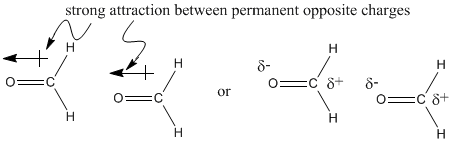
In contrast, the difference in electronegativity between carbon and hydrogen is actually pretty small (about 0.35 units, based on the Pauling scale). The tiny dipole in the C-H bond is so much smaller than the one in the C=O bond that it really isn't a factor here.
Taking that story a little further, hydrocarbons (molecules made up of hydrogen and carbon) are the most common example of non-polar compounds, because their bonds are either completely nonpolar C-C bonds or else C-H bonds with very low polarity. There is a tiny dipole in a C-H bond, but it isn't enough to make the molecules attract each other very well. Furthermore, there tend to be a lot of C-H bonds in a hydrocarbon pointing in all sorts of directions; an approaching molecule would be unlikely to encounter either a fully positive end or a fully negative end of the molecule. In the end, all those little dipoles in all those C-H bonds end up cancelling each other out.
There are other variations on dipole interactions that are pretty common. For example, you could imagine that a dipolar molecule would interact pretty strongly with an ion. We will take a look at that situation shortly when we think about how mixtures of different compounds interact with each other. However, perhaps the most important variation in organic chemistry is hydrogen bonding.
Problem SP5.1.
Comment on dipole moments in the following compounds and predict their relative boiling points.
a) 1-chlorobutane vs. pentane b) triethylamine vs. 3-ethylpentane c) diethyl ether vs. pentane
Sometimes a molecule that contains polar bonds is not really polar overall. Carbon dioxide is a good example. Polar molecules strongly attract each other because the more negative end of one molecule is attracted to the more positive end of the next molecule via electrostatics. Opposites attract. In carbon dioxide, however, both ends of the molecule are more negative. How can they attract each other?
There's more to it. Dipoles are "vector quantities". That means it isn't just the amount of charge separation that matters; it's also the direction of separation. In carbon dioxide, a linear molecule, there are two polar bonds. Those polar bonds point directly away from each other. The dipole of one bond balances out the dipole of the other bond. Overall, the molecule does not have a dipole.
Water, on the other hand, is a different case. Like carbon dioxide, water has two polar bonds. However, the bonds in water do not lie in a straight line like the ones in carbon dioxide. They are at an angle to each other instead. That means their dipoles are not quite pointing in opposite directions. As a result, water has an overall dipole moment.
At the extreme, a polar bond can get to the point that one atom is pulling the electrons so strongly toward itself that it pulls them completely away from the other atom. The first atom becomes an anion, and the second atom becomes a cation. At this point, we have an ionic bond, rather than a covalent one. How different must the electronegativity values be in order to have an ionic bond? The usual rule of thumb is a difference of about 1.6 electronegativity units. So, for example, all of the blue atoms in the periodic table above would form ionic bonds with all of the red atoms. The green atoms would form ionic bonds with most of the dark red atoms, but not with the light red ones.
Problem SP5.2.
The dipole moment of a molecule (essentially the size of its dipole) can be calculated from the dielectric constant of a material, which can be measured experimentally on a bulk quantity of the compound. The dipole moment of chloromethane, 12.9 D, is higher than that of dichloromethane, 9.08 D, even though dichloromethane has a greater number of polar bonds than chloromethane. Explain why.
Problem SP5.3.
Dichloromethane nonetheless has a higher boiling point (39 °C) than chloromethane ( -24 °C). Explain why.
Problem SP5.4.
Comment on dipole moments in the following compounds and predict their relative boiling points.
a) butane and ethyl methyl ether
b) ethyl methyl ether and 2-propanone
c) trimethylamine and propanenitrile
d) 2-propanone and 2-chloropropane
Problem SP5.5.
a) Draw the Lewis structure for each molecule with the correct electronic geometry.
b) Draw in dipole moments.
c) Decide if the molecule is polar.



