Chemical Equations of Food Additives

We've examined the properties of cuprous iodide while discussing its use as a salt additive. From these properties it can be identified as CuI. The equation for the formation of cuprous iodide would look like this:

\[\ce{Cu} + \ce{I}_2 \rightarrow \ce{CuI}\label{1}\]

But we must be sure that the law of conservation of mass is obeyed. The same number of atoms (or moles of atoms) of a given type must appear on each side of the equation. This reflects our belief in Dalton’s third postulate that atoms are neither created, destroyed, nor changed from one kind to another during a chemical process. When the law of conservation of mass is obeyed, the equation is said to be balanced.

Balancing Equations

Equation \(\ref{1}\) is not balanced because there are 2 iodine atoms (in I₂) on the left side of the equation and only 1 on the right.

An incorrect way of obtaining a balanced equation is to change this to

\[\ce{Cu} + \ce{I}_2 \rightarrow \cancel{\ce{CuI}_2}\label{2}\]

This equation is wrong because we had already determined from the properties of the product that the product was CuI. Equation \(\ref{2}\) is balanced, but it refers to a different reaction which produces a different product. The equation might also be incorrectly written as

\[\ce{Cu} + \cancel{\ce{I}} \rightarrow \ce{CuI}\]

The symbol I suggests that iodine atoms were involved, but we know that iodine exists as diatomic molecules.

In balancing an equation you must remember that the subscripts in the formulas have been determined experimentally. Changing them indicates a change in the nature of the reactants or products. It is permissible, however, to change the amounts of reactants or products involved. For example, the equation in question is correctly balanced as follows:

\[\ce{2 Cu} + \ce{I}_2 \rightarrow \ce{2 CuI}\]

The 2 written before the symbol Cu is called a coefficient. It indicates that on the microscopic level 2 Cu atoms are required to react with one iodine molecule. On a macroscopic scale the coefficient 2 means that 2 mol Cu atoms are required to react with 1 mol I₂ molecules.

To summarize: Once the formulas (subscripts) have been determined, an equation is balanced by adjusting coefficients. Nothing else may be changed.

 

We have seen that copper may form an unstable cupric iodide (CuI₂), but this decomposes immediately to cuprous iodide and iodine. Balance the equation for this process:

\[\ce{CuI2 -> CuI + I2} \nonumber \]

Solution

Although Cu is balanced, there are 3 I atoms on the right and only 2 on the left. A coefficient of 2 with CuI₂ will help:

\[\ce{ 2 CuI2 -> CuI + I2} \nonumber\]

Now I is still not balanced. We need 2 CuI molecules on the right:

\[\ce {2 CuI2 -> 2CuI + I2} \nonumber\]

We now have 2 Cu atoms and 4 I atoms on each side, and so balancing is complete.

Most chemists use several techniques for balancing equations.^[1] For example, it helps to know which element you should balance first. When each chemical symbol appears in a single formula on each side of the equation (Example \(\PageIndex{1}\)), you can start wherever you want and the process will work. When a symbol appears in three or more formulas, however, that particular element will be more difficult to balance and should usually be left until last.

Metabolism of Sorbitol and Xylol

The sugar substitutes sorbitol and xylitol appear frequently on labels of packaged snack foods. They are sugar alcohols that occur naturally in fruits, but are probably made synthetically for many products. They are roughly as sweet as sucrose, and made by hydrogenating one C=O group on a sugar to a C-OH group, as shown below. They are nutritive sweeteners because they do have calories--about 2.6 Cal per gram compared to 4 Cal per gram for most sugars, so they are often found in "diet" foods like soft drinks, sugar-free gum, and ice cream.^[2] These are both laxatives to some degree, and sometimes lead to bloating, flatulence, and diarrhea.^[3]

Figure \(\PageIndex{2}\) Glucose

Example \(\PageIndex{2}\): Writing a Balanced Equation

When sorbitol (C₆H₁₄O₆) is metabolized, or burned in oxygen gas (O₂), the only products are carbon dioxide(CO₂) and water. Write a balanced equation to describe this reaction.

Solution

First write an unbalanced equation showing the correct formulas of all the reactants and products:

\[\ce{C6H14O6 + O2 -> CO2 + H2O}\nonumber\]

We note that O atoms appear in all formulas, two on the left and two on the right. Therefore we balance C and H first. The formula C₆H₁₄O₆ determines how many C and H atoms must remain after the reaction, and so we write coefficients of 6 for CO₂ and 7 for H₂O:

\[\ce{C6H14O6 + O2 -> 6 CO2 + 7 H2O}\nonumber\]

We now have a total of 19 O atoms on the right-hand side, and 6 in the sorbitol, so we're lacking 13 on the left. At first, the fact that O atoms come in pairs as O₂ seems to present a problem but we can balance the equation by using a coefficient of \(\dfrac{13}{2}\) in front of O₂:

\[\ce{C6H14O6 + 13/2 O2 -> 6 CO2 + 7 H2O}\nonumber\]

Usually it is preferable to remove fractional coefficients since they might be interpreted to mean a fraction of a molecule. (One-half of an O₂ molecule would be an O atom, which has quite different chemical reactivity.) Therefore we multiply all coefficients on both sides of the equation by two to obtain the final result:

\[\ce{2 C6H14O6 + 13 O2 -> 12 CO2 + 14 H2O}\nonumber\]

(Sometimes, when we are interested in moles rather than individual molecules, it may be useful to omit this last step. Obviously the idea of half a mole of O₂ molecules, that is, 3.011 × 10²³ molecules, is much more tenable than the idea of half a molecule.)

Another useful technique is illustrated in Example \(\PageIndex{2}\). When an element (such as O₂) appears by itself, it is usually best to choose its coefficient last. Furthermore, groups such as NO₃, SO₄, etc., often remain unchanged in a reaction and can be treated as if they consisted of a single atom. When such a group of atoms is enclosed in parentheses followed by a subscript, the subscript applies to all of them. That is, the formula involves Ca(NO₃)₂ involves 1 Ca, 2N and 2 × 3 = 6 O atoms.

Potassium Bromate in Flour

Potassium Bromate (KBrO₃) is added to flour as a conditioner which enhances the structure of bread.^[4] It may do this by forming disulfide bonds in a reaction like the one in Example 3, between two cysteine amino acids. The actual mechanism for bromate action is still not known, but it may involve oxidation of glutathione to give a disulfide link (analagous to cysteine)^[5] This mechanism has been demonstrated in pound cake, where the links are in egg proteins^[6][7] The function of the KBrO₃ is to remove the 2 electrons, which is necessary to form the disulfide bond, as shown in the figure below. Each of the cysteine amino acids would be in a protein chain, so the reaction would link two chains, imparting cohesion to the dough.

Figure \(\PageIndex{3}\) Cysteine,C₃H₆(NO₂)SH. The S atom is in yellow

Figure \(\PageIndex{4}\) Formation of a disulfide bond. "R" represents the C₃H₆(NO₂) part of cysteine

Figure \(\PageIndex{5}\) The S-S linkage between cysteine molecules

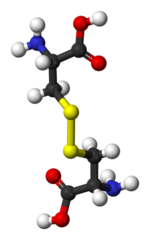
But potassium bromate is a proven carcinogen,^{[8] [9]} and it is only allowed in foods in the US because it is assumed that bakers will add the right amount and provide the correct conditions of temperature and baking time so that the equation below goes to completion, producing only Br^-, which is harmful only at levels high enough so that it competes with iodine uptake. Bromate is banned in most of Europe; UK banned bromate in bread in 1990, Canada in 1994. Many US bakers still use it; look at the label!

Example \(\PageIndex{3}\): Balance the Reaction

Balance the for the reaction of potassium bromate with 2 cysteine molecules (C₃H₆NO₂)SH, where the part of the molecule in parentheses is unchanged, so it can be balanced as a single unit.

\(\ce{KBrO3 + (C3H6NO2)SH -> KBr + H2O + (C3H6NO2)2S2}\)

Solution

The K and Br are balanced. We note that 3 oxygen atoms are found in KBrO₃ on the left, but only 1 in H₂O on the right. So one starting place would be to balance the oxygen:

\(\ce{KBrO3 + (C3H6NO2)SH -> KBr + 3 H2O + (C3H6NO2)2S2}\)

Now there are 6 H in the 3 H₂O on the right, but only 1 in the (C₃H₆NO₂)SH molecules on the left, so we can add a coefficient of 6:

\(\ce{KBrO3 + 6 (C3H6NO2)SH -> KBr + 3 H2O + (C3H6NO2)2S2}\)

But now we have 6 (C₃H₆NO₂)SH, so we'll need 3 of the sulfur bridged species on the right:

\(\ce{KBrO3 + 6 (C3H6NO2)SH -> KBr + 3 H2O + 3 (C3H6NO2)2S2}\)

Notice that, in this example, the rule of balancing first those elements whose symbols appeared in the smallest number of formulas doesn't help, because H and O both appear in two of them. But if we started by balancing H, (say by adding 2 before (C₃H₆NO₂)SH, that step would have to be redone as soon as we went back to balance O. More algorithms for balancing equations will be developed later, in reactions in aqueous solutions.

The balancing of chemical equations has an important environmental message for us. If atoms are conserved in a chemical reaction, then we cannot get rid of them. In other words we cannot throw anything away. There are only two things we can do with atoms: Move them from place to place or from compound to compound. Thus when we "dispose" of something by burning it, dumping it, or washing it down the sink, we have not really gotten rid of it at all. The atoms which constituted it are still around someplace, and it is just as well to know where they are and what kind of molecule they are in. Discarded atoms in places where we do not want them and in undesirable molecules are known as pollution.

From ChemPRIME: 2.12: Balancing Chemical Equations

References

1. ↑ Laurence E. Strong, Balancing Chemical Equations, Chemistry, vol. 47, no. 1, pp. 13-16, January 1974, discusses some techniques in more detail.
2. ↑ http://en.Wikipedia.org/wiki/Sorbitol
3. ↑ http://en.Wikipedia.org/wiki/Xylitol
4. ↑ http://www.inchem.org/documents/jecfa/jecmono/v18je13.htm
5. ↑ H.-D. Belitz, W. Grosch, P. Schieberle, Food Chemistry,Springer; 4th ed. 2009, p. 719
6. ↑ http://pubs.acs.org/doi/full/10.1021/jf100340j
7. ↑ http://pubs.acs.org/doi/abs/10.1021/jf100340j
8. ↑ http://www.cspinet.org/new/bromate.html
9. ↑ http://www.ncbi.nlm.nih.gov/pmc/articles/PMC1567851/

Contributors and Attributions

• Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.