Electromagnetic Radiation in Technologies

Ever wonder exactly how automatic doors or shoplift-preventing sensors work? Maybe not, but surely something as important as music and video files, when related to the electromagnetic spectrum, would pique interest. So much of the modern world relies on the wave theory of the electron and the many types of electromagnetic radiation.

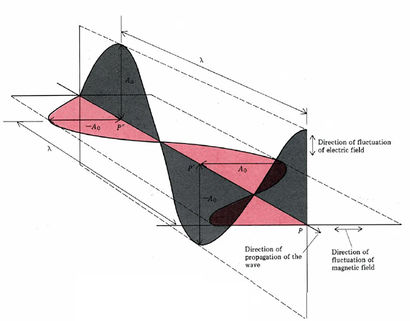
Figure \(\PageIndex{1}\) Fluctuating electric and magnetic fields associated with electromagnetic waves. A₀ is the maximum amplitude of the wave; λ is the wavelength.

The wave theory can be thought of as periodically varying electric and magnetic fields (electromagnetic waves), which follow paths similar to sine curves. The above image indicates the relationship of these fluctuating electric and magnetic fields. It also illustrates the maximum amplitude A₀ and the wavelength λ associated with the wave. The intensity of a wave is associated with the square of its amplitude.

The wavelength λ is inversely related to the frequency v, defined as the number of crests (points of maximum amplitude, nodes (points of no amplitude), troughs (points of minimum amplitude), or any other identical points on the wave that pass a point in a given amount of time. v is defined with units of (1/s), and λ is defined as a distance between two identical points. These quantities can be related to the speed of the wave:

\[ c= \lambda \upsilon \label{1}\]

Electromagnetic waves travel through a vacuum at the speed of light, c = 2.9979 × 108 m s–1. Since this speed a vacuum is always the same, radiation may be characterized by specifying either λ or v. The other quantity can always be calculated from Eq. \(\ref{1}\).

Further mathematical aspects of a wave can be shown in interference, when two waves interact with each other. In constructive interference, their crests coincide, their amplitudes combine, essentially creating a wave with higher magnitude. When the crests of one wave coincide with the troughs of another, they cancel out in destructive interference. Interference can be naturally found in thin pools of oil or bubbles, which appear to be flecked with rainbow color. Wavelengths of incoming light reflect at different depths within the film, interacting with each other constructively to produce the colored bands and destructively to produce the darker bands^[1]. Certain headphones emit waves of a frequency that destructively interfere with those of outside noise, and as such the headphones are dubbed "noise-canceling".

Figure \(\PageIndex{1}\) Patterns of wave interference in bubbles.

Let's go back to the automatic door issue for now. Much like the "invisible", red-colored beams of light shown guarding valubles in movies, Optical Triangulation Sensors utilize non-visible electromagnetic radiation to sense the presence of humans and automatically close or open doors. Usually a microwave beam is channeled from a LED on the hinge of the door, which reflects off of the floor in a perfect angle to reach a light-sensing object called a photodiode^[2]. When this microwave angle is interrupted, say by a passing person, a different diode receives the microwaves, sending a signal to the door sensor.

The same, subtle beam of electromagnetic radiation is found in remote control sensors. In simple TV remote controls, the remote emits infrared light which is picked up by a sensor on the television. Advanced sensors can send out wavelengths of different frequencies, allowing for multiple sensor tuning. It may seem like the beam of a remote control is resilient in reaching its sensor, even when a rude person is blocking the screen; this is just due to refraction of the waves, which may eventually reach the sensor anyway. Mirrors, however, will reflect the infrared ray.

Our enjoyment of music and media is also dependant on electromagnetic radiation; one example is with familiar CDs and other media-containing discs. Despite their smooth appearances, the surfaces of CDs and DVDs actually have thousands of miniscule bumps, which form a single ring pattern that spirals around the entire CD. A CD player works by shining a laser through a series of lenses which focus electromagnetic radiation on the gap between bumps on the CD. As the disc spins, the ray of radiation passes over tiny differences in elevation, which alters the the wavelengths of the reflected waves. These waves pass back through the system of lenses, which are refracted in a different direction and in turn alter an electrical current that is "read" to produce sound^[3].

Figure \(\PageIndex{1}\) Layers of a CD; B is the grooved surface against which electromagnetic radiation is bounced off, and E is the laser diode.

The type of radiation emitted by the laser diode is very important in determining the capacity of the disc. CDs, DVDs, and Blu-Ray discs are all essentially made up of the same silicon base material. The difference lies mostly in the gaps between bumps on the disc, which must be wide enough to accomodate the wavelengths of the incoming light beam. In order to read discs, CD players use infrared light, which means the spaces on the CD must be far apart enough to allow for infrared's relatively large wavelength. DVD players improve on this concept by relying on visible red light, which has a shorter wavelength than infrared. As a result, the grooves on a DVD are not as wide, allowing for more data to be encoded on a DVD disc. Blu-Ray discs go even further by utilizing - guess what? - blue visible light, which has an even shorter wavelength. With the advance of electronic technology in today's society, it might not be long before we start seeing Violet-Ray discs popping up at a retailer near you.

From CoreChem: 21.1: The Nature of Electromagnetic Radiation

References

1. ↑ http://electron9.phys.utk.edu/optics421/modules/m5/Interference.htm
2. ↑ archives.sensorsmag.com/artic...0598/index.htm
3. ↑ ecow2.engr.wisc.edu/courses/mod/resource/view.php?id=13637

Contributors and Attributions

• Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.