Sorting Recyclable Plastics by Density
- Page ID
- 50006
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In 2006 the amount of plastic bottles recycled reached a record high of 2,220,000,000 pounds. The amount of PET bottles recycled in 2006 increased more than 102 million pounds compared to 2005.

HDPE bottle recycling increased in 2005 to 928 million pounds. Over 18,000 million pounds is produced. All plastic bottles were recycled at a rate of 24 percent in 2005 [1]. When different plastics are melted together, they tend to fractionate like oil and water, so the products that are made from recycled plastics tend to be structurally unsound unless the plastics are carefully sorted. The sorting is done by floatation in many commercial firms. Heavy plastics sink in a brine (salt) solution, while the lighter ones float and can be separated. Different brine solutions can be ued to separate all the major plastics[2]. Surprisingly, many recyclers depend on cheap labor to sort plastics by hand, and polypropylene, which is hard for laborers to recognize, is not recycled effectively (of over 19,000 million pounds produced, only about 132 million is recycled. Polypropylene is used in multicolored margarine and yogurt tubs, for example. The terms heavy and light are commonly used in two different ways. We refer to weight when we say that an adult is heavier than a child. On the other hand, something else is alluded to when we say that polyvinyl chloride (PVC) is heavier than polypropylene (PP). A small shaving of PVC would obviously weigh less than a roomful of PP, but PVC is heavier in the sense that a piece of given size weighs more than the same-size piece of PP.
What we are actually comparing is the mass per unit volume, that is, the density. In order to determine these densities, we might weigh a cubic centimeter of each type of plastic. If the PVC sample weighed 1.40 g and the PP 0.91 g, we could describe the density of PVC as 1.40 g cm–3 and that of PP as 0.91 g cm–3. (Note that the negative exponent in the units cubic centimeters indicates a reciprocal. Thus 1 cm–3 = 1/cm3 and the units for our densities could be written as 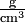 , g/cm3, or g cm–3. In each case the units are read as grams per cubic centimeter, the per indicating division.) We often abbreviate "cm3" as "cc", and 1 cm3 = 1 mL exactly by definition.
, g/cm3, or g cm–3. In each case the units are read as grams per cubic centimeter, the per indicating division.) We often abbreviate "cm3" as "cc", and 1 cm3 = 1 mL exactly by definition.
| Plastic Symbol | name | Density/g/cm3 | Uses |
|---|---|---|---|
 |
Polypropylene | 0.90 - 0.92 | yogurt cups, plasticware |
 |
Low Density Polyethylene | 0.91 - 0.93 | squeezable bottles |
 |
High Density Polyethylene | 0.94 - 0.96 | milk bottles, bags |
 |
Polystyrene | 1.03 - 1.06 | egg cartons, packing peanuts |
 |
Polyethylene Terephthalate | 1.35 - 1.38 | water bottles |
 |
Polyvinyl Chloride | 1.32 - 1.42 | juice bottles, cling wrap |
 |
Often Polycarbonate or Acrylonitrile butadiene styrene (ABS) |
1.3 1.06 |
bottles auto body parts |
| Densities of many more materials are easily found. |
There are scores of plastics in common use, each with unique Properties.
In general it is not necessary to weigh exactly 1 cm3 of a material in order to determine its density. We simply measure mass and volume and divide volume into mass:
\[\text{Density} = \dfrac{\text{mass}} {\text{volume}}\]
or
\[\rho = \dfrac{\text{m}} {\text{V}}\]
where ρ = density m = mass V = volume
Example \(\PageIndex{1}\): Density Calculation
Calculate the density of (a) a piece of PVC whose mass is 19.46 g and which, when submerged, increases the water level in a graduated cylinder by 13.9 ml; (b) a PVC cylinder of mass 12.990 g, radius 0.750 cm, and height 5.25 cm.
Solution
a) Since the submerged metal displaces its own volume,
\(\text{Density} =\rho = \dfrac{\text{m}} {\text{V}} = \dfrac{19.46 g} {13.9 mL} = \text {1.4 g/mL or 1.4 g mL}^{-1}\)
b) The volume of the cylinder must be calculated first, using the formula
\(\text{V} = {\pi} r^{2} h = 3.142 × \text{(0.750 cm)}^{2} * 5.25 \text{cm} = \text{9.278 718 8 cm}^{3}\)
Then \(\rho = \dfrac{\text{m}} {\text{V}} = \dfrac{12.990g} {9.278 718 8cm^{3}}\)
= \(\text{1.430} \dfrac{\text{g}}{\text{cm}^3}\)
Note
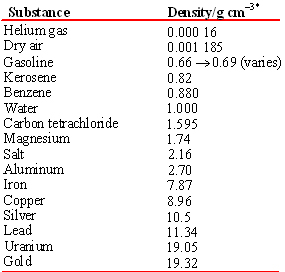
Note that unlike mass or volume, the density of a substance is independent of the size of the sample. Thus density is a property by which one substance can be distinguished from another. A sample of PVC can be trimmed to any desired volume or adjusted to have any mass we choose, but its density will always be 1.40 g/cm3 at 20°C. The densities of some common pure substances are listed in the Table.
Tables and graphs are designed to provide a maximum of information in a minimum of space. When a physical quantity (number × units) is involved, it is wasteful to keep repeating the same units. Therefore it is conventional to use pure numbers in a table or along the axes of a graph. A pure number can be obtained from a quantity if we divide by appropriate units. For example, when divided by the units gram per cubic centimeter, the density of aluminum becomes a pure number 2.70:
\[\dfrac{\text{Density of aluminum}} {\text{1 g cm}^{-3}} = \dfrac{\text{2.70 g cm}^{-3}} {\text{1 g cm}^{-3}} = 2.70\]
Table \(\PageIndex{2}\) Density of Several Substances at 20°C.
Therefore, a column in a table or the axis of a graph is conveniently labeled in the following form:
\[\dfrac{\text{Quantity}}{\text{units}}\]
This indicates the units that must be divided into the quantity to yield the pure number in the table or on the axis. This has been done in the second column of the Table.
Converting Densities
In our exploration of Density, notice that chemists may express densities differently depending on the subject. The density of pure substances may be expressed in kg/m3 in some journals which insist on strict compliance with SI units; densities of soils may be expressed in lb/ft3 in some agricultural or geological tables; the density of a cell may be expressed in mg/µL; and other units are in common use. It is easy to transform densities from one set of units to another, by multiplying the original quantity by one or more unity factors:
Example \(\PageIndex{2}\): Density Conversion
Convert the density of water, 1 g/cm3 to (a) lb/cm3 and (b) lb/ft3
a. The equality 454 g = 1 lb can be used to write two unity factors,
\(\dfrac{\text{454 g}} {\text{1 lb}}\) or \(\dfrac{\text{1 lb}} {\text{454}}\)
The given density can be multiplied by one of the unity factors to get the desired result. The correct conversion factor is chosen so that the units cancel:
\(\dfrac{\text{1 g}} {\text{cm}^{3}}* \dfrac{\text{1 lb}} {\text{454 g}} = 0.002203 \dfrac{\text{lb}} {\text{cm}^{3}}\)
b. Similarly, the equalities 2.54 cm = 1 inch, and 12 inches = 1 ft can be use to write the unity factors:
\(\dfrac{\text{2.54 cm}} {\text{1 in}}\), \(\dfrac{\text{1 in}} {\text{2.54 cm}}\), \(\dfrac{\text{12 in}} {\text{1 ft}}\) and \(\dfrac{\text{1 ft}} {\text{12 in}}\)
In order to convert the cm3 in the denominator of 0.002203 \(\dfrac{lb} {cm^{3}}\) to in3, we need to multiply by the appropriate unity factor three times, or by the cube of the unity factor:
\(\text{0.002203} \dfrac{\text{g}} {\text{cm}^{3}}\) x \(\dfrac{\text{2.54 cm}} {\text{1 in}}\) x \(\dfrac{\text{2.54 cm}} {\text{1 in}}\) x \(\dfrac{\text{2.54 cm}} {\text{1 in}}\)
or
\(\text{0.002203)} \dfrac{\text{g}} {\text{cm}^{3}}\) x \((\dfrac{\text{2.54 cm}} {\text{1 in}})^{3} = \text{0.0361} \dfrac{\text{lb}}{\text{in}^3}\)
This can then be converted to lb/ft3:
\(\text{0.0361} \dfrac{\text{lb}} {\text{in}^{3}}\) x \((\dfrac{\text{12 in}} {\text{1 ft}})^{3} = \text{62.4}\dfrac{\text{lb}}{\text{ft}^3}\)
Note
It is important to notice that we have used conversion factors to convert from one unit to another unit of the same parameter
From ChemPRIME: 1.8: Density
References
Contributors and Attributions
Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.


