Synthetic Sweeteners

Ever wonder why synthetic high-fructose corn syrup (HFCS) now shows up as an ingredient in food, but sugar almost never does? High-fructose corn syrup (HFCS) was first produced and introduced into the United States in 1968, because HFCS is less expensive to manufacture than sucrose^[2]. In 1982, the U.S. government imposed quotas that limit sugar imports. This led to big increases in U.S. sugar prices, so HFCS has displaced sugar in many foods. In the United States two classes of HFCS are manufactured, HFCS-42 and HFCS-90, which contain 42 and 90% fructose, respectively, but the two are combined to make HFCS-55. HFCS-55 has been cheaper on a comparable basis—it contains about 23% water—than sugar in the U.S. Recently, the price of sugar has declined slightly, and some people strongly prefer sugar, so some soft drinks were briefly introduced (April-June 2009) that contained sugar^[3], and one Dr Pepper bottler in Dublin, Texas, still uses sugar ( "Dublin Dr Pepper" over the Internet). There are also gourmet or local brands such as Jones Soda or Royal Crown Draft that use pure cane sugar. Recently, HFCS has been implicated in bee disease.

Cornstarch, is a polymer of glucose molecules (C₁₂H₂₂O₁₁)_n with the structure shown below. To make HFCS, cornstarch is "hydrolyzed" (allowed to react with water) with a glucoamylase catalyst to give glucose. The glucose is then partially converted enzymatically to a mixture of fructose and glucose. Fructose is an isomer of glucose, which differs only by the position of one of the =O atom. Fructose and Glucose both exist in the cyclic and open chain forms shown below.

\[\ce{C12H22O11_n ->2n C6H12O6 -> C6H12O6 + C6H12O6}\nonumber\]

glucoamylase glucose isomerase

Figure \(\PageIndex{1}\) Starch

Figure \(\PageIndex{2}\) Glucose

Figure \(\PageIndex{3}\) Fructose

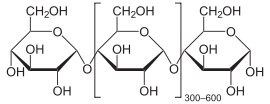
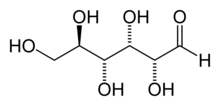
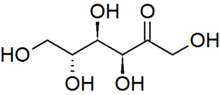
It is not unusual to obtain a mixture of two or more products, and in these cases (as with HFCS), we usually want to know the percent yield of the products.

In other cases, even though none of the reactants is completely consumed, no further increase in the amounts of the products occurs. We say that such a reaction does not go to completion. When a mixture of products is produced or a reaction does not go to completion, the effectiveness of the reaction is usually evaluated in terms of percent yield of the desired product. A theoretical yield is calculated by assuming that all the limiting reagent is converted to product. The experimentally determined mass of product is then compared to the theoretical yield and expressed as a percentage:

\[\text{Percent yield}=\dfrac{\text{actual yield}}{\text{theoretical yield}}\times \text{100 percent}\]

Example \(\PageIndex{1}\): Percent Yield

When 100.0 g (C₁₂H₂₂O₁₁)_n is allowed to react enzymatically with 20 g water, then treated glucose isomerase, 28.96 g fructose and 33.89 g of glucose are produced. Calculate the percent yield of fructose. For the purpose of this exercise, we can simplify the formula for starch by using its structural unit, sucrose, and write the overall equation

\(\ce{C12H22O11 + H2O -> C6H12O6 (fructose) + C6H12O6 (glucose)}\)

Solution We must calculate the theoretical yield of fructose, and to do this, we must first discover whether sucrose or H₂O is the limiting reagent. For the balanced equation

the stoichiometric ratio of the reactants is

\(\text{S}\dfrac{\text{H}_2\text{O}}{\text{sucrose}} = \dfrac{\text{1 mol H}_2\text{O}}{\text{1 mol sucrose}}\)

Now, the initial amounts of the two reagents are

\( n_{H_2O} (initial) = \text{20.0 g H}_2 \text{O} \times \dfrac{\text{1 mol H}_2\text{O}}{\text{18.016 g H}_2\text{O}} = \text{1.1 mol H}_2\text{O}\)

and

\( n_{sucrose} (initial) = \text{100.0 g sucrose} \times \dfrac{\text{1 mol sucrose}}{\text{342.3 g H}_2\text{O}} = \text{1.1 mol H}_2\text{O}\)
The ratio of initial amounts is thus

\(\dfrac{n_{H_2O} (initial)}{n_{sucrose}(initial)} = \dfrac{\text{1.11 mol H}_2\text{O}}{\text{0.292 mol sucrose}} = \dfrac{\text{3.80 mol H}_2\text{O}}{\text{1 mol sucrose}}\)

Since this ratio is greater than \(\text{S}\dfrac{\text{H}_2\text{O}}{\text{sucrose}}\), there is an excess of H₂O. Sucrose is the limiting reagent. Accordingly we must use 0.292 mol sucrose (rather than 1.11 mol H₂O) to calculate the theoretical yield of fructose. We then have

\(n_{fructose} (theoretical) = \text{0.292 mol sucrose} \times \dfrac{\text{1 mol fructose}}{\text{1 mol sucrose}} = \text{0.292 mol fructose}\)

so that

\(\text{m}_{fructose} (theoretical) = \text{0.292 mol fructose} \times \dfrac{\text{180.16 g fructose}}{\text{1 mol fructose}} = \text{52.6 g fructose}\)

The percent yield is then

\(\text{Percent yield}=\dfrac{\text{actual yield}}{\text{theoretical yield}}\times \text{100 percent} = \dfrac{\text{28.96 g}}{\text{52.6}} \times \text{100 percent} = \text{55.05 percent}\)

In order to make HFCS, a chemist would have to continuously monitor the products until the ratio of fructose to glucose is at the desired level. In this case, not all of the sucrose (or starch that it represents) has been converted to glucose and sucrose, because if it had, the total mass of products would be over 100 g (the mass of sugar + the mass of water that reacts (0.292 mol x 18 g/mol, or 5.25 g) or 105.25 g. It's only 28.96 + 33.89 = 62.85 g.

From ChemPRIME: 3.3: Percent Yield

Contributors and Attributions

• Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.