Low Density Lipoproteins

High-density lipoproteins (HDL^[1]) form a class of lipoproteins, varying somewhat in their size (8–11 nm in diameter), that carry fatty acids and cholesterol from the body's tissues to the liver, where they are recycled or excreted. This is the main reason why HDL-bound cholesterol is sometimes called "good cholesterol", or HDL-C. About thirty percent of blood cholesterol is carried by HDL ^[2]. Fatty ("hydrophobic") substances like cholesterol and triglycerides (animal fats) would not be soluble in blood without lipoproteins, which form soap-like miscelles with hydrophilic (water-bonding ) groups like "apolipoproteins" that solubilize fats in blood plasma.

Figure $\PageIndex{1}$: Lipoprotein structure (chylomicron) ApoA, ApoB, ApoC, ApoE (apolipoproteins); T (triacylglycerol); C (cholesterol); orange (phospholipids)^[3] from OpenStax College (CC-SA-3.0)

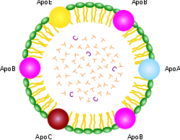
In contrast to HDL-C, "bad" Low Density Lipoprotein (LDL)carries cholesterol from the digestive track throughout the body. At higher concentrations, it may coat and constrict blood vessels (atherosclerosis), especially in people who eat a lot of carbohydrates or drink alcohol chronically. Both HDLs and LDLs are actually "heavier" than water, which is surprising for a lipid, or oil. This is due to their significant protein content. The terms heavy and light are commonly used in two different ways. We refer to weight when we say that an adult is heavier than a child. On the other hand, something else is alluded to when we say that water is heavier than vegetable oil. A drop of water would obviously weigh less than a gallon of oil, but water is heavier in the sense that a sample of given size weighs more than the same-size sample of oil.

What we are actually comparing is the mass per unit volume, that is, the density. In order to determine these densities, we might weigh a cubic centimeter of each liquid. If the water sample weighed 0.998 g and the oil 0.91 g, we could describe the density of water as 0.998 g cm^–3 and that of oil 0.91 g cm^–3. (Note that the negative exponent in the units cubic centimeters indicates a reciprocal. Thus 1 cm^–3 = 1/cm³ and the units for our densities could be written as g/cm³, or g cm^–3. In each case the units are read as grams per cubic centimeter, the per indicating division.) We often abbreviate "cm³" as "cc", and 1 cm³ = 1 mL exactly, by definition.

In general it is not necessary to weigh exactly 1 cm³ of a material in order to determine its density. We simply measure mass and volume and divide volume into mass:

$$\text{Density} = \dfrac{\text{mass}} {\text{volume}}$$

or

$$\rho = \dfrac{\text{m}} {\text{V}}$$

where

• ρ = density
• m = mass
• V = volume

Example $\PageIndex{1}$: Density Calculation

Calculate the density of (a) a sample of oil whose mass is 11.12 g and which fills a graduated cylinder 1to 13.9 ml; (b) a sample of HDL of mass 7.89 g, in a cylindrical dish of radius 0.750 cm, and height 5.25 cm.

Solution

a) $$\text{Density} =\rho = \dfrac{\text{m}} {\text{V}} = \dfrac{\text{11.12 g}} {\text{13.9 mL}} = \text {0.9 g/mL or 0.9 g mL}^{-1}$$

b) The volume of the cylinder must be calculated first, using the formula

$$\text{V} = {\pi} r^{2} h = 3.142 × \text{(0.750 cm)}^{2} * 5.25 \text{cm} = \text{9.278 718 8 cm}^{3}$$

Then

$$\rho = \dfrac{\text{m}} {\text{V}} = \dfrac{\text{7.89 g}} {\text{9.278 718 8 cm}^{3}} = 0.85 \dfrac{\text{g}} {\text{cm}^{3}}$$

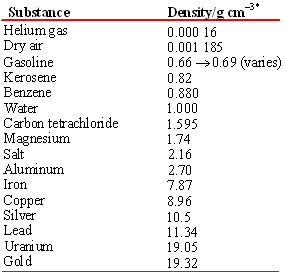
Note that unlike mass or volume, the density of a substance is independent of the size of the sample. Thus density is a property by which one substance can be distinguished from another. Any size sample of pure vegetable oil can be divided into any desired volume or adjusted to have any mass we choose, but its density will always be 0.80 g/cm³ at 20°C. The densities of some common pure substances are listed below^[4]:

Table $\PageIndex{1}$: Densities of Common Substances

Density /g/cm^3	Class	Diameter (nm)	% protein	% cholesterol	% phospholipid	% triacylglycerol
>1.063	HDL	5-15	33	30	29	8
1.019-1.063	LDL	18-28	25	50	21	4
1.006-1.019	Intermediate density lipoprotein (IDL)	25-50	18	29	22	31
0.95-1.006	VLDL	30-80	10	22	18	50
<0.95	Chylomicrons	100-1000	<2	8	7	84

Densities of many more materials are easily found.

Tables and graphs are designed to provide a maximum of information in a minimum of space. When a physical quantity (number × units) is involved, it is wasteful to keep repeating the same units. Therefore it is conventional to use pure numbers in a table or along the axes of a graph. A pure number can be obtained from a quantity if we divide by appropriate units. For example, when divided by the units gram per cubic centimeter, the density of a HDL becomes a pure number 1.063:

$$\dfrac{\text{Density of HDL}} {\text{1 g cm}^{-3}} = \dfrac{\text{1.063 g cm}^{-3}} {\text{1 g cm}^{-3}} = 1.063$$

Density of Several Substances at 20°C.

Therefore, a column in a table or the axis of a graph is conveniently labeled in the following form:

$$\dfrac{\text{Quantity}}{\text{units}}$$

This indicates the units that must be divided into the quantity to yield the pure number in the table or on the axis. This has been done in the second column of the Tables.

The density of lipoproteins can be determined by untracentrifugation of a mixture which forms a density gradient, with the most dense layers near the bottom, and the most dense layers at the top. The lipoproteins can be visualized with dyes, and the percentages of the various lipoproteins can be used diagnostically. The layers look like this model made from sugar solutions:

Figure $\PageIndex{2}$: Density Gradient made from colored sugar water (16%, 12%, 8%, 4%.)

Converting Densities

In our exploration of Density, notice that chemists may express densities differently depending on the subject. The density of pure substances may be expressed in kg/m³ in some journals which insist on strict compliance with SI units; densities of soils may be expressed in lb/ft³ in some agricultural or geological tables; the density of a cell may be expressed in mg/µL; and other units are in common use. It is easy to transform densities from one set of units to another, by multiplying the original quantity by one or more unity factors:

Example $\PageIndex{2}$ : Density Conversion

Convert the density of water, 1 g/cm³ to (a) lb/cm³ and (b) lb/ft³

a. The equality 454 g = 1 lb can be used to write two unity factors,

$\dfrac{\text{454 g}} {\text{1 lb}}$ or $\dfrac{\text{1 lb}} {454}$

The given density can be multiplied by one of the unity factors to get the desired result. The correct conversion factor is chosen so that the units cancel:

$\dfrac{\text{1 g}} {\text{cm}^{3}}* \dfrac{\text{1 lb}} {\text{454 g}} = 0.002203 \dfrac{\text{lb}} {\text{cm}^{3}}$

b. Similarly, the equalities 2.54 cm = 1 inch, and 12 inches = 1 ft can be use to write the unity factors:

$\dfrac{2.54 cm} {1in}$, $\dfrac{1 in} {2.54 cm}$, $\dfrac{12 in} {1ft}$ and $\dfrac{1ft} {12in}$

In order to convert the cm³ in the denominator of 0.002203 $\dfrac{\text{lb}} {\text{cm}^{3}}$ to in³, we need to multiply by the appropriate unity factor three times, or by the cube of the unity factor:

$\text{0.002203} \dfrac{\text{g}} {\text{cm}^{3}}$ x $\dfrac{\text{2.54 cm}} {\text{1in}}$ x $\dfrac{\text{2.54 cm}} {\text{1in}}$ x $\dfrac{\text{2.54 cm}} {\text{1in}}$

or

$\text{0.002203} \dfrac{\text{g}} {\text{cm}^{3}}$ x $(\dfrac{\text{2.54 cm}} {\text{1in}})^{3} = \text{0.0361} \dfrac{\text{lb}}{\text{in}^3}$

This can then be converted to lb/ft³:

$\text{0.0361} \dfrac{lb} {in^{3}}$ x $(\dfrac{12 in} {1ft})^{3} = \text{62.4} \dfrac{\text{lb}}{\text{ft}^3}$

Note

It is important to notice that we have used conversion factors to convert from one unit to another unit of the same paramter

From ChemPRIME: 1.8: Density

References

1. en.Wikipedia.org/wiki/High_density_lipoprotein
2. en.Wikipedia.org/wiki/High_density_lipoprotein#cite_note-am180-0
3. en.Wikipedia.org/wiki/Lipoprotein
4. Biochemistry 2nd Ed. 1995 Garrett & Grisham

Contributors and Attributions

• Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.