Frog Legs to Electron Transport

What could be in a chapter called "The Electron" for biologists?

Well, in order to understand metabolism and how our body actually derives energy from food and air, or to understand photosynthesis, it's necessary to understand the |electron transport chain. Energy is released when positive nuclei and negative electrons get closer together through bond formation or "Redox" reactions, just as potential energy is released when heavy objects fall towards Earth. Understanding the nature of the electron is critical to understanding these energy-producing processes.

Luigi Galvani

Figure \(\PageIndex{1}\) Late 1780s diagram of Galvani's experiment on frog legs.^[1]

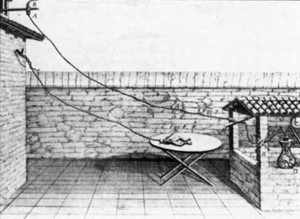
The connection between electricity (movement of electrons) and biology was established early on, when Luigi Galvani, around 1780, wired a frog to a metal railing, hoping to see the effects of a lightning strike. He observed wild twitching of the frog's legs, with or without lightning. He had discovered (unknowingly) the generation of electrical current by Galvanic Cells (named after Galvani), and the electrical nature of nerve stimulation of muscles.

Michael Faraday

Near the middle of the nineteenth century the English chemist and physicist Michael Faraday (1791 to 1867) established a connection between electricity and chemical reactions. He already knew that an electric current flowing into certain molten compounds through metal plates called electrodes could cause reactions to occur. Humphrey Davy had shown that samples of different elements would deposit on the electrodes. Faraday found that the same quantity of electric charge was required to produce 1 mol of any element whose valence was 1. Twice that quantity of charge would deposit 1 mol of an element whose valence was 2, and so on. Electric charge is measured in units called coulombs, abbreviated C. One coulomb is the quantity of charge which corresponds to a current of one ampere flowing for one second. It was found that 96500 C of charge was required to deposit on an electrode l mol of an element whose valence is l.

Faraday’s experiments strongly suggested that electricity, like matter, consists of very small indivisible particles. The name electron was given to these particles, and an electric current came to be thought of as a flow of electrons from one place to another. When such a current flows into a chemical compound, one electron is required for each atom of a univalent element deposited on an electrode, two electrons for each atom of an element whose valence is 2, and so on. Thus an electric charge of 96500 C corresponds to 1 mol of indivisible electric particles (electrons).

The relationship between electricity and atomic structure was further clarified by experiments involving cathode-ray tubes in the 1890s.

Figure \(\PageIndex{2}\) Crookes Cathode Ray Tube ^[2]

J.J. Thompson and the Crookes Tube

Around 1870, William Crookes developed a "cathode-ray tube" by pumping most of the air or other gas out of a glass tube and applying a high voltage to two metal electrodes inside. There are videos on YouTube of classroom demonstrations and homemade cathode ray tubes. Early cathode ray tubes were called "Crookes Tubes" in honor of their inventor. If ZnS or some other phosphor is placed on the glass at the end of the tube opposite the negatively charged electrode (cathode), the ZnS emits light. This indicates that some kind of rays are streaming away from the cathode. In 1897, the English physicist J. J. Thomson showed that when the cathode ray tube is placed between the poles of a magnet, the cathode rays are deflected the same way as the β particles described earlier. The fact that they were very small electrically charged particles led (1856 to 1940) to identify them with the electrons of Faraday’s experiments. Thus cathode rays are a beam of electrons which come out of the solid metal of the cathode. They behave exactly the same way no matter what the electrode is made of or what gas is in the tube. These observations allow one to conclude that electrons must be constituents of all matter. In addition to being deflected by a magnet, the electron beam in a cathode-ray tube can be attracted toward a positively charged metal plate or repelled from a negative plate. By adjusting such electrodes to exactly cancel the deflection produced by a magnet of known strength, Thomson was able to determine that the ratio of charge to mass for an electron is 1.76 × 10⁸ C/g. This is a rather large ratio. Either each electron has a very large charge, or each has a very small mass. We can see which by using Faraday’s result that there are 96 500 C mol^–1 of electrons

\[\dfrac{\text{96 500 C mol}^{-\text{1}}}{\text{1}\text{.76 }\times \text{ 10}^{\text{8}}\text{ C g}^{-\text{1}}}=\text{5}\text{.48 }\times \text{ 10}^{-\text{4}}\text{ g mol}^{-\text{1}}\]

Thus the molar mass of an electron is 5.48 × 10^–4 g mol^–1, and if we think of the electron as an “atom“(or indivisible particle) of electricity, its atomic weight would be 0.000548—only \(\dfrac{1}{1837}\) that of hydrogen, the lightest element known.

Robert Millikan

In 1909 the American physicist Robert A. Millikan (1863 to 1953) was able to determine the charge on an electron independently of its mass. His value of 1.6 × 10^–19 C can be combined with Thomson’s charge-to-mass ratio to give an independent check on the molar mass for the electron

\[\dfrac{\text{1}\text{.60 }\times \text{ 10}^{-\text{19}}\text{ C}}{\text{1}\text{.76 }\times \text{ 10}^{\text{8}}\text{ C g}^{-\text{1}}}\text{ }\times \text{ 6}\text{.022 }\times \text{ 10}^{\text{23}}\text{ mol}^{-\text{1}}=\text{5}\text{.47 }\times \text{ 10}^{-\text{4}}\text{ g mol}^{-\text{1}}\]

thus confirming that the electron has much less mass than the lightest atom. (The quantity 1.6 × 10^–19 C is often represented by the symbol e. Thus the charge on a single electron is –e = –1.6 × 10^–19 C. The minus sign indicates that the electron is a negatively charged particle.)

In the first paragraph, we mentioned metabolism, photosynthesis, and twitching frogs' legs but it appears that we're pretty far from those topics. As a matter of fact, most biologists do not use the information on this page very often, but biologists in many areas base their understanding of what they do on what we've presented here. For example, the voltage that stimulated frogs legs must be multiplied by charge to calculate electrical potential energy, E(Joules) = q(Coulombs) x V(Joules/Coulomb). Understanding the difference between q and V, and the nature of the electron, is fundamental to understanding all the electrical processes mentioned earlier.

From ChemPRIME: 4.8: The Electron

References

1. ↑ en.Wikipedia.org/wiki/Luigi_Galvani
2. ↑ en.Wikipedia.org/wiki/Cathode_ray

Contributors and Attributions

• Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.