Carbohydrate Reactions

We have now determined symbols and formulas for many ingredients in chemical equations involving water and carbohydrates, but one important step remains. We must be sure that our equations reflect the way they occur in our bodies or our environment, where all the atoms in the reactants also appear in products. The law of conservation of mass is obeyed. The same number of atoms (or moles of atoms) of a given type must appear on each side of the equation. This reflects our belief in Dalton’s third postulate that atoms are neither created, destroyed, nor changed from one kind to another during a chemical process. When the law of conservation of mass is obeyed, the equation is said to be balanced.

As a simple example of how to balance an equation, let us take the reaction which occurs when oxygen combines with hydrogen to give the familiar substance water:

\[\ce{H2 + O2 -> H2O}\]

but it is not balanced because there are 2 oxygen atoms (in O₂) on the left side of the equation and only 1 on the right.

An incorrect way of obtaining a balanced equation is to change this to

\[\ce{H2 + O2 -> H2O2}\label{2}\]

This equation is wrong because we had already determined from the properties of the product that the product was H₂O, not H₂O₂ (which we learned earlier is used in rocket engines and can burn skin in higher concentrations). Equation \(\ref{2}\) is balanced, but it refers to a different reaction which produces a different product. The equation might also be incorrectly written as

\[\ce{H2 + O -> H2O}\]

The formula O suggests that oxygen does not exist as molecules containing 2 oxygen atoms each were involved, but we've seen in Modeling the Elements in Water that oxygen atoms do not occur alone.

In balancing an equation you must remember that the subscripts in the formulas have been determined experimentally. Changing them indicates a change in the nature of the reactants or products. It is permissible, however, to change the amounts of reactants or products involved by changing the coefficients.

For example, the first step in balancing the equation in question is as follows:

\[\ce{H2 + O2 -> 2H2O}\]

because this balances the oxygen atoms. But now there are 4 hydrogen atoms on the right, and we must complete the process by writing

\[\ce{2 H2 + O2 -> 2 H2O}\]

The 2 written before the symbol H₂ and before H₂O is called a coefficient. It indicates that on the microscopic level 2H₂ atoms are required to react with the O₂ molecule to give 2 H₂O molecules. On a macroscopic scale the coefficient 2 means that 2 mol H₂ molecules are required to react with 1 mol O₂ molecules. Twice the amount of H₂ (per O₂) is required to make H₂O as we needed for H₂O₂.

To summarize: Once the formulas (subscripts) have been determined, an equation is balanced by adjusting coefficients. Nothing else may be changed.

Example \(\PageIndex{1}\): Balance the Equation

Balance the equation for the decomposition of hydrogen peroxide:

\(\ce{H2O2 -> H2O + O2}\)

Solution Although H is balanced, O is not. We notice that oxygen atoms come in pairs on the left, but there's an odd number on the right. The only way to fix that is to add a coefficient of 2 before H₂O:

\(\ce{H2O2 -> 2H2O + O2}\)

Now H is not balanced. We need 2 H₂O₂ molecules on the left to balance H, and luckily balance the 4 O on the right:

\(\ce{2H2O2 -> 2H2O + O2}\)

We now have 4 H atoms and 4 O atoms on each side, and so balancing is complete.

Most chemists use several techniques for balancing equations ^[1] For example, it helps to know which element you should balance first. When each chemical symbol appears in a single formula on each side of the equation you can start wherever you want and the process will work. When a symbol appears in three or more formulas, however, that particular element will be more difficult to balance and should usually be left until last.

Example \(\PageIndex{2}\): Balanced Equation for a Reaction

When sucrose (C₁₂H₂₂O₁₁) is metabolized in the body, the overall reaction requires oxygen and yields only carbon dioxide (CO₂) and water. Write a balanced equation to describe this reaction. [Note: this is called an overall reaction, because the actual mechanism is much more complex. The process starts by breaking sucrose into glucose and fuctose in saliva, and continues in a complex process to convert those simple sugars to carbon dioxide and water].

Solution First write an unbalanced equation showing the correct formulas of all the reactants and products:

\(\ce{C12H22O11 + O2 -> CO2 + H2O}\)

We note that O atoms appear in four formulas, two on the left and two on the right. Therefore we balance C and H first. The formula C₁₂H₂₂O₁₁ determines how many C and H atoms must remain after the reaction, and so we write coefficients of 12 for CO₂ and 11 for H₂O:

\(\ce{C12H22O11 + O2 -> 12 CO2 + 11 H2O}\)

We now have a total of 35 O atoms on the right-hand side, and the equation can be balanced by using a coefficient of \(\dfrac{35}{2}\) in front of O₂:

\(\ce{C12H22O11 + 35/2 O2 -> 12 CO2 + 11 H2O}\)

Usually it is preferable to remove fractional coefficients since they might be interpreted to mean a fraction of a molecule. (One-half of an O₂ molecule would be an O atom, which, as we've seen, does not exist except at very high temperatures.) Therefore we multiply all coefficients on both sides of the equation by two to obtain the final result:

\(\ce{2 C12H22O11 + 35 O2 -> 24 CO2 + 22 H2O}\)

(Sometimes, when we are interested in moles rather than individual molecules, it may be useful to omit this last step. Obviously the idea of half a mole of O₂ molecules, that is, 3.011 × 10²³ molecules, is much more tenable than the idea of half a molecule.)

Another useful technique is illustrated in Example 2. When an element (such as O₂) appears by itself, it is usually best to choose its coefficient last. Furthermore, groups such as NO₃, SO₄, etc., often remain unchanged in a reaction and can be treated as if they consisted of a single atom. When such a group of atoms is enclosed in parentheses followed by a subscript, the subscript applies to all of them. That is, the formula involves Ca(NO₃)₂ involves 1Ca, 2N and 2 × 3 = 6 O atoms.

Example \(\PageIndex{3}\): Tollens Test Part 1

You may be familiar with the Tollens Test, which gives a silver mirror on a test tube when tollens reagent is added to simple (reducing) sugars like glucose (but not polysaccharides like sucrose). Tollens Reagent is made by first adding sodium hydroxide to an aqueous (water) solution of silver nitrate, to give a brown precipitate of silver oxide. The overall unbalanced equation for the first step in the preparation of Tollens Reagent is

\(\ce{AgNO3 (aq) + NaOH (aq) -> NaNO3 + Ag2O + H2O}\)

Balance this equation.

Solution We note that oxygen atoms are found in every one of the five formulas in the equation, making it especially hard to balance. However, Ag appears only in two formulas:

\(\ce{2 AgNO3 (aq) + NaOH (aq) -> NaNO3 + Ag2O + H2O}\)

That gives us two nitrate ions (NO₃^-) on the left, which we can easily balance:

\(\ce{2 AgNO3 (aq) + NaOH (aq) -> 2NaNO3 + Ag2O + H2O}\)

Now we can balance the sodium, Na:

\(\ce{2AgNO3 (aq) + 2NaOH (aq) -> 2NaNO3 + Ag2O + H2O}\)

Now, since we've balance the nitrate ions, we can focus on just the hydrogen and oxygen not in nitrate, and find that there are 2 O and 2 H in the 2 hydroxide ions (OH^-) on the left, and 2 O (in Ag₂O and H₂O) and 2 H (in H₂O) on the right, so it's balanced!

Example \(\PageIndex{4}\): Tollens Test Part 2

The second step in the synthesis of Tollens Reagent involves adding concentrated ammonia (NH₃) until the brown silver oxide dissolves, according to the unbalanced equation

\(\ce{Ag2O (s) + NH3 (aq) + NaNO3 (aq) + H2O (l) -> Ag(NH3)2NO3 (aq) + NaOH (aq)}\)

Balance this equation.

Tollens reagent cannot be stored because it becomes explosive, as the silver diammine complex, with two uncharged NH3 groups attached to a Ag+ ion

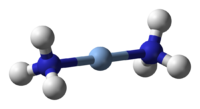
the diamminesilver complex, with a 1+ charge^[2] degrades to the contact explosive silver fulminate.

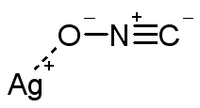
Silver Fulminate^[3]

Solution Once more, start with the Ag which appears only once on each side:

\(\ce{Ag2O (s) + NH3 (aq) + NaNO3 (aq) + H2O (l) -> 2Ag(NH3)2NO3 (aq) + NaOH (aq)}\)

Now we need 4 NH₃ and 2 NO₃ on the left:

\(\ce{Ag2O (s) + 4 NH3 (aq) + 2 NaNO3 (aq) + H2O (l) -> 2 Ag(NH3)2NO3 (aq) + NaOH (aq)}\)

Finally, we need 2 Na on the right:

\(\ce{Ag2O (s) + 4 NH3 (aq) + 2 NaNO3 (aq) + H2O (l) -> 2Ag(NH3)2NO3 (aq) + 2NaOH (aq)}\)

And if we check for the oxygen that does not appear in NO , we find two of each on both sides, so the equation is balanced.

Notice that in this example we followed the rule of balancing first those elements whose symbols appeared in the smallest number of formulas: Na, Ag and NO₃) and O or H in three each. Even using this rule, however, equations in which one or more elements appear in four or more formulas are difficult to balance without some additional techniques which we will develop when we investigate reactions in aqueous solutions.

 

Example \(\PageIndex{5}\): Tollens Test Part 3

Tollens reagent reacts with simple sugars to make gluconic acid, (C₆H₁₂O₇) according to the unbalanced equation:

\(\ce{C6H12O6 + NaOH + Ag(NH3)2NO3 -> Ag + H2O + NH3 + NaNO3 + C6H12O7}\)

Gluconic acid occurs naturally fruits, honey, and wine. It is added to commercial foods as an acidity regulator. It is also used in cleaning products because it tightly bonds to metals in mineral deposits ^[4].

Solution

Note that everything seems balanced except the O, and if we focus on the O not in NO₃, we see that there is 1 on the right in H₂O, and one extra in C₆H₁₂O₇ compared to C₆H₁₂O₆. these must be balanced by adding 2 NaOH:

\(\ce{C6H12O6 + 2NaOH + Ag(NH3)2NO3 -> Ag + H2O + NH3 + NaNO3 + C6H12O7}\)

Then the two H atoms balance the H in H₂O, but we must add "2" before NaNO₃, also before Ag(NH₃)₂NO₃ to balance NO₃, then 4 before NH₃ and finally 2 before Ag:

\(\ce{C6H12O6 + 2NaOH + 2Ag(NH3)2NO3 -> 2Ag + H2O + 4NH3 + 2NaNO3 + C6H12O7}\)

From ChemPRIME: 2.12: Balancing Chemical Equations

References

1. ↑ Laurence E. Strong, Balancing Chemical Equations, Chemistry, vol. 47, no. 1, pp. 13-16, January 1974, discusses some techniques in more detail.
2. ↑ en.Wikipedia.org/wiki/Tollens%27_reagent
3. ↑ en.Wikipedia.org/wiki/Silver_fulminate
4. ↑ en.Wikipedia.org/wiki/Gluconic_acid

Contributors and Attributions

• Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.