Analysis of CHO Compounds

As we've seen, our diet includes many carbohydrates, and you might wonder if there's a way to analyze a sample to tell if it's sucrose, or one of the synthetic sweeteners like sorbitol or high fructose corn syrup, or even a compound like vitamin C, which is synthesized from sugars and like them, contains only C, H, and O. There is such a way, and it's one of the most fundamentally important forms of analysis, called elemental analysis. It's one of the first methods researchers use to identify a new compound.

Up to this point we have obtained all stoichiometric ratios from the coefficients of balanced chemical equations. Chemical formulas also indicate relative amounts of substance, however, and stoichiometric ratios may be derived from them, too. For example, the formula CO₂ tells us that no matter how large a sample of carbon dioxide we have, there will always be 2 mol of oxygen atoms for each mole of carbon atoms. That is, from the formula CO₂ we have the stoichiometric ratio

\[\large\text{S}\left( \dfrac{\text{O}}{\text{C}} \right)=\dfrac{\text{2 mol O}}{\text{1 mol C}}\]

We could also determine that for CO₂

\[\large\text{S}\left( \dfrac{\text{O}}{\text{CO}_{\text{2}}} \right)=\dfrac{\text{2 mol O}}{\text{1 mol CO}_{\text{2}}}\]

\[\large\text{S}\left( \dfrac{\text{C}}{\text{CO}_{\text{2}}} \right)=\dfrac{\text{1 mol C}}{\text{1 mol CO}_{\text{2}}}\]

(The reciprocals of these stoichiometric ratios are also valid for CO₂.)

Stoichiometric ratios derived from formulas instead of equations are involved in the most common procedure for determining the empirical formulas of compounds which contain only C, H, and O. A weighed quantity of the substance to be analyzed is placed in a combustion train and heated in a stream of dry O₂. All the H in the compound is converted to H₂O(g) which is trapped selectively in a previously weighed absorption tube. All the C is converted to CO₂(g) and this is absorbed selectively in a second tube. The increase of mass of each tube tells, respectively, how much H₂O and CO₂ were produced by combustion of the sample

Figure \(\PageIndex{1}\) A combustion train. H₂O and CO₂, produced by combination of O₂ with H and C in the sample, are selectively absorbed by tubes containing Dehydrite [Mg(ClO₄)₂•3H₂O] and ascarite (NaOH on asbestos).

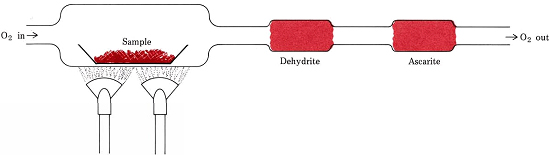
Example \(\PageIndex{1}\): Empirical Formula of Ascorbic Acid

A 6.49-mg sample of ascorbic acid (vitamin C) was burned in a combustion train. 9.74 mg CO₂ and 2.64 mg H₂O were formed. Determine the empirical formula of ascorbic acid.

Solution We need to know the amount of C, the amount of H, and the amount of O in the sample. The ratio of these gives the subscripts in the formula. The first two may be obtained from the masses of CO₂ and H₂O using the molar masses and the stoichiometric ratios

\[\large\text{S}\left( \dfrac{\text{C}}{\text{CO}_{\text{2}}} \right)=\dfrac{\text{1 mol C}}{\text{1 mol CO}_{\text{2}}}\]

\[\large\text{S}\left( \dfrac{\text{H}}{\text{H}_{\text{2}}\text{O}} \right)=\dfrac{\text{2 mol H}}{\text{1 mol H}_{\text{2}}\text{O}}\]

Thus

\[\begin{align}\large n_{\text{C}}&=\text{9}\text{.74}\times \text{10}^{\text{-3}}\text{g CO}_{\text{2}}\times \Large{\dfrac{\text{1 mol CO}_{\text{2}}}{\text{44}\text{.01 g CO}_{\text{2}}}} \large \times \Large{\dfrac{\text{1 mol C}}{\text{1 mol CO}_{\text{2}}}} \large = \text{2.21}\times \text{10}^{-4}\text{ mol C}\\ { } \\ \large n_{\text{H}} &=\text{2}\text{.64}\times \text{10}^{\text{-3}}\text{g H}_{\text{2}}\text{O}\times \Large{\dfrac{\text{1 mol H}_{\text{2}}\text{O}}{\text{18}\text{.02 g H}_{\text{2}}\text{O}}} \large \times \Large{\dfrac{\text{2 mol H}}{\text{1 mol H}_{\text{2}}\text{O}}} \large = \text{2.93}\times \text{10}^{\text{-4}}\text{ mol H} \end{align}\]

The compound may also have contained oxygen. To see if it does, calculate the masses of C and H and subtract from the total mass of sample

\[\begin{align} \large m_{\text{C}}&=\text{2}\text{.21}\times \text{10}^{\text{-4}}\text{ mol C}\times \dfrac{\text{12}\text{.01 g C}}{\text{1 mol C}}=\text{2}\text{.65}\times \text{10}^{\text{-3}}\text{g C}=\text{2}\text{.65 mg C} \\ & \\ \large m_{\text{H}}&=\text{2}\text{.93}\times \text{10}^{\text{-4}}\text{ mol H}\times \dfrac{\text{1}\text{.008 g H}}{\text{1 mol H}}=\text{2}\text{.95}\times \text{10}^{\text{-4}}\text{g H}=\text{0}\text{.295 mg H} \\ \end{align}\]

Thus we have

\[6.49 \text{mg sample} – 2.65 \text{mg C} – 0.295 \text{mg H} = 3.54 \text{mg O} \]

and

\[\large n_{\text{O}}\normalsize=\text{3}\text{.54}\times \text{10}^{\text{-3}}\text{ g O}\times \Large{\dfrac{\text{1 mol O}}{\text{16.00 g O}}} \normalsize=\text{2}\text{.21}\times \text{10}^{\text{-4}}\text{ mol O}\]

The ratios of the amounts of the elements in ascorbic acid are therefore

\[\Large{\dfrac{n_{\text{H}}}{n_{\text{C}}}=\dfrac{\text{2}\text{.93}\times \text{10}^{\text{-4}}\text{ mol H}}{\text{2}\text{.21}\times \text{10}^{\text{-4}}\text{ mol C}}=\dfrac{\text{1}\text{.33 mol H}}{\text{1 mol C}}=\dfrac{\text{1}\dfrac{1}{3}\text{mol H}}{\text{1 mol C}}=\dfrac{\text{4 mol H}}{\text{3 mol C}}}\]

\[\Large{\dfrac{n_{\text{O}}}{n_{\text{C}}}=\dfrac{\text{2}\text{.21}\times \text{10}^{\text{-4}}\text{ mol O}}{\text{2}\text{.21}\times \text{10}^{\text{-4}}\text{ mol C}}=\dfrac{\text{1 mol O}}{\text{1 mol C}}=\dfrac{\text{3 mol O}}{\text{3 mol C}}}\]

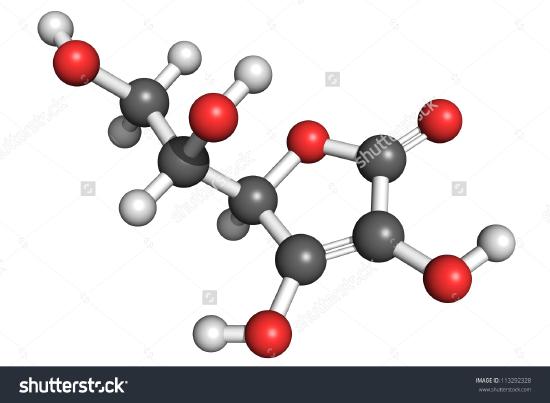
Since n_C:n_H:n_O is 3 mol C:4 mol H:3 mol O, the empirical formula is C₃H₄O₃.

A drawing of a molecule of ascorbic acid is shown here. You can determine by counting the atoms that the molecular formula is C₆H₈O₆—exactly double the empirical formula. It is also evident that there is more to know about a molecule than just how many atoms of each kind are present. In ascorbic acid, as in other molecules, the way the atoms are connected together and their arrangement in three-dimensional space are quite important. A picture showing which atoms are connected to which is called a structural formula. Empirical formulas may be obtained from percent composition or combustion-train experiments, and, if the molecular weight is known, molecular formulas may be determined from the same data. More complicated experiments are required to find structural formulas. In Example 2 we obtained the mass of O by subtracting the masses of C and H from the total mass of sample. This assumed that only C, H, and O were present. Sometimes such an assumption may be incorrect. When penicillin was first isolated and analyzed, the fact that it contained sulfur was missed. This mistake was not discovered for some time because the atomic weight of sulfur is almost exactly twice that of oxygen. Two atoms of oxygen were substituted in place of one sulfur atom in the formula.

Figure \(\PageIndex{2}\) A 3D representation of L-Ascorbic Acid ¹

From ChemPRIME: 3.4: Analysis of Compounds

References

1. http://www.shutterstock.com/pic-1132...nt-immune.html

Contributors and Attributions

• Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.