Titration of a Weak Base with a Strong Acid
- Page ID
- 368
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Data obtained through the process of titration can be used to compute the molarity and the correlated acidity of a solution at various times of the titration. The initial and final volumes of the analyte and titrant solutions, as well as the pH, or measure of acidity, are essential in calculating the total number of moles of analyte present. Once this information is determined, the molarity of the analyte, which was unknown before the titration, can then be computed, because its volume was measured beforehand. However, chemists are often interested in the data collected at various points during the titration as well, not just at the beginning and the end. These data can then be translated to points on a graph, resulting in an informational titration curve.
Introduction
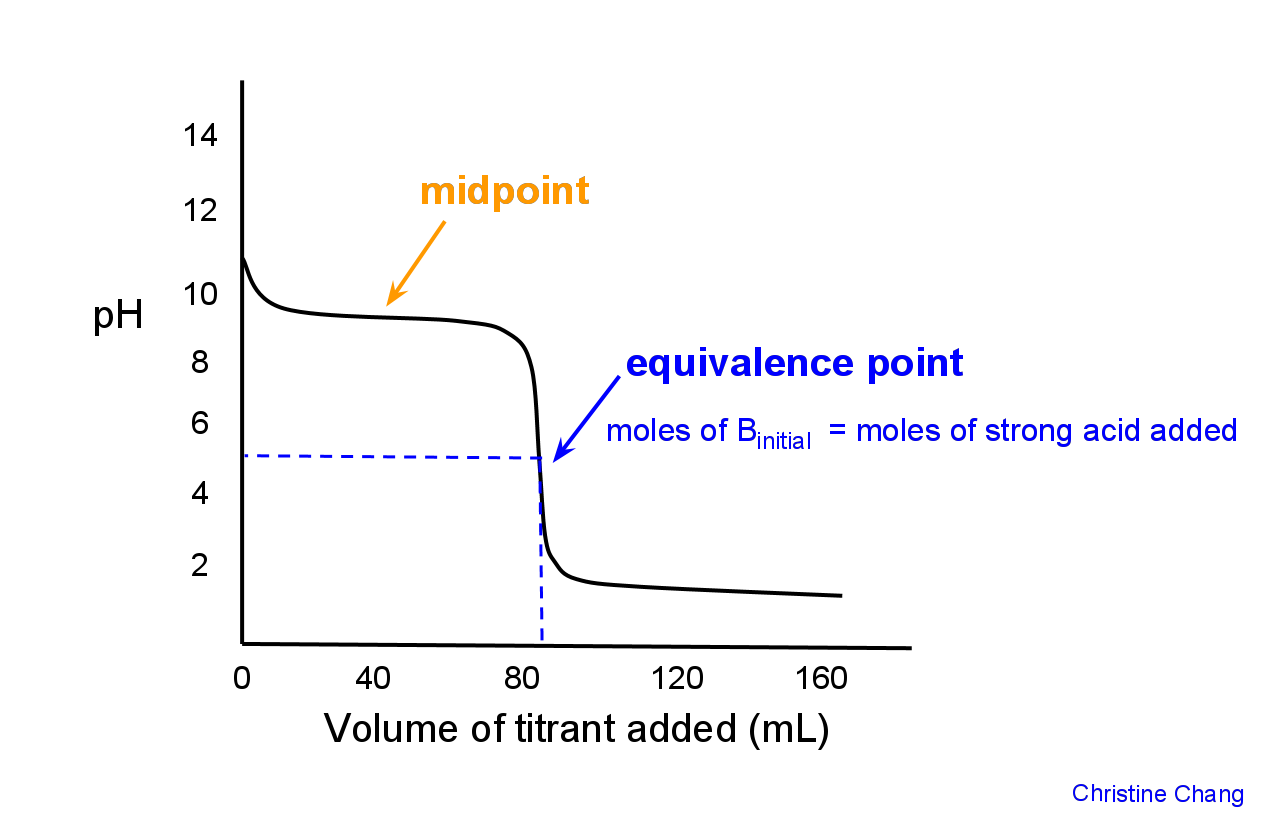
Chemists are typically interested in calculating volume and acidity data for the following critical points: at the starting point before any titrant is added, at the midpoint, at a point before the equivalence point (excluding the initial condition), at the equivalence point, and past the equivalence point.
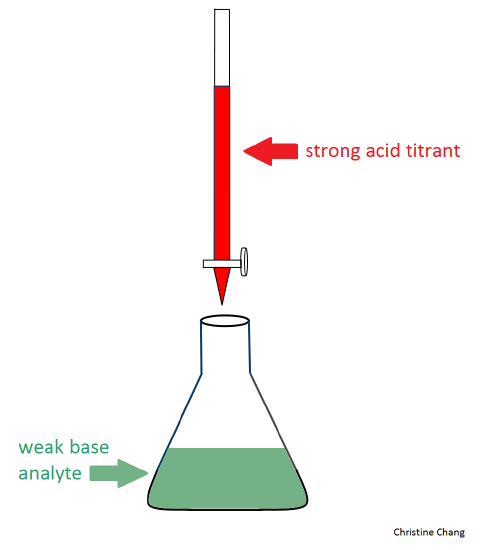
Before titrant is added
Before the stopcock on the buret containing the strong acid is released, the analyte in the flask is completely unreacted. Calculating the pH of this initial solution allows chemists to analyze the changes in acidity, as well as the acidic strength of the titrant after the titration is complete. To calculate the pH, an ICE (Initial, Change, Equilibrium) table is used. When titrating weak bases, water is always a reactant in this initial step, and its conjugate base, hydroxide, in the products.
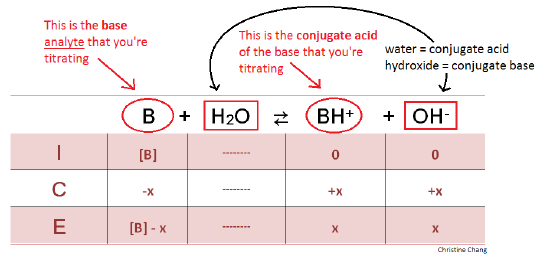
At this point, there is no BH+ or OH- in the analyte solution—the molarities of these species are zero, as observed in the ICE table. Because the stopcock has not yet been released, there is no acid in the flask to react with the base and yield products BH+ and OH-. Once the strong acid is released into the flask, however, the BH+ and OH- begin to form.
The next step in determining the initial concentration of OH- is to use the information from the ICE table to set up an equilibrium expression with Kb. Kb is used in this case, instead of Ka, because the analyte being titrated is a base.
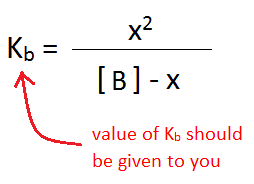
\({K_b} = {\dfrac{x^2}{[B] - x}}\)
Since Kb and [B] are given, the only variable left to solve for is x, which is equal to [OH-]. This requires the quadratic equation:
\(\dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)
Once x is obtained, the pOH can be determined using the relation \(pOH = -log x\). The pH can then be derived from the pOH using \(pH = 14 - pOH\).
At the midpoint
The midpoint is when the moles of strong acid added = ½ moles of base B initially in the flask. In other words, at the midpoint, half the analyte has been titrated. Because the number of moles of the base is known (determined by measured volume multiplied by molarity), and the molarities of both the titrant and analyte are known, the volumes of acid and base at the midpoint can be calculated as follows:
\(L \; strong \; acid = \dfrac{mol \; strong \; acid \; added}{Molarity \; strong \; acid}\)
or in simpler terms:
\(\dfrac{1}{M} = \dfrac{L}{mol}\), and \(L = mol{\dfrac{L}{mol}}\)
Graphically, the midpoint is the first point at which the curve has zero slope, indicated in Figure 2.
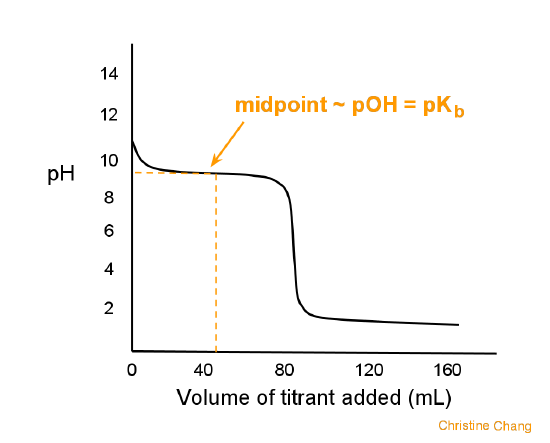
Lastly, at the midpoint, pOH = pKb. This makes it easy to calculate pH, because Kb is given.
Titrant added before the equivalence point
Chemists often calculate the acidity of the analyte at some point between the initial and the equivalence points to gauge the precise formation of the titration curve. Suppose 50 mL of 6 M strong acid is added to a base. Without looking at any graph, a chemist can determine whether or not he has passed the equivalence point.
The molarity of the acid is given, so the number of moles titrated can be calculated:
0.050 L × 6 mol/L = 0.3 moles of strong acid added thus far.
- If 0.3 < initial moles of base, the equivalence point has not yet been reached.
- If 0.3 = initial moles of base, the titration is at the equivalence point.
- If 0.3 > initial moles of base, the titration is past the equivalence point
If the equivalence point has not yet been reached, more acid is required. An ICE table is helpful in calculating the volume of B that has not been titrated at this point.

Notice that this time the variable x is not used, because the number of moles of titrant added is already known. Also note that the units are consistent across all values used in the ICE table. In an ICE table, either moles must be used for everything, or molarity for everything. Any inconsistency in units will result in incorrect values. The green ICE table above uses moles (the red ICE table in Step 1 used molarity).
Because there is no variable in the ICE table before the equivalence point, the Henderson-Hasselbalch equation can be directly applied to to find pOH.
\[pOH=pK_b+log\dfrac{[BH^+]}{[B]} \nonumber \]
Because the solution being titrated is a weak base, the pOH form of the Henderson Hasselbalch equation is used. If the analyte was an acid, however, this alternate form would have been used:
\[pH=pK_a+log\dfrac{[A^-]}{[HA]} \nonumber \]
The two should not be confused. The latter formula would likely be used in the titration of a weak acid with a strong base. If moles were used in the ICE table, as in the table above, the values must be converted to molarities before being inserted into the Henderson Hasselbalch equation. When converting to molarity, compute as follows:
\(Molarity \; BH^+ = {\dfrac{moles \; BH^+}{V_{titrant \; added} + V_{analyte}}}\)
The same must be done for base B. Do not forget the volume of titrant added in the denominator (liters of solution).
At the equivalence point
The equivalence point is defined as the point where the moles of strong acid added = initial moles of base B in solution. Graphically, the equivalence point is where the curve is most vertical.
At the equivalence point, an ICE table is required to determine volume and acidity. At this point in the titration, however, the reaction is flipped. This is because the base B has been fully titrated, which means adding more titrant will not yield the same products. The reaction goes backwards.
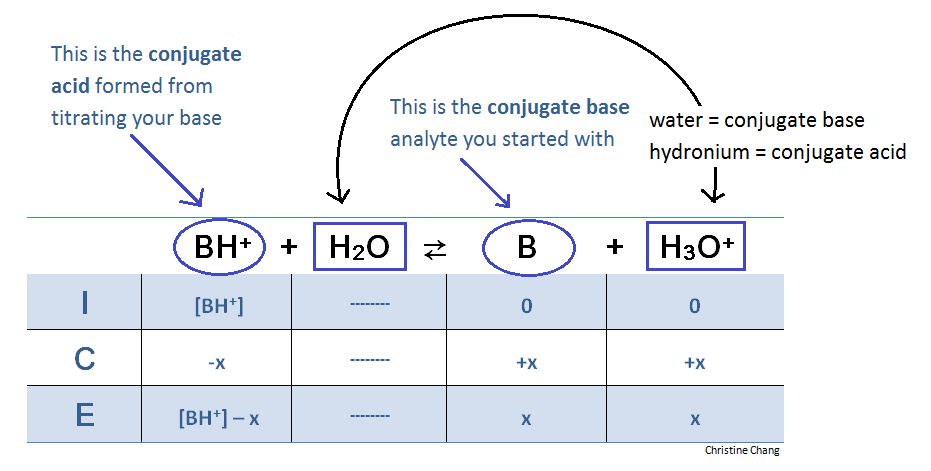
At the equivalence point, there is no more of base B. Hence, “reactant” is now considered the BH+ that formed from titrating B with strong acid. When calculating [BH+], do not forget to divide number of moles by the volume of base analyte PLUS TITRANT added.
Because the neutralization of the starting base is complete, the solution becomes increasingly acidic from this point on (as more acidic titrant is added. This is indicated by the hydronium in the product. Using an analogy, the titration can be thought of as a rising escalator. Once a person reaches the very top, or "equivalence point," he or she can only head back down in the opposite direciton. Likewise, at the equivalence point, the fully reacted reaction takes a "U-turn"—the former product becomes the reactant, and vice versa. Similar to step one, calculating the molarity of the products entails setting up an equilibrium expression with Ka (not Kb this time, because hydronium, which is acidic, is being produced instead of hydroxide, which is basic). Hint: Kb is given, and \( K_w = 1.0 \times 10^{-14} \)
\[ K_a = \dfrac{K_w}{K_b} \nonumber \]
Past the Equivalence Point
Suppose 100 mL of the 6 M strong acid titrant, which comes out to 0.6 moles, is added. If that number is greater than the number of moles of base B, the titration is past the equivalence point. To find the pH, first simply find the moles of excess H3O+. The excess can be calculated by subtracting initial moles of analyte B from moles of acidic titrant added, assuming a one-to-one stoichiometric ratio. Once the number of moles of excess H3O+ is determined, [H3O+] can be calculated.
\[ [\ce{H_3O^{+}}] = \dfrac{moles \; excess \; H_3O^+}{V_{titrant \; added} + V_{analyte}} \nonumber \]
The denominator (\({V_{titrant \; added} + V_{analyte}}\)) is the total volume of the solution in the flask.
Once the [H3O+] is determined, pH can be calculated with the knowledge that \(pH = -\log[\ce{H3O^{+}}]\).
You are given 90 mL of 0.6 M of the weak base \(\ce{NH3}\) (\(K_b = 1.8 \times 10^{-5}\)), and 1 M of the strong acid titrant HCl.
- What is the pH before any acid is added?
- What volume of acid (in mL) is needed to reach the equivalence (stoichiometric) point?
- What volume of acid (in mL) is needed to reach the halfway point where pH = pKa?
- What is the pH after 50 mL of acid is added?
- What is the pH at the equivalence (stoichiometric) point?
- What is the pH after 60 mL of acid is added?
Solution
First, calculate the number of moles of base (analyte) present initially.
\[0.090 \; L \; base \; \times \dfrac{0.6 \; mol \; base}{L \; base \; solution} = 0.054 \; mol \; base \nonumber \]
a) An ICE table helps determine the molarity of OH-.
| \(NH_3\) | \(H_2O\) | \(\rightleftharpoons\) | \(NH_4^+\) | \(OH^-\) | |
| Initial | 0.6 M | - | 0 | 0 | |
| Change | -x | - | +x | +x | |
| Equilibrium | 0.6 - x | - | x | x |
\[\begin{align*} 1.8 \times 10^{-5} &= \dfrac{x^2}{0.6 - x} \\[4pt] (1.08 \times 10^{-5}) - (1.8 \times 10^{-5})x - x^2 &= 0 \\[4pt] x &= \dfrac{1.8 \times 10^{-5} \pm \sqrt{(1.8 \times 10^{-5})^2 - 4(-1)(1.08 \times 10^{-5})}}{2(-1)} \\[4pt] &= \dfrac{1.8 \times 10^{-5} \pm 6.57 \times 10^{-3}}{-2} \end{align*}\]
The two solutions are thus \([\ce{OH^{-}}] = -3.29 \times 10^{-3}\) and \([\ce{OH^{-}}]= 3.28 \times 10^{-3} \; M \; OH^-\). The first one is meaningless, so from the second value we can calculate the pOH and pH:
\[pOH = -\log(3.28 \times 10^{-3}) = 2.5 \nonumber \]
\[pH = 14 - pOH = 14 - 2.5 = 11.5 \nonumber \]
b) At the equivalence point, the number of moles of \(\ce{HCl}\) added is equal to the initial number of moles of NH3, because the analyte is completely neutralized.
\[0.054 \; mol \; HCl \times \dfrac{1 \; L \; HCl}{mol \; HCl} = 0.054 \; L \; HCl, \; or \; 54 \; mL \; HCl \nonumber \]
c) At the midpoint, pOH = pKb.
\(-\log(1.8 \times 10^{-5}) = 4.74 \; pOH\)
\(pH = 14 - pOH = 14 - 4.74 = 9.26 \; pH\)
At the midpoint, the number of moles of HCl added equals half the initial number of moles of NH3. In other words, the number of moles of HCl added at the midpoint is half of the number of moles of HCl added by the equivalence point. Hence:
\[\dfrac{1}{2}(0.054 \; L \; HCl \; added \; at \; equivalence \; point) = 0.027 \; moles \; HCl \; at \; midpoint \nonumber \]
\[\text{Volume of acid needed} = 0.027\ mol\ HCl \times \dfrac{1\ L}{1\ mol\ HCl} = 0.027\ L\ HCl = 27\ mL\ HCl \nonumber \]
d) First, find the moles of HCl in 50 mL of HCl.
\[0.05 \; L \; HCl \times \dfrac{mol \; HCl}{L \; HCl} = 0.05 \; mol \; HCl \nonumber \]
| \(NH_3\) | \(H_2O\) | \(\rightleftharpoons\) | \(NH_4^+\) | \(OH^-\) | |
| Initial | 0.054 mol | - | 0 | 0 | |
| Change | -0.050 mol | - | +0.050 mol | +0.050 mol | |
| Equilibrium | 0.004 mol | - | 0.050 mol | 0.050 mol |
Because 50 mL of acid have been added, and we started out with 90 mL of analyte, there are a total of 140 mL of analyte solution at this point. Hence, the molarity of NH3 is the following:
\(\dfrac{0.004 \; mol \; NH_3}{0.140 \; L \; solution \; in \; flask}=0.0286 M\)
The molarity of NH4+ is:
\(\dfrac{0.050 \; mol \; NH_4^{+}}{0.140 \; L \; solution \; in \; flask}=0.357 M\)
Now we can use the Henderson-Hasselbalch approximation:
\(pOH=pK_b+log\dfrac{NH_4^{+}}{NH_3}\)
\(pOH=4.74+log\dfrac{0.357}{0.0286}=5.84 \; pOH\)
\(pH=14-pOH=14-4.84=8.16\)
e) To find the pH at the equivalence point, first calculate the molarity of the NH4+ in the flask at this point.
\(\dfrac{0.054 \; mol \; NH_4{^+}}{0.140 \; L \; analyte \; solution}=0.375M \; NH_4{^+}\)
\(K_a=\dfrac{K_w}{K_b}=\dfrac{1.0 \times 10^{-14}}{1.8 \times 10^{-5}}=5.56 \times 10^-10\)
| \(NH_4^+\) | \(H_2O\) | \(\rightleftharpoons\) | \(NH_3\) | \(H_3O^+\) | |
| Initial | 0.375 | -- | 0 | 0 | |
| Change | -x | -- | +x | +x | |
| Equilibrium | 0.375 -x | -- | x | x |
\(5.56 \times 10^{-10}=\dfrac{x^2}{0.375+x}\)
\(2.09 \times 10^{-10}+(5.56 \times 10^{-10})x-x^2=0\)
We can use the quadratic equation to solve for x:
\(x=\dfrac{-5.56 \times 10^{-10} \pm \sqrt{(5.56 \times 10^{-10})^2-4(-1)(2.09 \times 10^{-10})}}{2(-1)}\)
\(=\dfrac{-5.56 \times 10^{-10} \pm 2.89 \times 10^{-5}}{-2} = -1.45 \times 10^{-5}, \; 1.45 \times 10^{-5} \; M \; H_3O^+\)
\(pH=-log(1.45 \times 10^{-5})=4.84 \; pH\)
f) First, find the moles of HCl in 60 mL of HCl.
\(0.06 \; L \times \dfrac{mol\; HCl}{L \; HCl}=0.06 \; mol \; OH^-\)
Find the excess amount of HCl, or the amount added after neutralization has occurred.
0.054 moles of HCl reacted with the NH3 to neutralize it.
\(excess \; HCl=0.06-0.054=0.006 \; mol \; HCl\)
Now we need to find the molarity of HCl in the flask at this point. We started out with 90 mL of NH3 analyte in the flask, and added 60 mL. That gives a total of 150 mL, or 0.150 L of solution in the flask.
\(MOLARITY_{HCl \; in \; flask}=\dfrac{0.006 \; mol}{0.150 \; L \; solution}=0.04 \; M \; HCl\)
Because HCl dissociates into H3O+, equate [HCl] to [H3O+]. Now we have the information to determine pH.
\(pH=-log(0.04)=1.4 \; pH\)
One titrates 100 ml of 1.00 M sodium chlorate(NaClO) with 1.00M HCl. What is the pH after you add 50 ml of acid? Kb for ClO- = 3.6×10-7.
Solution
Two main steps
- Do the stoichiometry to find how much base has been absorbed by the acid.
- Figure out the equilibrium concentrations of each species by doing an equilibrium problem.
Reaction of weak base and strong acid.
\[\ce{H^{+}(aq) + ClO^{-}(aq) -> HClO(aq)} \nonumber\]
- Start with 100 ml(1.00 M) = 0.100 moles of ClO-.
- If you add 50ml(1.00 M) = 0.05 moles of HCl to the base, the reaction in the previous step will consume all of the H+, leaving 0.100 - 0.050 = 0.050 moles of ClO-.
- Because we added 50 ml of acid to 100 ml of base, we have a solution volume of 150 ml.
- The concentration of ClO- after adding the base is [ClO-] = 0.050 moles/0.150 L = 0.333 M.
- 0.050 moles of HClO also forms, thus the concentration of HClO is also 0.333 M.
- The solution above is a buffer of the weak acid HClO and the conjugate base ClO-.
- Now we can solve for the pH of a buffer by using the Henderson-Hasselbalch approximation.

